常见的信号检测算法一般包括以下几类检测算法:最优、线性和非线性。
最优检测算法:最大似然算法
线性检测算法:迫零检测算法和最小均方误差检测算法
非线性检测算法:串行干扰消除检测算法
球形译码检测算法属于一种次优检测算法(运算量远小于最大似然检测算法)
作为一种性能接近ML的次优算法,球形译码(SD)可以大大降低检测的复杂度。简单来说,SD就是在限制为球形的多维搜索空间中找到一个距离接收矢量最近的发射星座矢量。球形译码检测算法的复杂度与天线数目和调制阶数成指数关系,并且与信噪比成反比关系。那么实际上这是一种硬判决,不能产生输入给译码器的软信息。硬判决的好处是译码复杂度低且对信道估计误差不敏感。
信号检测:发射端以多个天线进行发射信号,发射信号经过无线信道后到达接收端,在接收端的每个天线接收了所有的信号,而不是发射信号,因而要恢复发射信号需要进行信号检测算法。这样信号检测就成为了物理层链路不可缺少的部分,而信号检测算法是信号检测的核心,那么整个物理链路的质量的好坏将取决于信号检测算法性能好坏。
最大似然检测算法——ML
先用过比较接收到的信号向量和发射的信号向量的全部可能值,再由最大似然准则来对发射信号的向量x进行计算。

迫零检测算法——ZF
ZF算法是一种最小二乘估计的最简单的线性检测算法,其基本思想就是通过滤波矩阵对接收的信号向量y进行滤波,来达到完全消除多个天线发送的符号间干扰的目的。迫零检测算法在抑制发送符号间干扰的同时很容易过度放大了被检测信号的噪声,最终使判决结果产生误差。


串行干扰消除检测算法——SIC
串行干扰消除检测算法是一种垂直分层空时(V-BLAST)检测算法。在检测时,它不是直接从接收信号向量中检测发射信号向量,而是按顺序从第一个或者最后一个向量的分量进行检测,完成一次检测后得出的信号分量就马上脱离接收信号向量,不再对接收信号向量产生任何影响,然后逐次检测剩余的信号分量,从而使待检测信号向量的干扰量减少,检测的可靠性提高。
SIC检测算法的基本思想是在检测过程中对发射信号向量进行一层一层的检测和消除,其通过迭代的处理来完成了检测。SIC检测算法在检测过程中的每一级递归分为两个主要的操作步骤。零化和干扰消除。
最小均方误差检测算法——MMSE
最小均方误差检测算法的基本思想就是通过设计一个滤波矩阵来达到发送信号x的实际值与估计值之间的均方误差最小,它是基于ZF检测算法噪声增强问题而提出的检测算法,其降低了噪声的影响,从而提高检测的性能。随着噪声功率增大,MMSE检测算法的性能相对ZF检测算法的性能越好。由于MMSE检测算法同ZF检测算法一样是线性检测算法,性能方面还是不特别的理想,但是算法复杂度低,易实现,可以应用到实际中。


球形译码检测算法——SD
SD的思想非常简单:在经过信道扭曲的栅格空间中,以接收矢量y为球心,做一个设定的半径球,通过只搜索超球体中的栅格点来减小搜索空间和所需的计算量。很明显,在球中离y最近的栅格点也是整个空间离y最近的栅格点。
可以对半径进行设定和改变来使这个多维球包含的空间减少,这样搜索的点数量减少,最终算法的计算复杂度变低。从中可以看出,格点在这个多维球内的且与矢量的距离最近,那么这个格点为要找到的点即最大似然值。这种检测算法与最大似然检测算法不同之处在于,它不需要对全部的格点进行搜索,而仅仅在一个半径确定的球内展开搜索,可见搜索区域较最大似然检测算法明显减少,这样搜索的时间就大大缩减了。
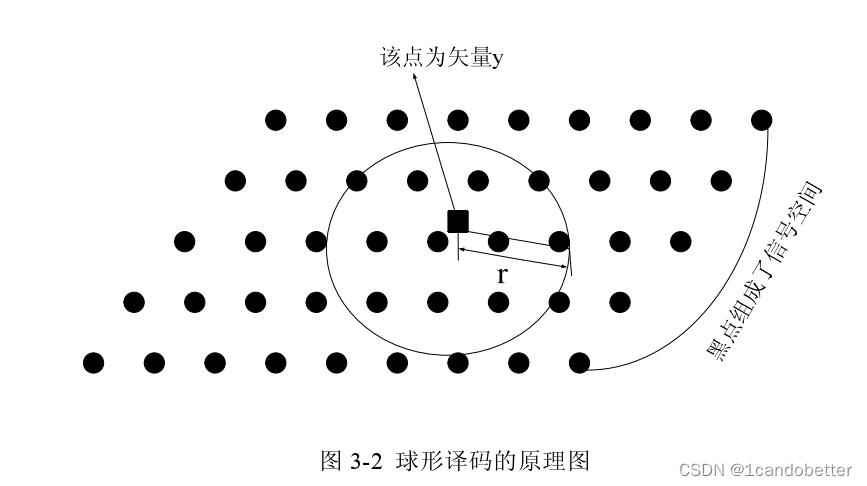

初始的搜索半径的确定和球内是否存在有效点的确定是影响球形译码检测算法的性能的两个因素:
(1)初始半径的设置
若太大,那么球的体积大,球内包含点多,计算复杂度很大
若太小,球内可能不存在最大似然点,从而需要重新检测,因而上次检测失败
为了减少搜索空间,SD选出一个合适的值来作为球形搜索域的半径(r^2=C),目标就是要找出球中具有最小权值的栅格点。H可以被QR分解成酉矩阵Q和上三角阵R的乘积。
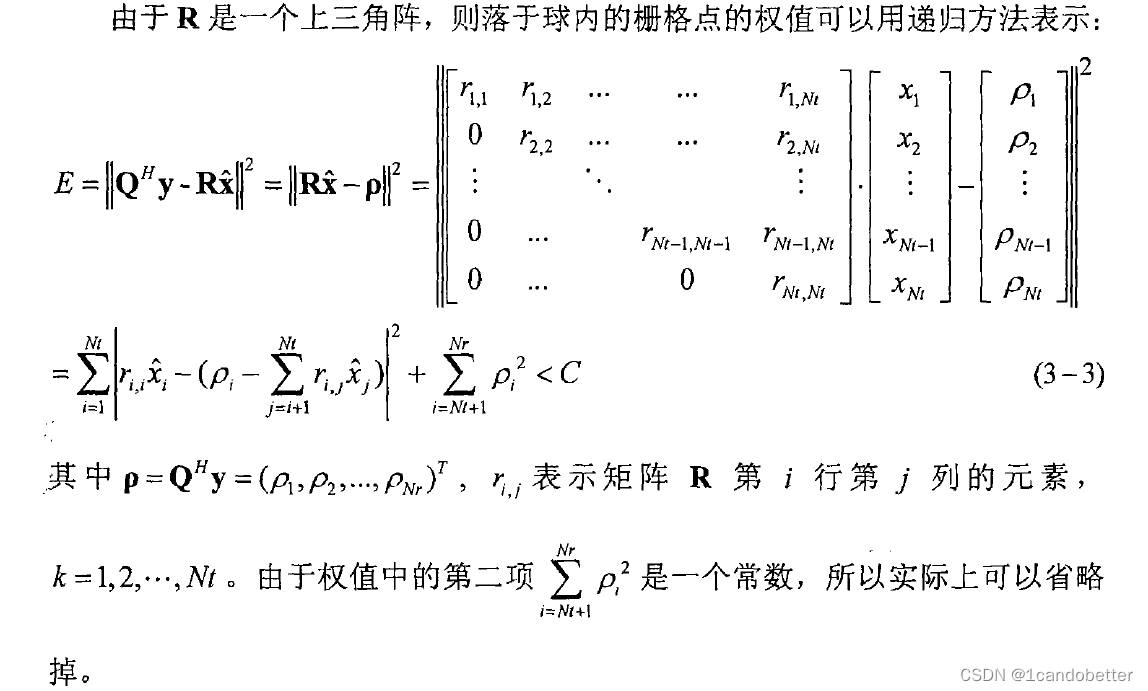

(2)球内是否存在有效点的确定
如果每次判断对该点是否于球内都要计算该点和矢量之间的距离的话,那么这个计算量也是指数级的。
球形译码算法根据格点搜索的方式不同,可以分为V-B球形译码和C-L球形译码。
V-B球形译码
F-P搜索方法与ML检测相结合。目的是搜索到一个在区域球内的全部点的序列。

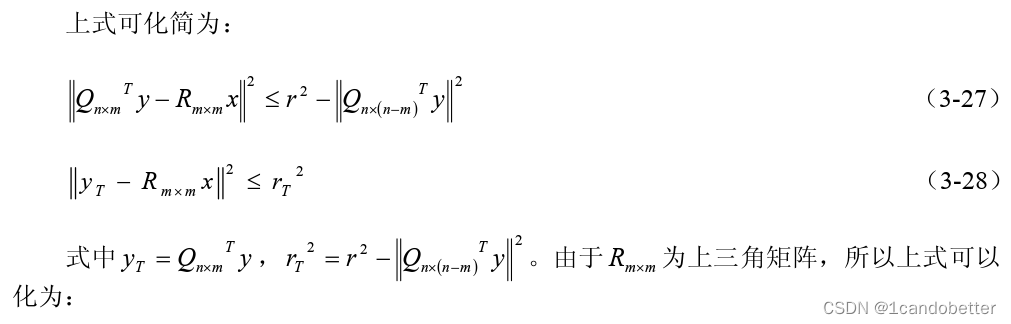

C-L球形译码算法

在C-L球形译码算法中,如果球的半径设置无穷大,那么在这个球内总能找到点,而且首先搜索到的点是迫零反馈均衡点。
C-L球形译码算法的优点在于:该算法的第一个搜索点是最小化分支度量的一个替补节点,这样搜索的方向提前进行了更正;当没有搜索到点时,就不会再去对该层其他余下的节点进行搜索,大大减少了算法;由于初始晶格点是不变的,该算法可以自由选择初始半径,而且当信噪比较高时,其搜索效果比较好。
参考《LTE系统信号检测算法的研究》尹鑫