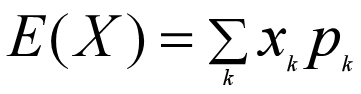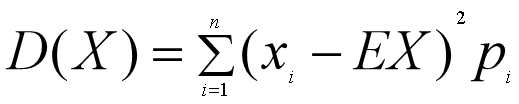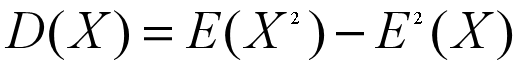文章目录
- 基本统计分析
- 1基本方法
- summary()函数
- apply()函数
- lapply()函数
- sapply()函数
- 2.常见的描述指标
- 标准误
- binom.test (二项分布精确检验)
- 变异系数
- 极差
- 偏度系数(skewness)
- 3分组计算描述性统计量
- aggregate()函数
- by()函数
- 频数表和列联表
- 列联表
- 生成频数表
- 一维列联表
- 二维列联表
- 3多维列联表
- 非参数检验
- 假设检验(Hypothesis Testing)
- 符号检验
- 符号秩检验与秩和检验
- Wilcoxon符号秩检验 (Wilcoxon signed-rank test)
- Wilcoxon秩和检验
- 独立性检验
- Pearson(皮尔逊)卡方检验
- Fisher精确独立性检验
- 分布的检验
- Pearson拟合优度卡方检验
- 单样本泊松分布总体的均值检验(Poisson)
- 相关性检验
- Pearson(皮尔逊)相关检验
- Spearman秩相关检验
- Kendall(肯德尔)相关检验
- 总结
- 习题
基本统计分析
统计分析:分为统计描述和统计推断两部分。统计描述是通过绘制统计图、编制统计表、计算统计量等方法来表述数据的分布特征。
| mpg | 每加仑汽油行驶英里数 |
|---|---|
| wt | 车重 |
| am | 变速箱类型,0 自动挡 1 手动挡 |
| cyl | 气缸数 |
> myvars<-c("mpg","hp","wt")
> head(mtcars[myvars])
mpg hp wt
Mazda RX4 21.0 110 2.620
Mazda RX4 Wag 21.0 110 2.875
Datsun 710 22.8 93 2.320
Hornet 4 Drive 21.4 110 3.215
Hornet Sportabout 18.7 175 3.440
Valiant 18.1 105 3.460
mtcars数据集来源于Motor Trend杂志的车辆路试数据集,head(dataframe)查看数据集前6行数据
1基本方法
summary()函数
> myvars<-c("mpg","hp","wt")
> summary(mtcars[myvars])
mpg hp wt
Min. :10.40 Min. : 52.0 Min. :1.513
1st Qu.:15.43 1st Qu.: 96.5 1st Qu.:2.581
Median :19.20 Median :123.0 Median :3.325
Mean :20.09 Mean :146.7 Mean :3.217
3rd Qu.:22.80 3rd Qu.:180.0 3rd Qu.:3.610
Max. :33.90 Max. :335.0 Max. :5.424
apply()函数
apply(X, MARGIN, FUN)
参数说明:
- -x: 一个数组或者矩阵
- -MARGIN: 两种数值1或者2决定对哪一个维度进行函数计算
- -MARGIN=1
: 操作基于行-MARGIN=2: 操作基于列 - -MARGIN=c(1,2)`: 对行和列都进行操作
- -FUN: 使用哪种操作,内置的函数有mean(平均值)、medium(中位数)、sum(求和)、min(最小值)、max(最大值),当然还包括广大的用户自定义函数
例题
> m1<-matrix(c<-(1:10),nrow=5,ncol=6)
> m1
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 6 1 6 1 6
[2,] 2 7 2 7 2 7
[3,] 3 8 3 8 3 8
[4,] 4 9 4 9 4 9
[5,] 5 10 5 10 5 10
> a_m1<-apply(m1,2,sum)#使用sum函数对列求和
> a_m1
[1] 15 40 15 40 15 40
> f_m1<-apply(m1,2,function(x)x*2)#使用自定义函数
> f_m1
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 2 12 2 12 2 12
[2,] 4 14 4 14 4 14
[3,] 6 16 6 16 6 16
[4,] 8 18 8 18 8 18
[5,] 10 20 10 20 10 20
lapply()函数
lapply()函数中多出来的l代表的是list,所以lapply()和apply()的区别在于输出的格式,lapply()的输出是一个列表(list),所以lapply()函数不需要MARGIN参数。
> mydata<-c(1:3)
> lapply(mydata,function(x) x*3)
[[1]]
[1] 3
[[2]]
[1] 6
[[3]]
[1] 9
> unlist( lapply(mydata,function(x) x*3))
[1] 3 6 9
unlist函数用于去列表化,将list转为向量
sapply()函数
sapply()和lapply()这两个函数的功能和用法比较相似,作用于如向量或列表的数据集合上。
> mydata<-c(1:3)
> sapply(mydata,function(x) x*3)
[1] 3 6 9
在sapply函数的参数中添加 simplify=FALSE 即可使函数结果为list格式
> sapply(mydata,function(x) x*3,simplify=FALSE)
[[1]]
[1] 3
[[2]]
[1] 6
[[3]]
[1] 9
mystats<-function(x,na.omit=FALSE){
if(na.omit)
x<-x[!is.na(x)]
m<-mean(x)
n<-length(x)
s<-sd(x)
skew<-sum((x-m)^3/s^3)/n
kurt<-sum((x-m)^4/s^4)/n-3
return(c(n=n,mean=m,stdev=s,skew=skew,kurtosis=kurt))
}
myvars<-c("mpg","hp","wt")
sapply(mtcars[myvars],mystats)

2.常见的描述指标
最小值(Min):样本的最小值
最大值(Max):样本的最大值
平均值(Mean):数据的平均得分值,反映数据的集中趋势
标准差(Standard Deviation, SD/Std/Std.Deviation):反映数据的离散程度
中位数(Median):样本数据升序排列后的最中间的数值,如果数据偏离较大,一般用中位数描述整体水平情况,而不是平均值
25分位数:分析项中所有数据由大到小排列后的第25%的数字,用于了解部分样本占总体样本的比例
75分位数:分析项中所有数值由大到小排列后的第75%数字
IQR(Interquartile Range):四分位距IQR=75分位数-25分位数
方差(Variance):用于计算每个变量(观察值)与总体均值之间的差异
标准误(Standard Error,SE):样本均数的标准差,反映样本数据的离散趋势
峰度(Kurtosis):反映数据分布的平坦度,通常用于判断数据正态性情况
偏度(skewness):反映数据分布偏斜方向和程度,通常用于判断数据正态性情况
变异系数(Coefficient of variation,C.V.):标准差除以平均值,表示数据沿着平均值波动的幅度比例,反映数据的离散趋势
标准误
标准误(Standard Error,SE)或者 SEM(Standard Error of Mean)
定义:即样本均数的标准差,可用于衡量抽样误差的大小。
意义:反映样本均数间离散程度。标准误越小,抽样误差越小,用样本均数估计总体均数的可靠性越大。

样本均数也称样本均值,样本均值(sample mean)又叫样本均数。即为样本的均值。均值是表示一组数据集中趋势的量数,是指在一组数据中所有数据之和再除以这组数据的个数。它是反映数据集中趋势的一项指标。
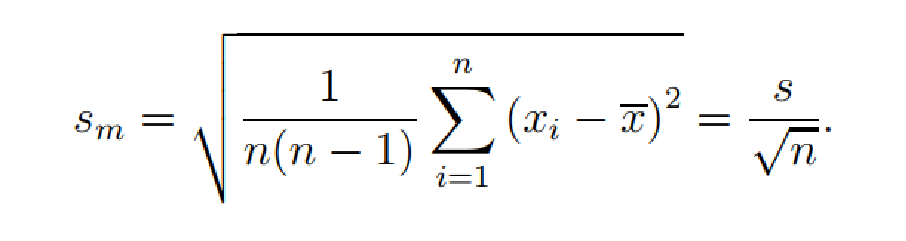
有plotrix软件包有一个内置函数:std.error

为什么要有标准误?
大部分研究的目的是估计某个总体(population)的参数,比如均值和SD(标准方差)。一旦有了估计值,另外一个问题随之而来:这个估计的精确程度如何?我们实际上不知道确切的总体参数值,所以怎么能评价估计值的接近程度呢?我们可以求助于概率:(问题转化成)真实总体均值处于某个范围内的概率有多大?(格言:统计意味着你不需要把话给说绝了。)
但是首先得处理一个小纰漏:重复研究(实验)几百次。现今做一次研究已经很困难了,不要说几百次了(即使你能花费整个余生来做这些实验)。好在一向给力的统计学家们已经想出了基于单项研究(实验)确定SE的方法。
让我们先从直观的角度来讲:是哪些因素影响了我们对估计精确性的判断?一个明显的因素是研究的规模。样本规模N越大,反常数据对结果的影响就越小,我们的估计就越接近总体的均值。所以,N应该出现在计算SE公式的分母中:因为N越大,SE越小。类似的,第二因素是:数据的波动越小,我们越相信均值估计能精确反映它们。所以,SD应该出现在计算公式的分子上:SD越大,SE越大。
SD和SE的差别
标准误:反映抽样误差,用于对总体均数、置信区间进行统计学检验。
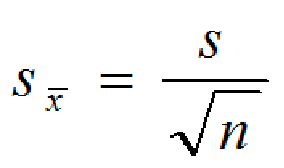
标准差:反映个体变异,用于计算参考值范围、计算标准误、CV。
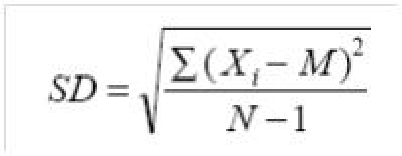
总之:SD 实际上反映的是数据点的波动情况,而 SE 则是均值的波动情况。
标准差越大,说明个体差异越大。
样本均值(sample mean)又叫样本均数。即为样本的均值。均值是表示一组数据集中趋势的量数,是指在一组数据中所有数据之和再除以这组数据的个数。它是反映数据集中趋势的一项指标。标准误是表示均数抽样误差的指标,标准误大抽样误差大。用标准误大的样本均数估计总体均数不可靠。
binom.test (二项分布精确检验)
Description: Performs an exact test of a simple null hypothesis about the probability of success in a Bernoulli experiment.
Usage:
binom.test(x, n, p = 0.5,alternative = c("two.sided", "less", "greater"),conf.level = 0.95)
Parameter:
x:成功的数量,或长度为2的向量,分别给出成功和失败的数量。
n:试验的次数
p:假设的成功概率
alternative:表示备择假设
对伯努利实验成功概率的一个简单的零假设进行精确的检验。
变异系数
变异系数(Coefficient of Variation,CV):又称“离散系数”,是概率分布离散程度的一个归一化量度,其定义为标准差与平均值之比:
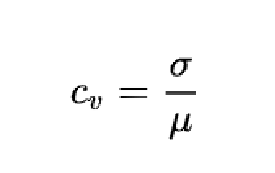
变异系数(coefficient of variation)只在平均值不为零时有定义,而且一般适用于平均值大于零的情况。变异系数也被称为标准离差率或单位风险。
变异系数越小,变异程度越小。
原因:变异系数为不同单位的几个指标之间比较变异程度时的参考指标,变异系数越大,表示变异程度越大。
变异系数当需要比较两组数据离散程度大小的时候,如果两组数据的测量尺度相差太大,或者数据量纲的不同,直接使用标准差来进行比较不合适,此时就应当消除测量尺度和量纲的影响。
优点:比起标准差来,变异系数的好处是不需要参照数据的平均值。变异系数是一个无量纲量,因此在比较两组量纲不同或均值不同的数据时,应该用变异系数而不是标准差来作为比较的参考。
缺陷:
- 当平均值接近于0的时候,微小的扰动也会对变异系数产生巨大影响,因此造成精确度不足。
- 变异系数无法发展出类似于均值的置信区间的工具。
极差
又称范围误差或全距(Range),以R表示。是用来表示统计资料中的变异量数(measures of variation)
R = x(n) − x(1) = max(x) − min(x)
它是标志值变动的最大范围,它是测定标志变动的最简单的指标
偏度系数(skewness)
定义:是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。
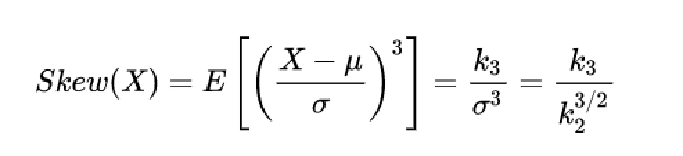
其中 k2和k3 分别表示样本的二阶和三阶中心矩。
说明:偏度系数是刻划数据的对称性指标。关于均值对称的数据其偏度系数为0,右侧更分散的数据偏度系数为正,左侧更分散的数据,偏度系数为负。
3分组计算描述性统计量
aggregate()函数
aggregate(x, by, FUN, ..., simplify = TRUE)
函数功能:首先将数据按行进行分组,然后对每一组数据进行函数统计,最后把结果整合成一个表格返回。
> myvars<-c("mpg","hp","wt")
> aggregate(mtcars[myvars],by=list(am=mtcars$am),mean)
am mpg hp wt
1 0 17.14737 160.2632 3.768895
2 1 24.39231 126.8462 2.411000
by参数也可以包含多个类型的因子,得到的就是每个不同因子组合的统计结果
> aggregate(mtcars[myvars],by=list(am=mtcars$am,cyl=mtcars$cyl),mean)
am cyl mpg hp wt
1 0 4 22.90000 84.66667 2.935000
2 1 4 28.07500 81.87500 2.042250
3 0 6 19.12500 115.25000 3.388750
4 1 6 20.56667 131.66667 2.755000
5 0 8 15.05000 194.16667 4.104083
6 1 8 15.40000 299.50000 3.370000
注意:list(am=mtcars$am)的使用,目的是创建新的列标签而不采用默认的标签
by()函数
使用by()分组计算描述性统计量
by(data,INDICES,FUN)
其中:
- data是一个数据框或者矩阵
- INDICES是一个因子或因子组成的列表,定义了分组
- FUN为任意的函数
> dstats<-function(x) sapply(x,mystats)
> myvars<-c("mpg","hp","wt")
> by(mtcars[myvars],mtcars$am,dstats)
mtcars$am: 0
mpg hp wt
n 19.00000000 19.00000000 19.0000000
mean 17.14736842 160.26315789 3.7688947
stdev 3.83396639 53.90819573 0.7774001
skew 0.01395038 -0.01422519 0.9759294
kurtosis -0.80317826 -1.20969733 0.1415676
---------------------------------------------------------------
mtcars$am: 1
mpg hp wt
n 13.00000000 13.0000000 13.0000000
mean 24.39230769 126.8461538 2.4110000
stdev 6.16650381 84.0623243 0.6169816
skew 0.05256118 1.3598859 0.2103128
kurtosis -1.45535200 0.5634635 -1.1737358
频数表和列联表
定性数据:描述的数值方法常用频数或者相对频率来刻画。
列联表
列联表(contingency table)又称交互分类表,所谓交互分类,是指同时依据两个变量的值,将所研究的个案分类。交互分类的目的是将两变量分组,然后比较各组的分布状况,以寻找变量间的关系。
特征1
观测数据按两个或更多属性(定性变量)分类时所列出的频数表。 例如,对随机抽取的1000人按性别(男或女)及色觉(正常或色盲)两个属性分类,得到二行二列的列联表,又称2×2表或四格表。
特征2
一般,若总体中的个体可按两个属性A与B分类,A有r个等级A1,A2,…,Ar;B有с个等级B1,B2,…,Bc,从总体中抽取大小为n的样本设其中有nij个属于等级Ai和Bj,nij称为频数,将r×с个nij(i=1,2,…,r;j=1,2,…,с)排列为一个r行с列的二维列联表,简称r×с表。
特征3
若所考虑的属性多于两个,也可按类似的方式作出列联表,称为多维列联表。由于属性或定性变量的取值是离散的,因此多维列联表分析属于离散多元分析的范畴,列联表分析在应用统计,特别在医学、生物学及社会科学中,有重要的应用。
生成频数表
频数分布表(frequency distribution table)是对类别数据(因子的水平)计数或数值数据类别化(分组)后计数生成的表格。
频 数:对于给定的类,落入该类中观测值的个数。
相对频率:落入给定类中观测值个数相对于观测值总数的比例。
一维列联表
R语言生成列联表的函数:base包中的table函数,stats包中的ftable函数,vcd包中的structable函数等。

百分比表

例题 vcd包中的Arthritis数据集,表示了一项风湿性关节炎新疗法的双盲临床实验结果。
with表示把操作限定在括号中的数据集上
> mytable<-with(Arthritis,table(Improved))
> mytable
Improved
None Some Marked
42 14 28
> a<-table(Improved=Arthritis$Improved)
> attach(Arthritis)
> table(Improved)
Improved
None Some Marked
42 14 28
detach(Arthritis)
二维列联表
二维列联表(Two dimensional contingency table)或 交叉表 (cross table)当涉及两个类别变量时,可以将一个变量的各类别放在“行”的位置,另一个变量的各类别放在“列”的位置(行和列可以互换),由两个类别变量交叉分类形成的频数分布表称为二维列联表。
例题 (数据 data1_1.csv) 以性别和满意度为例,生成二维列联表

Addmargins为列联表添加边际和
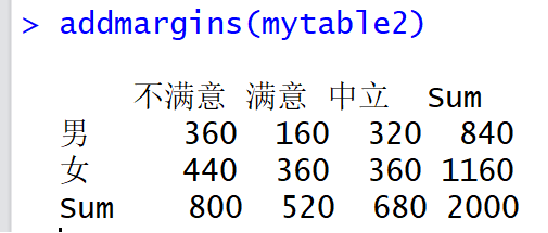
使用xtabs

行和与行比例
> margin.table(mytable,1)
Treatment
Placebo Treated
43 41
> prop.table(mytable,1)
Improved
Treatment None Some Marked
Placebo 0.6744186 0.1627907 0.1627907
Treated 0.3170732 0.1707317 0.5121951
结论: 与接受安慰剂的个体中有明显改善的16%相比,接受治疗的个体中的51%病情有了明显的改善。
列和与列比例
> margin.table(mytable,2)
Improved
None Some Marked
42 14 28
> prop.table(mytable,2)
Improved
Treatment None Some Marked
Placebo 0.6904762 0.5000000 0.2500000
Treated 0.3095238 0.5000000 0.7500000
各单元格所占比例
> margin.table(mytable)
[1] 84
> > prop.table(mytable)
Improved
Treatment None Some Marked
Placebo 0.34523810 0.08333333 0.08333333
Treated 0.15476190 0.08333333 0.25000000
不加行和列信息,就是求得整个占比情况
为表格添加边际和
> addmargins(mytable)
Improved
Treatment None Some Marked Sum
Placebo 29 7 7 43
Treated 13 7 21 41
Sum 42 14 28 84
> addmargins(prop.table(mytable))
Improved
Treatment None Some Marked Sum
Placebo 0.35 0.08 0.08 0.51
Treated 0.15 0.08 0.25 0.49
Sum 0.50 0.17 0.33 1.00
为表中所有变量创建边际和
> addmargins(prop.table(mytable,1),2)
Improved
Treatment None Some Marked Sum
Placebo 0.67 0.16 0.16 1.00
Treated 0.32 0.17 0.51 1.00
> addmargins(prop.table(mytable,2),1)
Improved
Treatment None Some Marked
Placebo 0.69 0.50 0.25
Treated 0.31 0.50 0.75
Sum 1.00 1.00 1.00
3多维列联表
xtabs
> mytable<-xtabs(~Treatment+Sex+Improved,data=Arthritis)
> mytable
, , Improved = None
Sex
Treatment Female Male
Placebo 19 10
Treated 6 7
, , Improved = Some
Sex
Treatment Female Male
Placebo 7 0
Treated 5 2
ftable
> ftable(mytable)
Improved None Some Marked
Treatment Sex
Placebo Female 19 7 6
Male 10 0 1
Treated Female 6 5 16
Male 7 2 5
>ftable(prop.table(mytable,c(1,2)))
Improved None Some Marked
Treatment Sex
Placebo Female 0.59 0.22 0.19
Male 0.91 0.00 0.09
Treated Female 0.22 0.19 0.59
Male 0.50 0.14 0.36
ftable(addmargins(prop.table(mytable,c(1,2)),3))
Improved None Some Marked Sum
Treatment Sex
Placebo Female 0.59 0.22 0.19 1.00
Male 0.91 0.00 0.09 1.00
Treated Female 0.22 0.19 0.59 1.00
Male 0.50 0.14 0.36 1.00
非参数检验
导入案例:
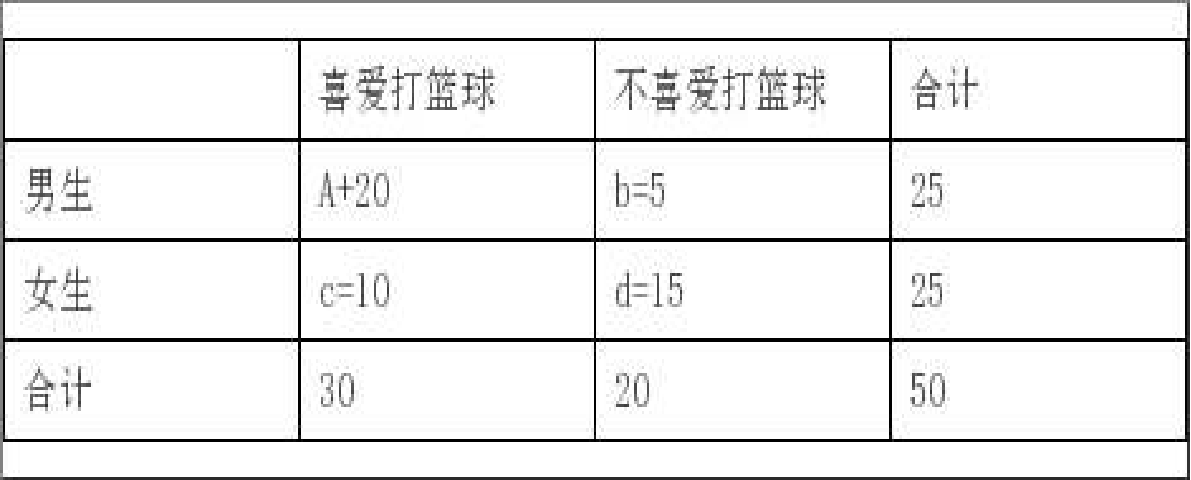
某大学的人事处,为学校招聘青年教师,人事处共收到80位男生和60位女生的应聘申请,结果聘用了35名男生和20名女生。
某媒体得知后,以“大学招聘歧视女生”为题做了报道,其理由是:在该大学的招聘结果中,男生被聘用的比例是35/80=43.75%,而女生被聘用的比例是20/60=33.33%,只有1/3.
该大学人事处马上在网上做出了回应,声称在招聘过程中没有歧视女生,并列出招聘结果细节。无论是电机工程系还是外语系,男女生被聘用的比例是相同的,分别都是50%和25%。

问题:该大学在招聘中是否存在性别歧视呢?
参数检验和非参数检验的区别是什么?
参数检验:假定数据服从某分布(一般为正态分布),通过样本参数的估计量( μ ±var)对总体参数进行检验,比如t检验、u检验、方差分析。
非参数检验:不需要假定总体分布形式,直接对数据的分布进行检验。由于不涉及总体分布的参数,故名「非参数」检验。比如,卡方检验。
参数检验的集中趋势的衡量为均值,而非参数检验为中位数。
参数检验需要关于总体分布的信息;非参数检验不需要关于总体的信息。
测量两个定量变量之间的相关程度,参数检验用Pearson相关系数,非参数检验用Spearman秩相关。
简而言之,若可以假定样本数据来自具有特定分布的总体,则使用参数检验。如果不能对数据集作出必要的假设,则使用非参数检验。
假设检验(Hypothesis Testing)
假设检验(Hypothesis Testing)是数理统计学中根据一定假设条件由样本推断总体的一种方法。
原假设:没有发生; 如:变量不是独立的,没有中奖,药物治疗没有效果,
备择假设:发生了;如:变量是独立的,中奖了,药物治疗有效果
P-value就是Probability的值,是一个通过计算得到的概率值,也就是在原假设为真时,得到最大的或者超出所得到的检验统计量值的概率。
一般将置信区间设置为5%,当得到的p值<0.05,拒绝原假设,否则,接收原假设。(p-value越小,说明原假设越不靠谱;p-value越大,说明原假设越靠谱。)
假设检验中,如何提出原假设?
你想要证明的就是备择假设,与之矛盾的就是原假设H0。
假设检验是倾向于保护原假设的。
比如说要推广一种新药,如果原假设是该药可靠,那只有很不可靠的时候才会拒绝。但若原假设是该药不可靠,只有很可靠的时候才会拒绝。在这个具体问题中,推广新药必须要很可靠才行,所以一般会把原假设定为该药不可靠。再说仔细一些,一般取置信区间为0.05,也就是说只有当原假设前提下5%的小概率事件发生时,才会拒绝原假设。
我们常把没有充分理由不能轻易否定的命题作为原假设H0,而常把没有把握不能轻易肯定的命题作为备择假设H1.
假设检验通常是通过拒绝原假设,来以较大的概率接受备择假设。如果置信区间设为95,则可以说有95%的概率认为备择假设是可以接受的。
比如:某装置的平均工作温度据制造厂家称低于190,今从一个由16台装置构成的随机样本测得工作温度的平均值和标准差分别为195和8,根据这些数据能否支持厂家结论?设α=0.05,并假设工作温度近似服从正态分布。
按照题意来选择原假设与备择假设。如果我是生产厂商,我肯定希望选择对自己有利的假设,而u<190可以保证我的产品的样本统计值即使超出这个温度一定范围内仍然可以被通过,这实际上是对本产品放松了检验要求。
如果我是经销商我希望得到更好质量的产品,我希望严格检验要求,选择u>190为原假设,这样的话即使样本统计值在小于190的小范围内仍然会通过经销商的原假设,换句话说对于生产厂商来说在小于190的小范围内的产品就损失了检验价值(即使这些产品是毫无疑问合格的),而经销商如果要得到温度小于190的备择假设,就需要统计值不仅要小于190,而且要尽量远离190,即发生显著性水平为0.05的事件,这对于产品要求来说是严格的.
符号检验
符号检验的应用场景:
- 检验的数据不是数值型
- 检验的数据是数值型,但不满足正态分布
符号检验的基本概念:
通过符号“+”和“-”的个数来进行统计推断的方法,称为符号检验。符号检验是最古老的检验方法之一。
说明:
符号检验本质上就是二项分布检验,因此,从二项分布的性质可知,
- 对于大样本数据,可用正态分布近似二项分布,可以使用正态近似计算(prop.test )函数
- 对于小样本数据,只能使用二项分布的精确计算(binom.test)函数
符号检验实例
例:某饮料店为了解顾客对饮料的爱好情况,进一步改进他们的工作,对顾客喜欢咖啡,还是喜欢奶茶,或者两者同样爱好进行了调查。该店在某日随机抽取13名顾客进行调查,顾客喜欢咖啡超过奶茶用“+”表示,喜欢奶茶超过咖啡用“-”表示,两者同样爱好用0表示。现将调查的结果列在下表,试分析顾客是喜欢咖啡,还是喜欢奶茶?
| 顾客 | 喜好 | 顾客 | 喜好 | 顾客 | 喜好 |
|---|---|---|---|---|---|
| 1 | + | 6 | 0 | 11 | + |
| 2 | - | 7 | + | 12 | - |
| 3 | + | 8 | - | 13 | + |
| 4 | + | 9 | + | ||
| 5 | + | 10 | + |
解:根据题意可检验如下假设
H0:顾客喜欢奶茶超过咖啡 (3)
H1:顾客喜欢咖啡超过奶茶 (9)
由于在调查数据中有1人(6号顾客)对咖啡和奶茶同样喜爱,用0表示,因而在样本容量中不加以计算,因此实际n=12.由于n值较小,所以选择精确二项分布检验,显著性水平取α=0.10
说明:出现负号的个数和出现正号的个数均服从二项分布B(12,1/2),负号个数越少,说明顾客喜欢咖啡超过奶茶的人数就越多,负号个数少到一定程度,就推翻H0,就接受H1,即顾客喜欢咖啡超过奶茶。原假设H0通常表示:不发生;备择假设H1alternative
hypothesis:备择假设把备择假设作为事件A,成功数为9

> binom.test(9,12,alternative = "great",conf.level = 0.90)
Exact binomial test
data: 9 and 12
number of successes = 9, number of trials = 12, p-value = 0.073
alternative hypothesis: true probability of success is greater than 0.5
90 percent confidence interval:
0.5247337 1.0000000
sample estimates:
probability of success
0.75
> binom.test(3,12,alternative = "less",conf.level = 0.90)
Exact binomial test
data: 3 and 12
number of successes = 3, number of trials = 12, p-value = 0.073
alternative hypothesis: true probability of success is less than 0.5
90 percent confidence interval:
0.0000000 0.4752663
sample estimates:
probability of success
0.25
结论:p-value=0.073<0.10,且区间估计为[0,0.475],因此拒绝原假设,接受备择假设,认为喜欢咖啡的人,超过喜欢奶茶的人。
符号秩检验与秩和检验
1、秩(Rank)的定义:
所谓秩,就是对样本的排序。设X1,X2,…, Xn为一组样本(不必取自同一总体),将X1,X2,…,Xn从小到大排成一列,用Ri记为Xi(i=1,2,3,…,n)在上述排列中的位置号,称R1,R2,…,Rn为样本X1,X2,…,Xn产生的秩统计量。
2、秩(Rank)的计算:
rank(x, na.last=TRUE, ties.method=c(“average”, ”first”,” random”, ”max”, ”min”))
- x:样本数据
- na.last:表示对NA值的处理方法
- ties.method:字符串,表示处理结的方法。
3、 Wilcoxon符号秩检验 (Wilcoxon signed-rank test)
Wilcoxon符号秩检验是用作单个总体X的中位数检验,即
- H0:M=M0 H1:M≠M0 (双侧检验)( M0 假设中位数,总体中位数)
- H0:M≥M0 H1:M<M0 (单侧检验)
- H0:M≤M0 H1:M>M0 (单侧检验)
设X1,X2,…,Xn是来自总体X的样本,假定X的分布是连续的,且关于中位数M0是对称的。将|Xi-M0|的差额,按照递增次序排列,并根据差额的次序给出相应的秩次Ri,。定义Xi-M0>0为正秩次,Xi-M0<0为负秩次,然后按照正秩次之和进行检验,即为秩次和检验。
说明:如果原观察值的数目为n’,减去Xi=M0的样本后,其样本数为n,用Ri(+)表示正秩次,W表示正秩次的和,则Wilcoxon统计量为:
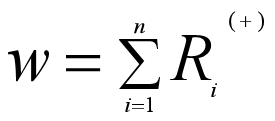
4、 Wilcoxon秩和检验 (Wilcoxon rank sum test)
Wilcoxon秩和检验是用作两个总体X和Y中位数差的检验,即
H0:M1-M2=M0,H1:M1-M2≠M0 (双侧检验)
H0:M1-M2 ≥ M0,H1:M1-M2<M0 (单侧检验)
H0:M1-M2 ≤ M0,H1:M1-M2>M0 (单侧检验)
假定X1,X2,…,Xn1是来自总体X的样本,Y1,Y2,…,Yn2是来自总体Y的样本。将样本的观察值排在一起, X1,X2,…,Xn1 , Y1,Y2,…,Yn2 ,仍设r1,r2,…rn1是样本X产生的秩统计量, R1,R2,…Rn2是样本Y产生的秩统计量,则wilcoxon-mann-whitney统计量定义为:
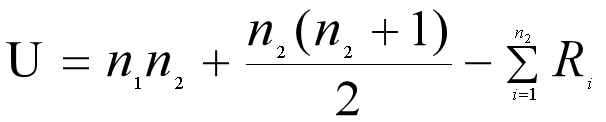
通过统计量U进行检验,称为Wilcoxon秩和检验。
Wilcoxon符号秩检验 (Wilcoxon signed-rank test)
在R语言中进行符号秩检验可以使用 wilcox.test( )
wilcox.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0, paired = FALSE, exact = NULL, correct = TRUE, conf.int = FALSE, conf.level = 0.95, ...)
- x,y是观察数据构成的数据向量。
- alternative是备择假设,有单侧检验和双侧检验,
- mu待检参数,如中位数M0.,或者中位数之差,默认为0.
- paired是逻辑变量,说明变量x,y是否为成对数据。
- exact是逻辑变量,说明是否精确计算P值,当样本量较小时,此参数起作用,当样本量较大时,软件采用正态分布近似计算P值。
- correct是逻辑变量,说明是否对P值的计算采用连续性修正,相同秩次较多时,统计量要校正。
- conf.int是逻辑变量,说明是否给出相应的置信区间。
例:假定某电池厂宣称该厂生产的某种型号电池寿命的中位数为140安培小时。为了检验该厂生产的电池是否符合其规定的标准,现从新近生产的一批电池中抽取了随机样本,并对这20个电池的寿命进行了测试,其结果如下(单位:安培小时):
137.0,140.0,138.3,139.0,144.3,139.1,141.7,137.3,133.5,138.2,141.1,139.2,136.5,136.5,135.6,138.0,140.9,140.6,136.3,134.1
试用Wilcoxon符号秩检验分析该厂生产的电池是否符合其标准。
(方法一,双侧检验)根据题意假设: H0:电池中位数M=140; H1:电池中位数≠140。
> wilcox.test(x,mu=140,exact=FALSE,correct=FALSE,conf.int=TRUE)
Wilcoxon signed rank test
data: x
V = 34, p-value = 0.01407
alternative hypothesis: true location is not equal to 140
95 percent confidence interval:
136.90 139.55
sample estimates:
(pseudo)median
138.2
结论: 这里V=34是wicoxon的统计量,P值<0.05,即拒绝原假设,接受备择假设,中位值小于140安培小时。
(方法二,单侧检验)根据题意假设: H0:电池中位数M>=140; H1:电池中位数<140。
> wilcox.test(x,mu=140,alternative="less",exact=FALSE,correct=FALSE,conf.int=TRUE)
Wilcoxon signed rank test
data: x
V = 34, p-value = 0.007034
alternative hypothesis: true location is less than 140
95 percent confidence interval:
-Inf 139.2
sample estimates:
(pseudo)median
138.2
结论: 这里V=34是wicoxon的统计量,P值<0.05,即拒绝原假设,接受备择假设,中位值小于140安培小时。
例:为了检验一种新的复合肥和原来使用的肥料相比是否显著提高了小麦的产量,在一个农场中选择了10块田地,每块等分为两部分,其中任指定一部分使用新的复合肥料,另一部分使用原肥料。小麦成熟后称得各部分小麦产量如下表所示。试用Wilcoxon符号检验法检验新复合肥是否会显著提高小麦的产量,并与符号检验作比较(α = 0.05)。
表:使用不同肥料情况下小麦的产量(单位:千克)
| 田块 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 新复合肥 | 459 | 367 | 303 | 392 | 310 | 342 | 421 | 446 | 430 | 412 |
| 原肥料 | 414 | 306 | 321 | 443 | 281 | 301 | 353 | 391 | 405 | 390 |
原假设是:两配对样本来自的两总体的分布无显著差异。
来自两个总体的样本进行检验,这是一组成对数据,要做成对数据的检验,即paired=TRUE
x<-c(495,367,303,392,310,342,421,446,430,412)
y<-c(414,306,321,443,281,301,353,391,405,390)
解:根据题意作如下假设:
H0:新复合肥的产量与原肥料的产量相同。(来自两总体的两配对样本无显著差异)
H1:新复合肥的产量高于原肥料的产量。
> x<-c(495,367,303,392,310,342,421,446,430,412)
> y<-c(414,306,321,443,281,301,353,391,405,390)
> wilcox.test(x,y,alternative = "greater",paired = TRUE)
Wilcoxon signed rank exact test
data: x and y
V = 48, p-value = 0.01855
alternative hypothesis: true location shift is greater than 0
结论:可见P值<0.05,拒绝原假设,即新复合肥能显著提高小麦产量。
真实位置偏移大于0
> wilcox.test(y,x,alternative ="less",paired=TRUE)
Wilcoxon signed rank exact test
data: y and x
V = 7, p-value = 0.01855
alternative hypothesis: true location shift is less than 0
> wilcox.test(y,x,alternative ="greater",paired=TRUE)
Wilcoxon signed rank exact test
data: y and x
V = 7, p-value = 0.9863
alternative hypothesis: true location shift is greater than 0
例:今测得7名非铅作业工人和7名铅作业工人的血铅值,如下表所示。试用Wilcoxon秩和检验分析两组工人血铅值有无差异。
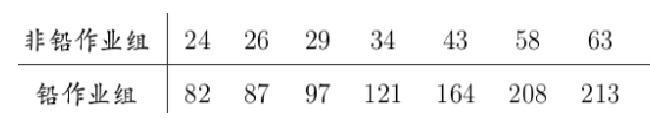
解:根据题意做如下假设
H0:两组工人血铅值无差异
H1:铅作业组血铅值高于非铅作业组
> wilcox.test(x,y,alternative = "less",paired = TRUE,correct = FALSE,exact = FALSE)
Wilcoxon signed rank test
data: x and y
V = 0, p-value = 0.008878
alternative hypothesis: true location shift is less than 0
例:某医院用某种药物治疗两种类型慢性支气管炎患者共216例,疗效如表所示,试分析该药物对两种类型慢性支气管炎的疗效是否相同。
表: 某种药物治疗两种类型慢性支气管炎疗效结果
| 疗效 | 控制 | 显著 | 进步 | 无效 |
|---|---|---|---|---|
| 单纯型 | 62 | 41 | 14 | 11 |
| 喘息型 | 20 | 37 | 16 | 15 |
Wilcoxon秩和检验
Wilcoxon秩和检验是用作两个总体X和Y中位数差的检验
解:每个病人的疗效用不同的值表示(1表示控制,2表示显著,3表示进步,4表示最差),这样可以对216名病人进行排序。
H0:M1-M2=0
H1:M1-M2≠0
> x<-rep(1:4,c(62,41,14,11))
> y<-rep(1:4,c(20,37,16,15))
> wilcox.test(x,y,conf.int=TRUE)
Wilcoxon rank sum test with continuity correction
data: x and y
W = 3994, p-value = 0.0001242
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
-9.999717e-01 -6.606939e-05
sample estimates:
difference in location
-0.9999808
因为数据有结点存在,故无法精确计算P值,其参数为exact=FALSE。
结论:
1)P值<0.05,因此拒绝原假设,即认为该药物对两种类型慢性支气管炎的治疗是不同的。
2)从置信区间来看,该药物治疗单纯型慢性支气管炎的效果好。
3)如果做单侧假设,H0:M1-M2>=0,H1: M1-M2<0,结论同上
总结:
- 是非参数统计中符号检验法的改进,它不仅利用了样本观察值与总体中位数之间的差的正负,还利用了差的值的大小信息。
- 虽然是简单的非参数方法,却体现了秩的基本信息。
- 用Wilcoxon符号秩检验方法可以检验一个样本是否来自某个总体。
- 用Wilcoxon符号秩检验方法可以用于成对样本的检验,从而说明两个总体是否存在显著差异。
独立性检验
独立性检验:是统计学的一种检验方式,皮尔森卡方检验(英文名:Pearson‘s chi square test),它是根据次数资料(频数信息)判断两类因子彼此相关或相互独立的假设检验。所谓独立性,就是指变量之间是独立的,没有关系。
所谓独立性检验就是检验:
H0:X与Y相互独立 (无关)
H1:X与Y不独立(相关)
本章介绍两种独立性检验方法:
- Pearson 卡方独立性检验——chisq.test()函数
- Fisher精确独立性检验——fisher.test()函数
Pearson(皮尔逊)卡方检验
概念:卡方检验是一种用途很广的计数资料的假设检验方法,由卡尔·皮尔逊提出。它属于非参数检验的范畴,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。
用途:通常卡方检验的应用主要为:
- 1、 卡方拟合优度检验
- 2、卡方独立性检验
非参数检验(Nonparametric tests)是统计分析方法的重要组成部分,它与参数检验共同构成统计推断的基本内容。非参数检验是在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。由于非参数检验方法在推断过程中不涉及有关总体分布的参数,因而得名为“非参数”检验。
卡方值:
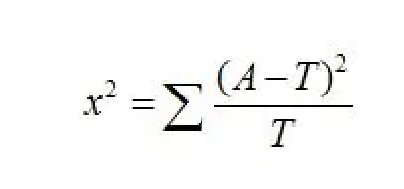
其中,A为实际值,T为理论值。
x2用于衡量实际值与理论值的差异程度(也就是卡方检验的核心思想),包含了以下两个信息:
- 实际值与理论值偏差的绝对大小(由于平方的存在,差异是被放大的)
- 差异程度与理论值的相对大小
例:为了研究吸烟是否与患肺癌有关,对63位肺癌患者及43位非肺癌患者调查了其中的吸烟人数,得到2*2列联表。试分析吸烟与患肺癌是否有关。
| 患肺癌 | 未患肺癌 | 合计 | |
|---|---|---|---|
| 吸烟 | 60 | 32 | 92 |
| 不吸烟 | 3 | 11 | 14 |
| 合计 | 63 | 43 | 106 |
H0:吸烟与肺癌无关
H1:吸烟与肺癌有关
> x<-matrix(c(60,3,32,11),nc=2)
> chisq.test(x)
Pearson's Chi-squared test with Yates' continuity correction
data: x
X-squared = 7.9327, df = 1, p-value = 0.004855
结论:P值(0.004855<0.05),拒绝原假设,即H0:X与Y独立,也就是说:吸烟与肺癌是有关的
例:在一次社会调查中,以问卷方式调查了总共901人的月收入及对工作的满意程度,其中收入A分为4档,对工作的满意程度B分为很不满意、较不满意、基本满意和很满意4档。调查结果用4*4列联表表示。分析工资收入与对工作的满意程度是否相关。
| 工资收入 | 很不满意 | 较不满意 | 基本满意 | 很满意 | 合计 |
|---|---|---|---|---|---|
| <3000 | 20 | 24 | 80 | 82 | 206 |
| 3000~7500 | 22 | 38 | 104 | 125 | 289 |
| 7500~12000 | 13 | 28 | 81 | 113 | 235 |
| >12000 | 7 | 18 | 54 | 92 | 171 |
| 合计 | 62 | 108 | 319 | 412 | 901 |
工资收入:将连续性变量类别化,分成四个区间
H0:满意成度与收入无关
H1:满意成度与收入有关
> x<-matrix(c(20,22,13,7,24,38,28,18,80,104,81,54,82,125,113,92),nc=4)
> chisq.test(x)
Pearson's Chi-squared test
data: x
X-squared = 11.989, df = 9, p-value = 0.214
结论:P值(0.214>0.05),接受原假设,即H0:X与Y独立,也就是说:对工作的满意程度与个人收入无关
例:对vcd包中的数据集Arthritis,试分析药物的治疗效果是否与性别相关。
> library(grid)
> library(vcd)
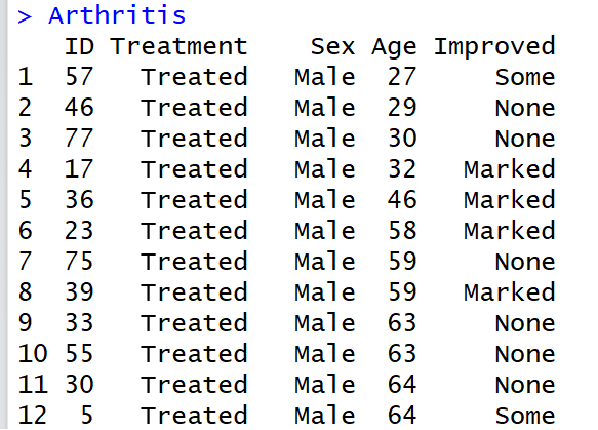
H0:药物的治疗效果与性别是独立的。
H1:药物的治疗效果与性别是相关的。
> mytable<-table(Arthritis$Sex,Arthritis$Improved)
> mytable
None Some Marked
Female 25 12 22
Male 17 2 6
> chisq.test(mytable)
Pearson's Chi-squared test
data: mytable
X-squared = 4.8407, df = 2, p-value = 0.08889
结论:P值(0.089>0.05),接受原假设,即H0:X与Y独立,也就是说: 药物的治疗效果与性别无关
Fisher精确独立性检验
费舍尔(Fisher)精确独立性检验在样本数较小时(单元的期望频数小于4),需要用Fisher精确检验来完成独立性检验。
例:某医师为研究乙肝免疫球蛋白预防胎儿宫内感染HBV的效果,将33例HBsAg阳性孕妇随机分为预防注射组和对照组。问两组新生儿的HBV总体感染率有无差别?
| 阳性 | 阴性 | 合计 | |
|---|---|---|---|
| 预防注射组 | 4 | 18 | 22 |
| 对照组 | 5 | 6 | 11 |
| 合计 | 9 | 24 | 33 |
> x<-matrix(c(4,5,18,6),nc=2)
> fisher.test(x)
Fisher's Exact Test for Count Data
data: x
p-value = 0.121
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.03974151 1.76726409
sample estimates:
odds ratio
0.2791061
结论:P值(=0.1.21)>0.05,并且优势比的置信区间包含1,接受原假设,即两变量是相互独立的,即认为两组新生儿的HBV总体感染率并无显著差异。
分布的检验
判断一组数据的分布是否来自于某一特定的分布。
Pearson拟合优度卡方检验
1、 理论分布完全已知的情况
2、 理论分布依赖于若干个未知参数的情况
在分布的检验中,适应性最广的检验是Pearson拟合优度检验
Pearson’s Chi-squared Test for Count Data
Description chisq.test performs chi-squared contingency table tests and goodness-of-fit tests.
chisq.test(x, y = NULL, correct = TRUE, p = rep(1/length(x), length(x)), rescale.p = FALSE,
simulate.p.value = FALSE, B = 2000)

例:大麦的杂交后代关于芒性的比例应是无芒:长芒:短芒=9:3:4.实际观测值为335:125:160.试检验观测值是否符合理论假设?
解:根据题意 H0: p1=9/16, p2=3/16, p3=4/16
> chisq.test(c(335,125,160),p=c(9,3,4)/16)
Chi-squared test for given probabilities
data: c(335, 125, 160)
X-squared = 1.362, df = 2, p-value = 0.5061
结论:p-value=0.5061>0.05,接受原假设,即大麦芒性的观测值与理论一致。
例:某消费者协会为了确定市场上消费者对5种品牌啤酒的喜好情况,随机抽取了1000名啤酒爱好者作为样本进行如下检验:每人得到5种品牌的啤酒各一瓶,但未标明牌子。这5种啤酒按分别写着A,B,C,D,E字母的5张纸片随机的顺序送给每一个人。下表是根据样本资料整理得到的各种品牌啤酒爱好者的频数分布。根据这些数据,判断消费者对这5种品牌啤酒的爱好有无明显差异。
5种品牌啤酒爱好者的频数
| 最喜欢的牌子 | A | B | C | D | E |
|---|---|---|---|---|---|
| 人数 | 210 | 312 | 170 | 85 | 223 |
解:如果消费者对5种品牌啤酒喜爱无显著差异,那么,就可以认为喜欢这5种品牌啤酒的人数呈均匀分布,即5种啤酒爱好者人数各占20%。因此,原假设:H0:喜好每种啤酒的人数呈均匀分布
> chisq.test(c(210,312,170,85,2233))#Chisq.test(X)只给出数据集,没有给出概率,说明采用默认值,等概率分布的
Chi-squared test for given probabilities
data: c(210, 312, 170, 85, 2233)
X-squared = 5567.8, df = 4, p-value < 2.2e-16
结论:p-value<<0.05,拒绝原假设,即认为消费者对于5种品牌啤酒的爱好是有显著差异的。
单样本泊松分布总体的均值检验(Poisson)
某一特定时间段或某空间段内事件发生的次数,该次数表示的变量为随机变量,服从泊松分布。例如:
- 30分钟内到达某修理厂的车辆数
- 50千米长的公路上需要修理汽车的数量
- 100千米长的管道上泄漏点的个数
- 一段时间内到某商店购物的顾客数
- 某超市中等待结账的顾客数
- 一段时间内经过某路口的汽车数
- 某地区一段时间内某年龄段的死亡人数
1 Poisson分布
如果事件满足以下两条性质:
(1)事件在任意两个等长度的区间内发生一次的概率相等;
(2)事件在任意区间内是否发生与其他地区的发生情况相互独立。
则:事件A发生的次数X就是一个可用Poisson分布来描述的随机变量。Poisson分布的分布率:
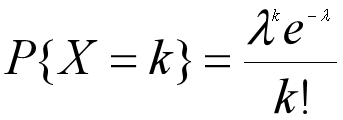
P{X=k}表示事件在一个区间内发生k次的概率,参数 λ \lambda λ表示在一个区间内事件发生次数的平均值或数学期望。
> x<-0:10
>y<-dpois(x,4)
[1] 0.0183 0.0733 0.1465 0.1954 0.1954 0.1563 0.1042 0.0595 0.0298 0.0132 0.0053
> plot(x, y, type="h", main="泊松分布图lambda=4")
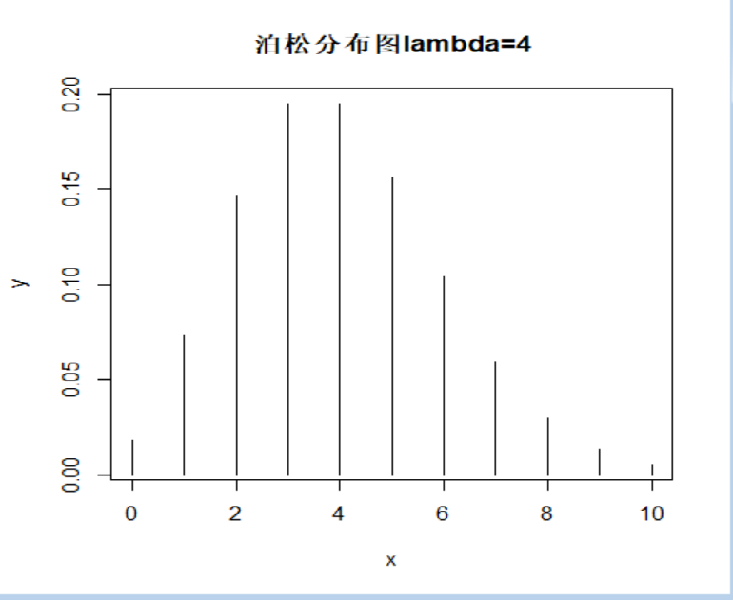
Description:
Density, distribution function, quantile function and random generation for the Poisson distribution with parameter lambda.
dpois(x,lambda,log=FALSE) 概率密度函数
ppois(q,lambda,lower.tail=TRUE,log.p=FALSE) 分布函数
qpois(p,lambda,lower.tail=TRUE,log.p=FALSE) 分位函数
rpois(n,lambda)
q: vector of quantiles.
p: vector of probabilities
假定顾客到达某银行的平均值是每4分钟3.2名,计算(1)在接下来的4分钟内,分别计算到达顾客数<6的概率;(2)在4分钟内至多有7名顾客到达的概率是多少?
解:(1)设X为4分钟内到达银行的顾客数,题意是计算P{X=0},P{X=1},…,P{X=5}.R程序及计算结果如下所示:
> x<-dpois(0:5,3.2)
> x
[1] 0.0407622 0.1304391 0.2087025 0.2226160 0.1780928 0.1139794
(2)设X为4分钟内到达银行的顾客数,题意是计算P{X≤7}.R程序及计算结果如下所示:
> ppois(7,3.2)
[1] 0.9831702
假定顾客到达某银行的平均值是每4分钟3.2名,计算(1)在4分钟内有7名以上顾客到达的概率;(2)在8分钟内到达10名的顾客的概率
解:(1)设X为4分钟内到达银行的顾客数,题意是计算P{X>7},即计算1-P{X≤7}.R程序及计算结果如下所示:
> 1-ppois(7,3.2)
[1] 0.01682984
结论:从这个结果来看,在4分钟内不大可能有7名以上顾客到达银行。
(2)首先调整参数lambda,其值由3.2调整为6.4,即8分钟内平均有6.4名顾客到达银行。 R程序及计算结果如下所示:
> dpois(10,lambda = 6.4)
[1] 0.05279004
在90%的概率下,4分钟内至多有几名顾客到达?
> qpois(0.90,3.2)
[1] 6
假设一次市场推广活动中前一个小时有50人注册,后一个小时有60人注册,问:后一小时的注册人数是否明显高于前一个小时?
H0:后一小时注册用户数量与前一小时无差异
H1:后一小时注册用户数量显著高于前一小时
> poisson.test(x=60,T=50,alternative="greater",conf.level=0.95)
Exact Poisson test
data: 60 time base: 50
number of events = 60, time base = 50, p-value = 0.09227
alternative hypothesis: true event rate is greater than 1
95 percent confidence interval:
0.9570464 Inf
sample estimates:
event rate
1.2
结论:P值(=0.09227)>0.05,,即接受原假设,说明后一小时的注册人数与前一小时无差异。
qpois()函数求在显著性水平和对比值下的泊松分布次数
> qpois(0.95,lambda=50)
[1] 62
> qpois(0.90,lambda=50)
[1] 59
> poisson.test(x=62,T=50,alternative="greater",conf.level=0.95)
Exact Poisson test
data: 62 time base: 50
number of events = 62, time base = 50, p-value = 0.05568
alternative hypothesis: true event rate is greater than 1
95 percent confidence interval:
0.9928263 Inf
sample estimates:
event rate
1.24
> poisson.test(x=63,T=50,alternative="greater",conf.level=0.95)
Exact Poisson test
data: 63 time base: 50
number of events = 63, time base = 50, p-value = 0.04239
alternative hypothesis: true event rate is greater than 1
95 percent confidence interval:
1.010742 Inf
sample estimates:
event rate
1.26
测试一组数据是否来自某一泊松分布
> data<-rpois(n=100,lambda=20)
> mean<-mean(data)
poisson.test (sum(data),T=length(data),mean)
Exact Poisson test
data: sum(data) time base: length(data)
number of events = 2109, time base = 100, p-value = 1
alternative hypothesis: true event rate is not equal to 21.09
95 percent confidence interval:
20.19942 22.00974
sample estimates:
event rate
21.09
结论:P=1,说明数据服从参数lambda=20的泊松分布。其中P值越大说明数据符合度越好
相关性检验
相关性检验correlation test是对变量之间是否相关以及相关的程度如何所进行的统计检验。相关系数可以用来描述定量变量之间的关系。相关系数的符号表明关系的方向(+ 正相关 - 负相关),其值的大小表示关系的强弱程度(完全不相关为0,完全相关时为1)。.
- Pearson(皮尔森)相关检验(针对正态分布数据)
- Spearman(斯皮尔曼)相关检验 (秩检验)
- Kendall(肯达尔)相关检验 (秩检验)
相关系数:最早由统计学家卡尔·皮尔逊设计的统计指标,是研究变量之间线性相关程度的量,一般用字母 r 表示。
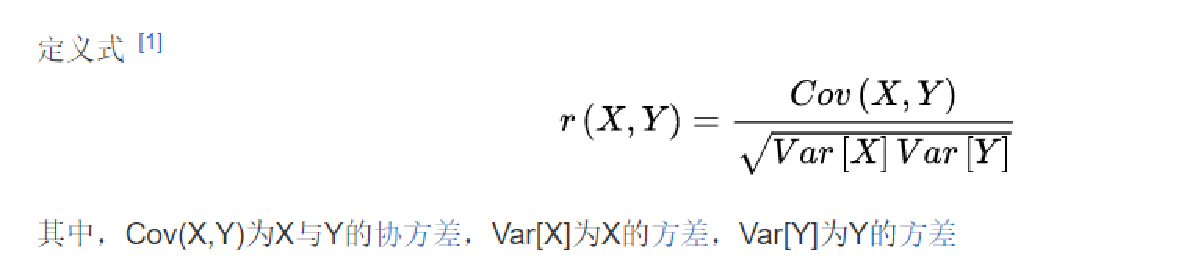
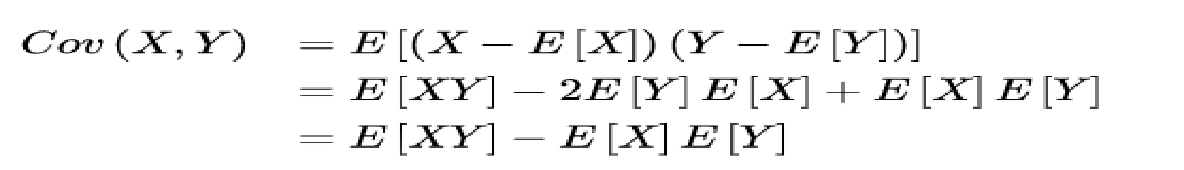
如果X与Y是统计独立的,那么二者之间的协方差就是0,因为两个独立的随机变量满足E[XY]=E[X]E[Y]。但是,反过来并不成立。即如果X与Y的协方差为0,二者并不一定是统计独立的。协方差为0的两个随机变量称为是不相关的。
函数的使用格式为:
cor.test(x, y, alternative = c(“two.sided”, “less”, “greater”), method = c("pearson", "kendall", "spearman"),conf.level = 0.95)
- 其中x,y是供检验的样本;
- alternative指定是双侧检验还是单侧检验,two-sided(默认值),相关,less表示单侧检验(负相关),greater表示单侧检验(正相关);
- method为检验的方法;
- conf.level为检验的置信水平。
Pearson(皮尔逊)相关检验
例:对于随机选取的20个黄麻个体植株,记录青植株重量Y与干植株重量X,设二元总体(X,Y)服从二维正态分布,试分析青植株重量与干植株重量是否有相关性。
| X | Y | X | Y | X | Y | |||
|---|---|---|---|---|---|---|---|---|
| 1 | 68 | 971 | 8 | 12 | 321 | 15 | 14 | 229 |
| 2 | 63 | 892 | 9 | 20 | 315 | 16 | 27 | 332 |
| 3 | 70 | 1125 | 10 | 30 | 375 | 17 | 17 | 185 |
| 4 | 6 | 82 | 11 | 33 | 462 | 18 | 53 | 703 |
| 5 | 65 | 931 | 12 | 27 | 352 | 19 | 62 | 872 |
| 6 | 9 | 112 | 13 | 21 | 305 | 20 | 65 | 740 |
| 7 | 10 | 162 | 14 | 5 | 84 |
原假设H0: ρ x y = 0 \rho_{xy}=0 ρxy=0 备择假设H1: ρ x y ≠ 0 \rho_{xy} \neq0 ρxy=0
> rt<-read.table("weight.data")
> with(rt,cor.test(X,Y))
Pearson's product-moment correlation
data: X and Y
t = 20.739, df = 18, p-value = 5.145e-14
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.9483279 0.9921092
sample estimates:
cor
0.9797091
默认是pearson相关性检验,由于这里假设数据服从二元正态分布,所以使用皮尔逊相关检验
结论:P值(=5.151✖10-14)<0.05,样本相关系数为0.9797,即拒绝原假设,说明两变量高度相关。
皮尔逊积矩相关系数(英语:Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs, 文章中常用r或Pearson’s r表示)用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。
Spearman秩相关检验

设(X1,Y1)、(X2,Y2)…(Xn,Yn)为取自某个二元总体的独立样本,要检验变量X与变量Y是否相关,通常设定原假设
H0:X与Y相互独立(不相关)
备择假设H1:X与Y相关
例:一项有六个人参加表演的竞赛,有两人进行评定,试检验这两个评定员对等级评定有无相关关系。
| 甲的打分 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 乙的打分 | 6 | 5 | 4 | 3 | 2 | 1 |
由于评定成绩是打分的等级,因而无法用Pearson相关检验。
> cor.test(1:6,6:1,method = "spearman")
Spearman's rank correlation rho
data: 1:6 and 6:1
S = 70, p-value = 0.002778
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-1
结论:P值(=0.002 778)<0.05,,即拒绝原假设,说明两变量X和Y相关。由于rho=-1,表示这两个量完全负相关,即两人的结论有关系,但是结论完全相反。
Kendall(肯德尔)相关检验
设定原假设
H0:X与Y相互独立(不相关)
3个备择假设H1:X与Y相关或者正相关或者负相关
例:某幼儿园对9对双胞胎的智力进行检验,并按照百分制打分,试采用Kendall相关检验方法检验双胞胎的智力是否相关。
| 先出生的儿童 | 86 | 77 | 68 | 91 | 70 | 71 | 85 | 87 | 63 |
|---|---|---|---|---|---|---|---|---|---|
| 后出生的儿童 | 88 | 76 | 64 | 96 | 65 | 80 | 81 | 72 | 60 |
由于数据不一定满足正态分布,因此使用Kendall秩相关检验方法
> X<-c(86,77,68,91,70,71,85,87,63)
> Y<-c(88,76,64,96,65,80,81,72,60)
> cor.test(X,Y,method = "kendall")
Kendall's rank correlation tau
data: X and Y
T = 31, p-value = 0.005886
alternative hypothesis: true tau is not equal to 0
sample estimates:
tau
0.7222222
结论:P值(=0.005 886)<0.05,,即拒绝原假设,说明双胞胎的智力是相关的。Kendall相关系数为0.72222,表明是正相关。
某种矿石中两种有用成分A,B,取10个样品,每个样品中成分A的含量百分数X(%),以及成分B的含量百分数y(%)数据如下表所示,对两组数据进行相关性检验。
| X(%) | 67 | 54 | 72 | 64 | 39 | 22 | 58 | 43 | 46 | 34 |
|---|---|---|---|---|---|---|---|---|---|---|
| Y(%) | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
> x=c(67, 54, 72, 64, 39, 22, 58, 43, 46, 34)
> y=c(24, 15, 23, 19, 16, 11, 20, 16, 17, 13)
> cor.test(x,y)
Pearson's product-moment correlation
data: x and y
t = 6.6518, df = 8, p-value = 0.0001605
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6910290 0.9813009
sample estimates:
cor
0.9202595
总结
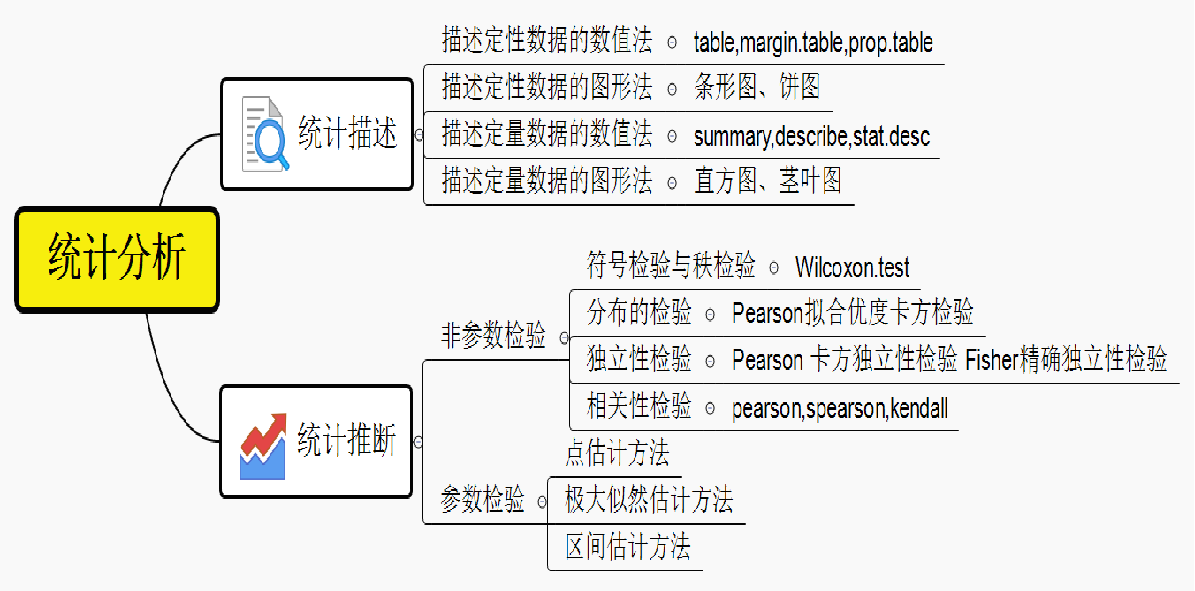
习题
- 使用sample函数模拟一次投掷一枚骰子的情况,共投掷100次,计算各点数出现的频数。
知识:简单随机抽样
sample(x,size,replace=FALSE,prob=NULL)
| 名称 | 取值与意义 |
|---|---|
| x | 向量,表示抽样的总体 |
| size | 非负整数,表示抽样的个体 |
| replace | 逻辑变量,表示是否为有放回抽样,默认为FALSE |
| prob | 数值向量(0-1之间),长度与参数x相同,表示x中元素出现的频率 |
> x<-sample(1:6,replace=TRUE,100)
> y<-table(x)
1 2 3 4 5 6
9 15 19 22 19 16
- 在某养鱼塘中,根据过去经验,鱼的长度的中位数为14.6cm,现对鱼塘中鱼的长度进行一次估测,随机地从鱼塘中取出10条鱼,长度数据保存在fish.data中,用Wilcoxon符号秩检验,试分析该鱼塘中鱼的长度是在中位数之上,还是在中位数之下?
表 鱼塘中捕捞出鱼的长度(单位:cm)
| 13.32 | 13.06 | 14.02 | 11.86 | 13.58 |
|---|---|---|---|---|
| 13.77 | 13.51 | 14.42 | 14.44 | 15.43 |
符号秩检验是基于中位数的检验
根据题意假设: H0:鱼塘中鱼的长度的中位数M>=14.6; H1:鱼塘中鱼的长度的中位数<14.6
> x<-unlist(as.vector(data))
> wilcox.test(x,mu=14.6,alternative="less",exact=FALSE,correct=FALSE,conf.int=TRUE)
Wilcoxon signed rank test
data: x
V = 4.5, p-value = 0.009491
alternative hypothesis: true location is less than 14.6
95 percent confidence interval:
-Inf 14.24504
sample estimates:
(pseudo)median
13.74995
结论: P值=0.009491<0.05,即拒绝原假设,接受备择假设,鱼塘中鱼的长度中位值小于14.6。
- Mendel用豌豆的两对相对性状进行杂交实验,黄色圆滑种子与绿色皱缩种子的豌豆杂交后,第二代根据自由组合规律,理论分离比为:实际实验值为:黄圆315 黄皱 101 绿圆 108 绿皱 32 ,共556粒。问此结果是否符合自由组合规律?
H0: 黄圆:黄皱:绿圆:绿皱=9/16:3/16:3/16:1/16
H1: 黄圆:黄皱:绿圆:绿皱≠9/16:3/16:3/16:1/16
应用卡方检验,判断一组数据的分布是否来自于某一特定的分布。
> chisq.test(c(315,101,108,32),p=c(9,3,3,1)/16)
Chi-squared test for given probabilities
data: c(315, 101, 108, 32)
X-squared = 0.47002, df = 3, p-value = 0.9254
结论: P值=0.9254>0.05,接受原假设,即该结果符合自由组合规律。
数学期望(Expectation):(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小,是对随机变量中心位置的度量。离散型随机变量的数学期望定义为:
结论:数学期望可以看成是随机变量取值的加权平均值,其权重就是概率。
方差(Deviation):用来度量随机变量和其数学期望(即均值)之间的平均偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
离散型方差的一般形式:已知离散型方差分布列:
X x1 x2 x3 … ** ** ** ** ** ** xn P p1 p2 p3 pn
- 某咨询机构每小时接到的咨询电话的电话数在0-5之间,相应的概率分布如表所示。计算咨询电话数的数学期望和方差。
接到电话的分布率
| 服务电话数 | 概率 | 服务电话数 | 概率 |
|---|---|---|---|
| 0 | 0.10 | 3 | 0.20 |
| 1 | 0.15 | 4 | 0.15 |
| 2 | 0.30 | 5 | 0.10 |
> x<-0:5
> x
[1] 0 1 2 3 4 5
> y<-c(0.1,0.15,0.3,0.2,0.15,0.1)
> E<-sum(x*y)
> E
[1] 2.45
> D<-sum(x^2*y)-E^2
> D
[1] 2.0475
> x<-0:5
> y<-c(0.1,0.15,0.3,0.2,0.15,0.1)
> sum((x-mean(x))^2*y)
[1] 2.05
方差=平方的数学期望-数学期望的平方
- 某饭店经理希望用统计的方法预测顾客数,他首先收集数据,指定一名服务员连续三周统计每周六晚7时至8时每5分钟内到达饭店的顾客数,如表所示,经理用连续三周的数据作为统计分析参数lambda的基础。如果顾客到达饭店的人数服从Poisson分布,用经理得到的lambda值预测周六晚7时-8时的下列问题:
(1)此时lambda的值是多少?
> x<-c(3,1,5,6,2,3,4,4,5,6,0,3,2,2,5,3,6,4,1,5,7,5,4,3,1,2,4,0,5,8,3,3,1,3,4,3)
> lambda<-mean(x)
> lambda
[1] 3.5
(2)5分钟内没有顾客到达的概率
> dpois(0,3.5)
[1] 0.03019738
(3)5分钟内有6名以上(包含6名)顾客到达的概率
> 1-ppois(5,3.5)
[1] 0.1423864
(4)10分钟内有4名以下(含4名)顾客到达的概率
> ppois(4,7)
[1] 0.1729916
(5)10分钟内有3-6名(包含3和6)顾客到达的概率
> sum(dpois(3:6,lambda*2))
[1] 0.4200749
> ppois(6,7)-ppois(2,7)
[1] 0.4200749
(6)15分钟内恰好有8名顾客到达的概率
> dpois(8,lambda=3.5*3)
[1] 0.1009025
- 调查某大学学生每周学习时间与得分的平均等级之间的关系,现抽查10个学生的资料如student.data文件所示。其中等级10表示最好,1表示最差,试用秩相关检验(Spearman检验和Kendall检验)分析学习时间和学习等级有无关系。(相关性检验)
解:设H0:X与Y相互独立(不相关),H1:X与Y相关
> x<-read.table("E:\\fyh\\sjy\\R\\student.data")
时间 等级
1 24 8
2 17 1
3 20 4
4 41 7
5 52 9
6 23 5
7 46 1
8 18 3
9 15 2
10 29 6
> time<-x[,1]
> level<-x[,2]
> time
[1] 24 17 20 41 52 23 46 18 15 29
> level
[1] 8 1 4 7 9 5 1 3 2 6
> cor.test(time,level,method="spearman")
Spearman's rank correlation rho
data: time and level
S = 72.72, p-value = 0.09279
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.5592731
> cor.test(time,level,method="kendall")
Kendall's rank correlation tau
data: time and level
z = 2.1553, p-value = 0.03114
alternative hypothesis: true tau is not equal to 0
sample estimates:
tau
0.5393599
说明:Kendall检验和Spearman检验的区别在于,Kendall是单调相关性,某一列需要比较的数据要有序。
- 文件score.data中的数据列出某高中18名学生某门课程的高考成绩和模拟考试成绩,这组数据能否说明高考成绩与模拟考试成绩是相关的?(相关性检验)
解:
H0:高考成绩X与模拟成绩Y相互独立(不相关)
H1:高考成绩X与模拟成绩Y相关
> data<-read.table('D:/R语言/作业/score.data')
> data
高考 模拟
1 87 90
2 76 98
3 77 92
4 85 87
5 89 87
6 83 62
7 78 65
8 91 90
9 76 84
10 100 92
11 96 100
12 96 98
13 90 100
14 92 97
15 100 97
16 100 95
17 90 94
18 99 100
> x<-data[,1]
> x
[1] 87 76 77 85 89 83 78 91 76 100 96 96 90 92 100 100 90 99
> y<-data[,2]
> y
[1] 90 98 92 87 87 62 65 90 84 92 100 98 100 97 97 95 94 100
> cor.test(x,y)
Pearson's product-moment correlation
data: x and y
t = 2.4133, df = 16, p-value = 0.02817
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.06551085 0.79235424
sample estimates:
cor
0.5165813
结论:p-value=0.02817<0.05,拒绝原假设,接受备择假设,即高考成绩与模拟成绩相关,相关系数0.5165.
- 一所大学去年收到21位男生和63位女生的求职信,结果聘用了10位男生和14位女生(1)分析这所大学在招聘方面是否存在性别差异;(2)根据学院详细分类数据如表所示,再研究该大学在招聘方面是否存在性别差异。
| 申请者 | 教育学院 | 管理学院 | 工程学院 | |||
|---|---|---|---|---|---|---|
| 聘 | 拒 | 聘 | 拒 | 聘 | 拒 | |
| 男性 | 2 | 8 | 5 | 0 | 3 | 3 |
| 女性 | 12 | 48 | 1 | 0 | 1 | 1 |
(1)原假设H0:招聘过程中的被聘被拒与性别无关 (不存在性别差异)
备择假设H1:招聘过程中的被聘被拒与性别有关(存在性别差异)
> data<-matrix(c(10,14,11,49),nc=2)
> chisq.test(data)
Pearson's Chi-squared test with Yates' continuity correction
data: data
X-squared = 3.8111, df = 1, p-value = 0.05091
> data2<-matrix(c(2,12,5,1,3,1,8,48,0,0,3,1),nc=2)
> chisq.test(data2)
Pearson's Chi-squared test
data: data2
X-squared = 19.32, df = 5, p-value = 0.001675
Warning message:
In chisq.test(data2) : Chi-squared近似算法有可能不准
- 某制造企业正在尝试确定两种方法在任务完成时间上存在的差异,他们随机选取11名工人,每名工人均用两种方法完成任务,其结果如图所示,(数据保存在task.data中),试用这组数据分析,两种方法在任务完成时间上是否存在显著差异?
本例可以采用Wilcoxon秩和检验作两个总体X与Y中位数差的检验,因此做检验
H0:M1-M2=0
H1:M1-M2≠0
本例是一组成对数据,因此要做成对数据的检验,因此,paired=TRUE
> v1<-data[,1]
> v1
[1] 10.2 9.6 9.2 10.6 9.9 10.2 10.6 10.0 11.2 10.7 10.6
> v2<-data[,2]
> v2
[1] 9.5 9.8 8.8 10.1 10.3 9.3 10.5 10.0 10.6 10.2 9.8
> wilcox.test(v1,v2,paired = TRUE,exact = FALSE,conf.int = TRUE)
Wilcoxon signed rank test with continuity correction
data: v1 and v2
V = 49, p-value = 0.0322
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
0.05000324 0.70003341
sample estimates:
(pseudo)median
0.4499906
P=0.0322<0.05,拒绝原假设,备择假设成立,即两组数据存在显著差异
- 用两种不同的方法测定同一种中草药的有效成分,共重复20次,得到实验结果如下所示
(1)试用符号检验法检验两测定有无显著差异
(2)试用Wilcoxon符号秩检验法检验两测定有无显著差异
(3)试用Wilcoxon秩和检验法检验两测定有无显著差异。
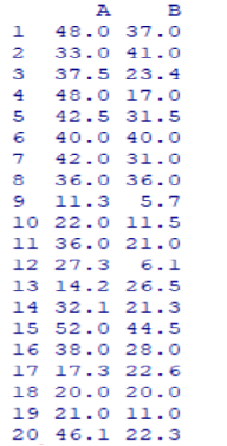
(1) 符号检验法:设方法A测得的有效成分高于方法B用正号表示,否则用负号表示
> y<-x[,1]-x[,2]
> y
[1] 11.0 -8.0 14.1 31.0 11.0 0.0 11.0 0.0 5.6 10.5 15.0 21.2 -12.3 10.8 7.5 10.0 -5.3 0.0 10.0 23.8
> cnt<-table(y<0)
> cnt
FALSE TRUE
17 3
H0:方法A测得的有效成分低于方法B测得的有效成分
H1:方法A测得的有效成分高于方法B测得的有效成分
> binom.test(17,20,al="greater",conf.level=0.95)
Exact binomial test
data: 17 and 20
number of successes = 17, number of trials = 20, p-value = 0.001288
alternative hypothesis: true probability of success is greater than 0.5
95 percent confidence interval:
0.6563362 1.0000000
sample estimates:
probability of success
0.85
本例可以采用Wilcoxon秩和检验作两个总体X与Y中位数差的检验,因此做检验
H0:M1-M2=0
H1:M1-M2≠0
本例是一组成对数据,因此要做成对数据的检验,因此,paired=TRUE
> wilcox.test(x[,1],x[,2],paired=TRUE,exact=F,conf.int=T)
Wilcoxon signed rank test with continuity correction
data: x[, 1] and x[, 2]
V = 136, p-value = 0.005191
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
2.850012 15.600045
sample estimates:
(pseudo)median
10.50005
- 为了了解新的数学教学方法的效果是否比原来方法的效果有所提高,从水平相当的10名学生中随机地各选5名接受新方法和原方法进行教学试验。充分长一段时间后,由专家通过各种方式对10名学生的数学能力予以综合评估(为公正起见,假定专家对各个学生属于哪一组并不知道),并按照数学能力由弱到强排序,结果如表所示,对alpha=0.05,检验新方法是否比原方法显著提高教学效果?
学生数学能力排序结果
| 新方法 | 3 | 5 | 7 | 9 | 10 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 原方法 | 1 | 2 | 4 | 6 | 8 |
说明:Wilcoxon秩和检验本质就需要排出样本的秩次,题目中的数据本身就是一个排序,因此,可直接试用Wilcoxon秩和检验。根据题意,需要检验:
H0:M1-M2≤0 H1:M1-M2>0
通过反证法的思想,希望证明的结论与备择假设相同
来自两个样本,通过中位数差进行秩和检验。
> x<-c(3,5,7,9,10)
> y<-c(1,2,4,6,8)
> wilcox.test(x,y,alternative="greater")
Wilcoxon rank sum exact test
data: x and y
W = 19, p-value = 0.1111
alternative hypothesis: true location shift is greater than 0
结论:p-value>0.05,无法拒绝原假设,即M1≤M2,并不能认为新的教学效果显著优于原方法。
cnt<-table(y<0)
cnt
FALSE TRUE
17 3
H0:方法A测得的有效成分低于方法B测得的有效成分
H1:方法A测得的有效成分高于方法B测得的有效成分
```R
> binom.test(17,20,al="greater",conf.level=0.95)
Exact binomial test
data: 17 and 20
number of successes = 17, number of trials = 20, p-value = 0.001288
alternative hypothesis: true probability of success is greater than 0.5
95 percent confidence interval:
0.6563362 1.0000000
sample estimates:
probability of success
0.85
本例可以采用Wilcoxon秩和检验作两个总体X与Y中位数差的检验,因此做检验
H0:M1-M2=0
H1:M1-M2≠0
本例是一组成对数据,因此要做成对数据的检验,因此,paired=TRUE
> wilcox.test(x[,1],x[,2],paired=TRUE,exact=F,conf.int=T)
Wilcoxon signed rank test with continuity correction
data: x[, 1] and x[, 2]
V = 136, p-value = 0.005191
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
2.850012 15.600045
sample estimates:
(pseudo)median
10.50005
- 为了了解新的数学教学方法的效果是否比原来方法的效果有所提高,从水平相当的10名学生中随机地各选5名接受新方法和原方法进行教学试验。充分长一段时间后,由专家通过各种方式对10名学生的数学能力予以综合评估(为公正起见,假定专家对各个学生属于哪一组并不知道),并按照数学能力由弱到强排序,结果如表所示,对alpha=0.05,检验新方法是否比原方法显著提高教学效果?
学生数学能力排序结果
| 新方法 | 3 | 5 | 7 | 9 | 10 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 原方法 | 1 | 2 | 4 | 6 | 8 |
说明:Wilcoxon秩和检验本质就需要排出样本的秩次,题目中的数据本身就是一个排序,因此,可直接试用Wilcoxon秩和检验。根据题意,需要检验:
H0:M1-M2≤0 H1:M1-M2>0
通过反证法的思想,希望证明的结论与备择假设相同
来自两个样本,通过中位数差进行秩和检验。
> x<-c(3,5,7,9,10)
> y<-c(1,2,4,6,8)
> wilcox.test(x,y,alternative="greater")
Wilcoxon rank sum exact test
data: x and y
W = 19, p-value = 0.1111
alternative hypothesis: true location shift is greater than 0
结论:p-value>0.05,无法拒绝原假设,即M1≤M2,并不能认为新的教学效果显著优于原方法。