原文:https://mp.weixin.qq.com/s/vPNPdbZy11q1qsfEz9etZQ
1 熵权法简介
熵源自于希腊语 “ 变化 ” 表示变化的容量,德国物理学家克劳修斯为了将热力学第二定律格式化而引入熵的概念 。
熵的概念来源于热力学,是用来描述过程的不可逆现象 。后来申农最先将熵引入信息论,在信息论中用熵来表示事物出现的不确定性,将熵作为不确定性的度量 。
熵权法是一 种根据各项指标调研数据所提供的信息量大小来确定指标权重的方法,其基本原理为若某个指标的熵值较小 、熵权较大时说明该指标能够提供的信息量越多,在决策时能起到的作用也越大;相反,某个指标的熵值较大、熵权较小时说明该指标能够提供的信息量越少,在决策时起到的作用也就越小。
熵权法是一种依赖于数据本身离散性的客观赋值法,用于结合多种指标对样本进行综合打分,实现样本间比较。
2 熵权法计算步骤
1)选取数据
选取
m
m
m 个指标,共
n
n
n 个样本,则
X
i
j
X_{ij}
Xij 为第
i
i
i 个样本的第
j
j
j 个指标的数值:
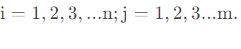
2)数据标准化处理
各项指标的计量单位以及方向不统一的情况下,需要对对数据进行标准化,为了避免求熵值时对数无意义,可以为每个0值加上较小数量级的实数,如0.01。
- 对于正向指标(越大越好的指标)

- 对于负向指标(越小越好的指标)
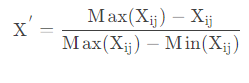
3) 计算第 j j j 项指标下第 i i i 个样本占该指标的比重
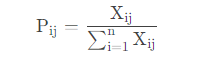
4)计算第 j j j 项指标的熵值
熵越大说明系统越混乱,携带的信息越少,熵越小系统越有序,携带的信息越多。
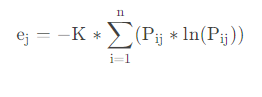
P i j = 0 P_{ij}=0 Pij=0 时, e j = 0 e_j=0 ej=0; K = 1 ln ( n ) K=\frac{1}{\ln (n)} K=ln(n)1,其中 n n n 为样本个数。
5)计算第 j j j 项指标的差异系数
某项指标的信息效用值取决于该指标的信息熵 e j e_j ej 与 1 之间的差值,它的值直接影响权重的大小。信息效用值越大,对评价的重要性就越大,权重也就越大。
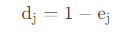
6)计算评价指标权重
利用熵值法估算各指标的权重,其本质是利用该指标信息的差异系数来计算,其差异系数越高,对评价的重要性就越大(或称权重越大,对评价结果的贡献就越大)
第 j j j项指标的权重:
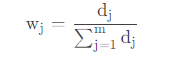
7)计算各样本综合得分
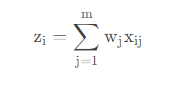
3 python实现
import numpy as np
#输入数据
loss = np.random.uniform(1, 4, size=5)
active_number = np.array([2, 4, 5, 3, 2])
data = np.array([loss, active_number]) # 2个变量5个样本
print(data)
# 定义熵值法函数
def cal_weight(x):
'''熵值法计算变量的权重'''
# 正向化指标
#x = (x - np.max(x, axis=1).reshape((2, 1))) / (np.max(x, axis=1).reshape((2, 1)) - np.min(x, axis=1).reshape((2, 1)))
# 反向化指标
x = (np.max(x, axis=1).reshape((2, 1)) - x) / (np.max(x, axis=1).reshape((2, 1)) - np.min(x, axis=1).reshape((2, 1)))
#计算第i个研究对象某项指标的比重
Pij = x / np.sum(x, axis=1).reshape((2, 1))
ajs = []
#某项指标的熵值e
for i in Pij:
for j in i:
if j != 0:
a = j * np.log(j)
ajs.append(a)
else:
a = 0
ajs.append(a)
ajs = np.array(ajs).reshape((2, 5))
e = -(1 / np.log(5)) * np.sum(ajs, axis=1)
#计算差异系数
g = 1 - e
#给指标赋权,定义权重
w = g / np.sum(g, axis=0)
return w
w = cal_weight(data)
print(w)
结果:
[[1.57242561 1.12780429 2.24411338 2.36236155 2.37789035]
[2. 4. 5. 3. 2. ]]
[0.70534397 0.29465603]
参考:
https://blog.csdn.net/weixin_43425784/article/details/107047869
https://blog.csdn.net/mzy20010420/article/details/127327787



![[附源码]Python计算机毕业设计高校教室申请管理系统](https://img-blog.csdnimg.cn/3f30ddf1da7242269b1a175b4d47cfd7.png)
![[附源码]Python计算机毕业设计电影网站系统设计](https://img-blog.csdnimg.cn/e1bfa4d0cd7342b8836acbf189ac5c4f.png)