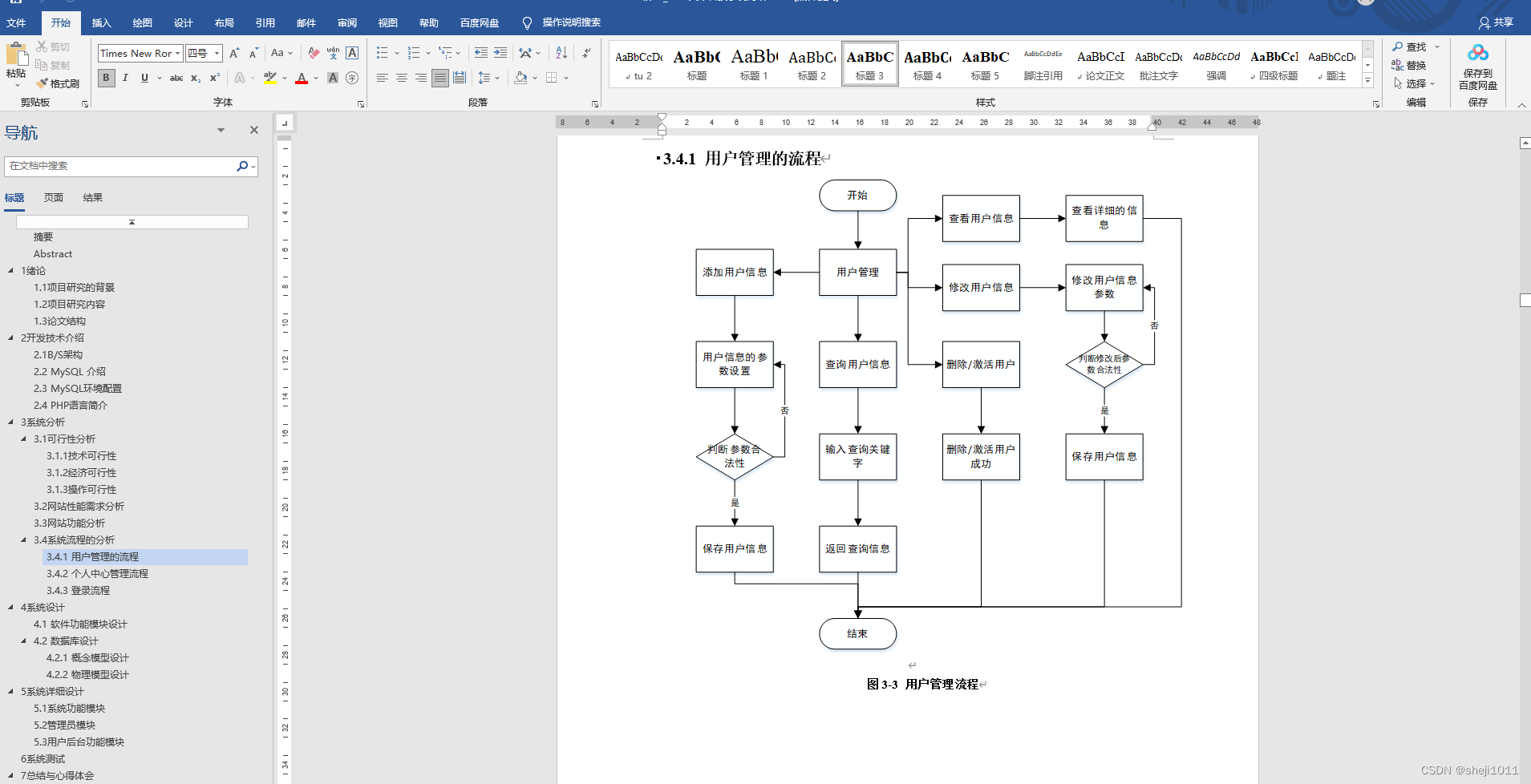
- 来自阿里
- MNN有三个贡献点:
- 提出了预推理机制,在线计算推理成本和最优方案
- 优化了kernel
- 提出后端抽象实现混合调度
- MNN的架构:

- 分离线和在线两部分。
- 离线就是很传统的模型转换、优化、压缩、量化的那一套东西,这里mnn转出的模型文件,后缀是.mnn的。
- 设备上的在线推理有三个部分:
- 预推理、kernel优化和后端抽象。每个算子在预推理的时候,结合算子信息和后端信息,做成本评估,从方案池里面找一个最优方案出来。然后再对方案做kernel级别的优化,整点SIMD啥的。后端抽象了之后就可以支持各种各样的后端。
- 预推理是假设输入大小是固定的,那么计算过程中的内存大小和计算成本都可以预先确定,实现加速。分两个部分:
- 计算方案选择、准备-执行的解耦。
- 计算方案选择:成本评估机制:C(total)=C(算法)+C(后端) ,C表示成本。
- C(算法):以卷积为例,有滑窗和Winograd两种实现可选,总体思路是根据不同的卷积动态选最小化计算成本的方法:
- 如果k=1,那就是个矩阵乘法而已,直接用Strassen算法
- 如果k>1就用Winograd将卷积转换成矩阵乘法。
- 如果输出大小是1,那就要用滑窗,不然就继续用Winograd了
- C(后端):把不同后端的所有算子时间都加起来,然后选时间成本最小的,后端算子的成本计算:

- MUL就是乘法次数,FLOPS 和 t_schedule都是后端的确定常量。
- C(算法):以卷积为例,有滑窗和Winograd两种实现可选,总体思路是根据不同的卷积动态选最小化计算成本的方法:
- 准备-执行的解耦:
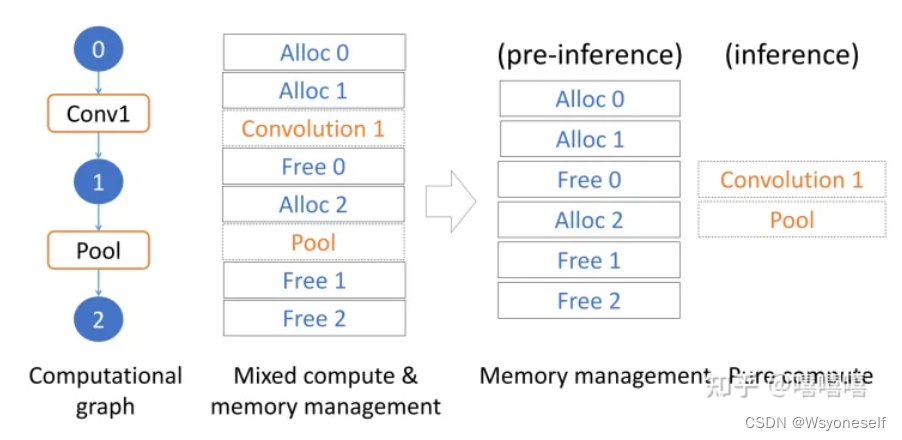 这个就比较暴力,就是预推理的时候,把网络跑一边,确定下来内存池,真正推理的时候就重用这个内存池,省去频繁的开辟和释放内存。
这个就比较暴力,就是预推理的时候,把网络跑一边,确定下来内存池,真正推理的时候就重用这个内存池,省去频繁的开辟和释放内存。
- kernel优化包含两部分,算法优化和调度优化,目标是用复杂度最低的算法,做最高效的调度。作者们主要做了两个:
- 一个是Winograd的优化
- 另一个是大矩阵乘的优化:就是前面说的那个Strassen算法加速矩阵运算,MNN是第一个用上这个来加速的推理引擎。Strassen是用加法替换乘法,需要递归调用来最大小性能。在MNN中,对于一个矩阵乘[n,k] X [k,m] ->[n,m] ,直接的乘法次数是mnk ,用Strassen的话只要7*m/2*n/2*k/2 次,但还额外要4次大小为[m/2,k/2] 的矩阵加、4次大小为[n/2,k/2] 的矩阵加、7次大小为 [m/2,n/2]的矩阵加法。所以Strassen算法递归执行的条件是:
mnk- 7*m/2*n/2*k/2 >4*m/2*k/2+4*n/2*k/2+7*m/2*n/2
- 后端抽象类的优点:
- 降低复杂度:这个Backend类统一管理资源加载和内存分配,做前端的可以专心搞算子,做后端的可以专心搞后端API
- 混合调度:MNN可以灵活组合不同后端的算子混合执行,例如卷积在CPU上跑,ReLU又能放到GPU上跑,就是玩
- 轻便:前后端结构,后端可抽离,例如Android不支持Metal就可以直接把Metal模块移除掉,MNN号称支持最全后端
- MNN没有局限于逐个算子优化,而是优化了算子更底层的依赖,例如矩阵乘,可以让新算子得到更简单的加速和优化。
MNN--初步学习
news2026/2/10 22:00:32
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/39386.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【外卖项目实战开发三】
文章目录分类管理业务开发公共字段自动填充问题分析代码实现功能完善新增分类需求分析数据模型代码开发分类信息分页查询需求分析代码开发删除分类需求分析代码开发代码完善关键代码修改分类需求分析代码实现分类管理业务开发
公共字段自动填充
问题分析
前面我们已经完成了…
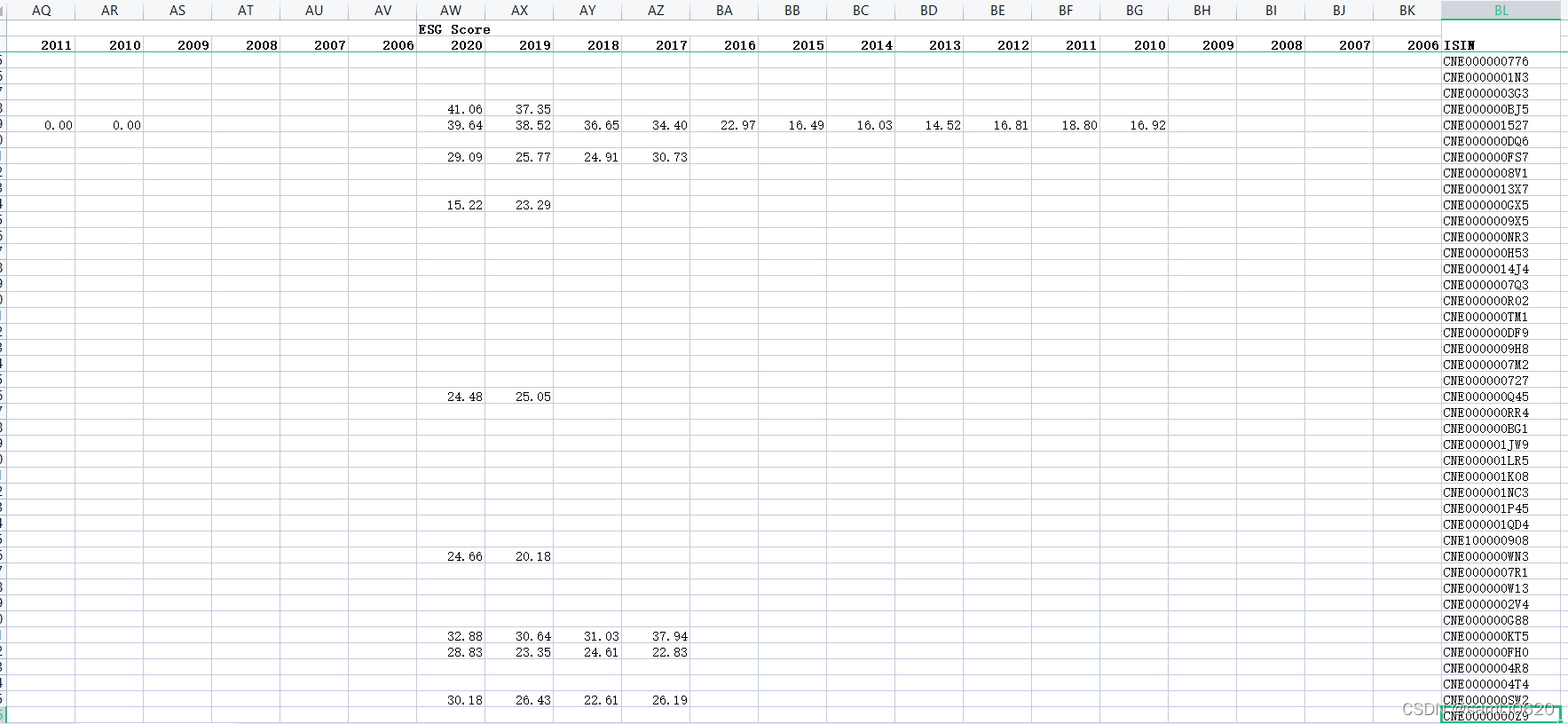
A股上市公司MSCI指数和ESG评级效果(2010-2021年)
1、数据来源:摩根斯坦利资本国际公司(Morgan Stanley Capital International)
2、时间跨度:2010--2021
3、区域范围:A股上市公司
4、指标说明:
ESG是英文Environmental(环境)、Social(社会&…
《人月神话》(The Mythical Man-Month)6贯彻执行(Passing the Word)
《人月神话》(The Mythical Man-Month)Chapter 6. 贯彻执行 Passing the Word他只是坐在那里,嘴里说:"做这个!做那个!"当然,什么都不会发生,光说不做是没有用的。- 哈里杜…
基于主从博弈的社区综合能源系统分布式协同优化运行策略matlab/cplex程序
基于主从博弈的社区综合能源系统分布式协同优化运行策略matlab/cplex程序 随着能源市场由传统的垂直一体式结构向交互竞争型 结构转变,社区综合能源系统的分布式特征愈发明显,传统 的集中优化方法难以揭示多主体间的交互行为。该文提出一 种基于主从博弈…
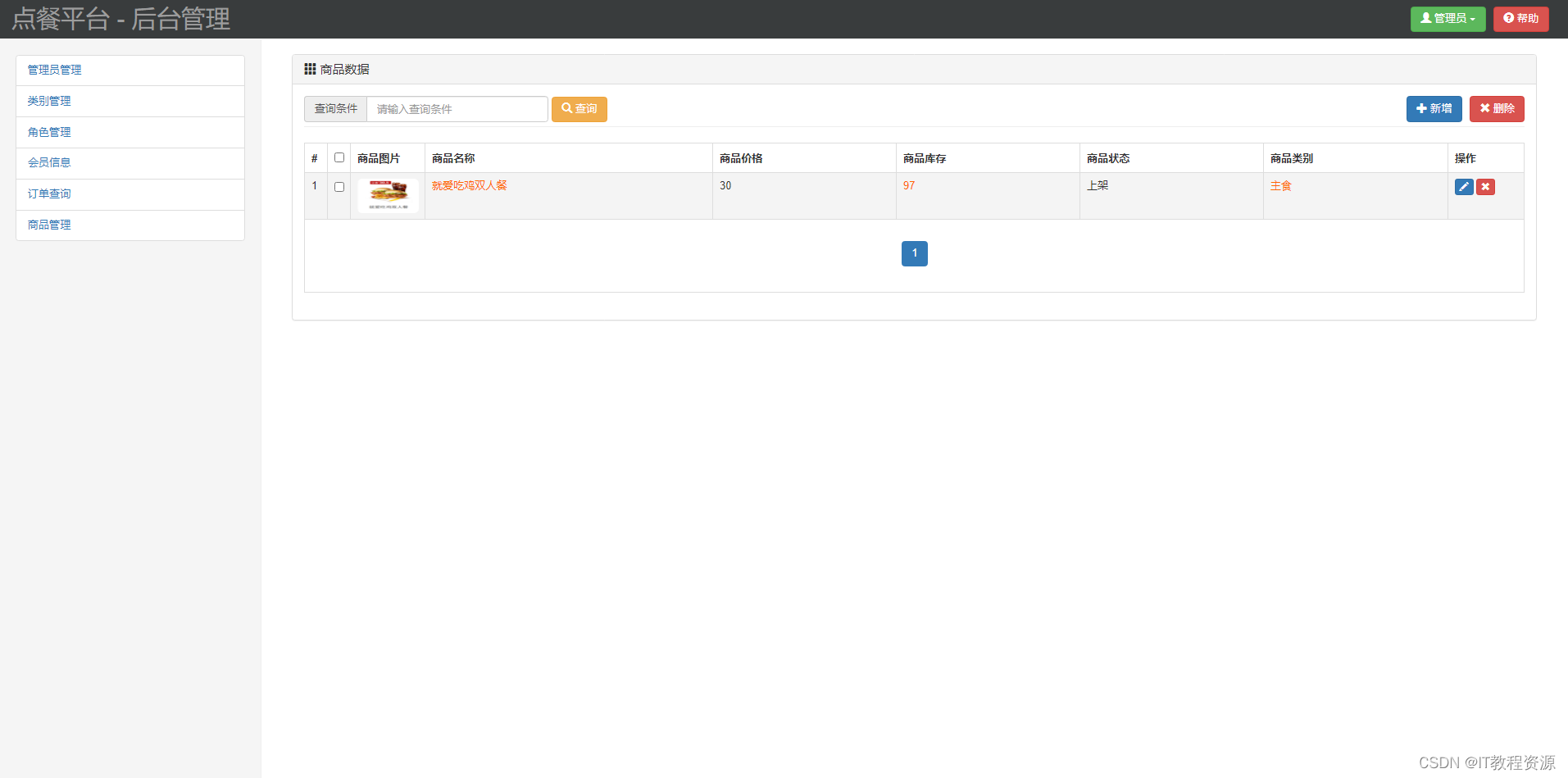
(免费分享)基于ssm在线点餐
源码获取:关注文末gongzhonghao,017领取下载链接
开发工具:IDEA ,Tomcat8.0,数据库:mysql5.7 /*** FileName: CategoryController** Date: 2020/9/30 17:04* Description:*/
package com.qst.goldenarches.contro…
关于环境保护html网页设计完整版-4环保垃圾分类5页
⛵ 源码获取 文末联系 ✈ Web前端开发技术 描述 网页设计题材,DIVCSS 布局制作,HTMLCSS网页设计期末课程大作业 | 环境保护 | 保护地球 | 校园环保 | 垃圾分类 | 绿色家园 | 等网站的设计与制作HTML期末大学生网页设计作业 HTML:结构 CSS:样…
Node.js 入门教程 14 使用 exports 从 Node.js 文件中公开功能
Node.js 入门教程 Node.js官方入门教程 Node.js中文网 本文仅用于学习记录,不存在任何商业用途,如侵删 文章目录Node.js 入门教程14 使用 exports 从 Node.js 文件中公开功能14 使用 exports 从 Node.js 文件中公开功能
Node.js 具有内置的模块系统。
…
Python脚本实现BJTU校园网自动登录
文章目录 1.背景介绍2.登录分析3.代码分析4.源代码1.背景介绍
BJTU的校园网连接好以后需要输入账号和密码才能正确登录,如下图所示。整个流程比较繁琐,尤其是很多服务器、工作站是无图形化的系统,大部分时间需要SSH连接,所以通过界面登录十分不方便。 所以就想了一个办法,…
(附源码)计算机毕业设计Java办公自动化管理系统
项目运行
环境配置:
Jdk1.8 Tomcat8.5 Mysql HBuilderX(Webstorm也行) Eclispe(IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持)。
项目技术:
Springboot mybatis Maven Vue 等等组成,B/…
(附源码)计算机毕业设计Java巴州监控中心人事管理系统
项目运行
环境配置:
Jdk1.8 Tomcat8.5 Mysql HBuilderX(Webstorm也行) Eclispe(IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持)。
项目技术:
Springboot mybatis Maven Vue 等等组成,B/…
java_ 多线程知识笔记(一)
文章目录前言:1.如何理解线程2.进程和线程的关系3.多线程编程第一种:继承Thread类第二种:实现Runnable 接口:第三种:使用Lambda表达式4.Thread 用法1.Thread常见的构造方法2.Thread的几个常见的属性5.等待一个线程6.并发和并行前言:
为什么要引入多线程编程 java引用进程的概…
【好书推荐】计算机网络:自顶向下方法(第七版)
人生的美妙之处在于迷上一样东西。人生苦短,少做些虚无缥缈的事。 – 刘慈欣-《三体》 推荐理由
自计算机网络诞生以来,经过数十年的发展,计算机的体系已经非常庞大,同时计算机网络也大大促进了人类社会的发展。无数大佬前赴后继…
【python量化】将Informer用于股价预测
写在前面Informer模型来自发表于AAAI21的一篇best paper《Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting》。Informer模型针对Transformer存在的一系列问题,如二次时间复杂度、高内存使用率以及Encoder-Decoder的结构限制&…
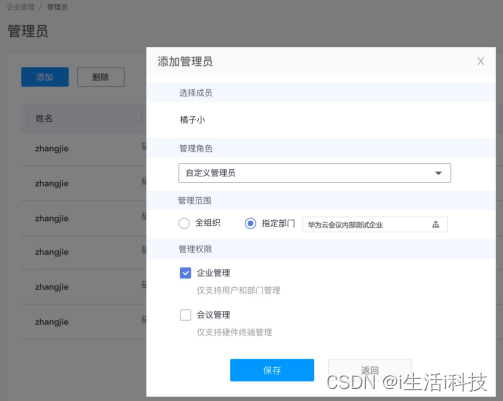
后台管理不可忽视,华为云会议最新支持管理员分权分域
如今,跨地域, 跨组织,需要随时随地接入的远程沟通协作变得愈加频繁,众多企业开始纷纷建设符合自身需求的智能会议室。在会议系统的众多能力中,后台管理,这项常常被C端用户忽略的能力,B端的企业却…
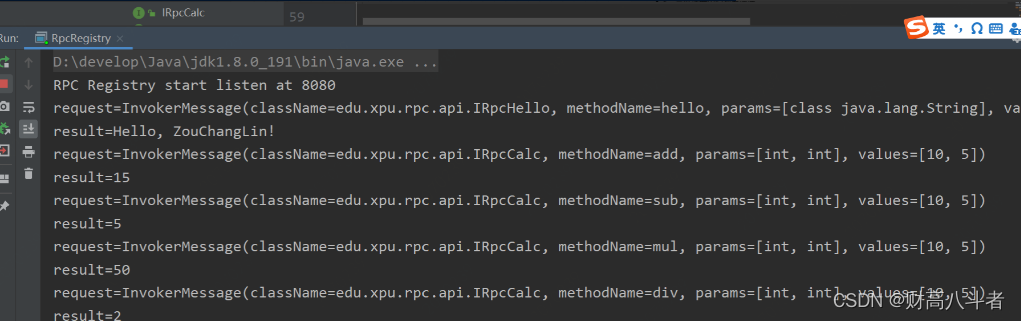
真的够可以的,基于Netty实现了RPC框架
RPC全称Remote Procedure Call,即远程过程调用,对于调用者无感知这是一个远程调用功能。目前流行的开源RPC 框架有阿里的Dubbo、Google 的 gRPC、Twitter 的Finagle 等。本次RPC框架的设计主要参考的是阿里的Dubbo,这里Netty 基本上是作为架构…
1. Spring Boot 3 入门学习教程之开发第一个 Spring Boot 应用程序
Spring Boot 3 入门学习教程之开发第一个 Spring Boot 应用程序0. 前言1. Spring Boot 介绍2. 系统要求2.1 Servlet容器2.2 GraalVM Native Image(GraalVM 原生镜像)3. 安装Spring Boot 开发环境3.1 安装JDK3.2 安装Spring Boot构建工具3.2.1 方式一&…
C++标准库分析总结(九)——<仿函数/函数对象>
目录
1.functor仿函数简介
2 仿函数的分类
3 仿函数使用
4 仿函数可适配的条件 1.functor仿函数简介
仿函数是STL中最简单的部分,存在的本质就是为STL算法部分服务的,一般不单独使用。仿函数(functors)又称为函数对象&…
【InnoDB Cluster】修改已有集群实例名称及成员实例选项
【InnoDB Cluster】修改已有集群实例名称,成员实例名称和选项 文章目录【InnoDB Cluster】修改已有集群实例名称,成员实例名称和选项修改名称修改已有集群实例名称修改已有集群实例的成员实例名称修改成员服务器操作系统的主机名直接修改元数据库中的表使…
力扣(LeetCode)88. 合并两个有序数组(C++)
朴素思想
朴素思想,开第三个数组,对 nums1nums1nums1 和 nums2nums2nums2 进行二路归并。
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {vector<int> nums3(mn);int i 0,j …
2.2 Linux启动初始化文件系统
为了方便了解和调试我们的Linux系统,我们需要将proc,debugfs,tmp等挂载起来,否则我们我发了解系统的进程,负载等信息,如下是未进行任何挂载时,我们无法通过ps等方法查看系统任何进程信息: 一,挂载proc fs
proc是一个伪文件系统,(伪文件系统只存在内存中,而不占用存…