l论文作者开发一个算法计算抽样S方程中使用
$$I(\mathbf{c},\mathbf{v})\approx {\hat{I}}_{\mathcal{S}}(\mathbf{c},\mathbf{v})=\sum _{i=1}^{m-1}{\hat{\tau }}_i{L}_i$$
首先是通过利用约束方程 :
$$\underset{t\in [0,M]}{\max }|O(t)-\hat{O}(t)|\le B_{\mathcal{T},\beta }=\underset{k\in [n-1]}{\max }\left\{\exp \left(-\hat{R}\left(t_k\right)\right)\left(\exp \left(\hat{E}\left(t_{k+1}\right)\right)-1\right)\right\},$$ 找到 样本 $\mathrm{T}$ 这样$\hat{0}$:
$$\hat{O}(t)=1-exp(-\hat{R}(t))$$
提供了一个$ϵ$近似真实的不透明度 $O$, 其中$ϵ$为超参数，即 $B_{T,\beta }<ϵ$.第二,我们执行逆CDF抽样与$\hat{O}$.

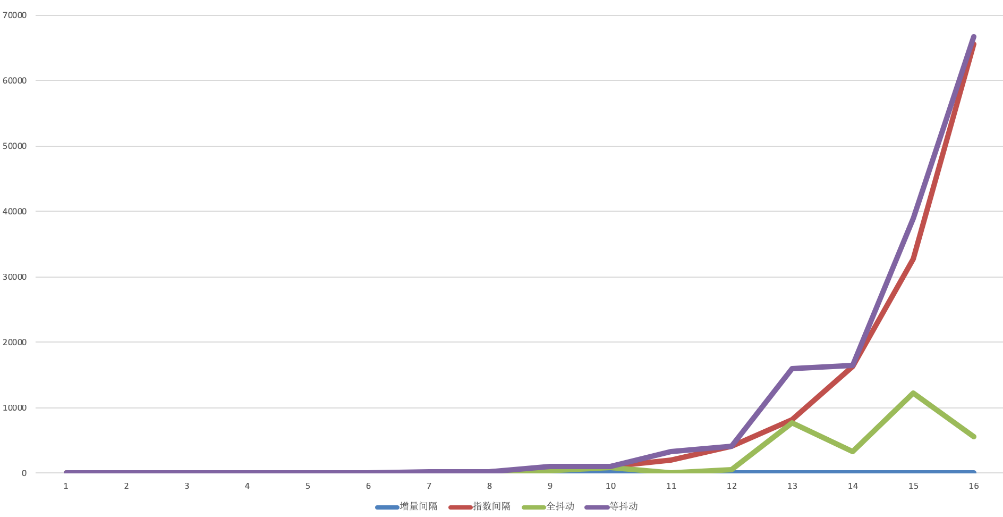
注意，从引理1可以得出，我们可以简单地选择足够大的n来保证$B_{T,\beta }<ϵ$。然而，这将导致过多的样本。相反，我们建议一个简单的算法来减少实际中所需的样本数量，并允许使用有限的样本点预算。简单地说，我们从均匀采样$T=T_0$开始，用引理2初始设置${\beta }_{+}>\beta$满足$B_{T,{\beta }_{+}}\le ϵ$。然后，我们重复上采样$T$以降低${\beta }_{+}$，同时维持$B_{T,{\beta }_{+}}\le ϵ$。尽管这个简单的策略不能保证收敛，但我们发现${\beta }_{+}$通常收敛于${\beta }_{+}$（通常为85%，见图3），即使在不收敛的情况下，算法提供的${\beta }_{+}$的不透明度近似仍然保持一个误差。算法如下所示（算法1）。

我们初始化$T$(1号线算法1)均匀采样 T 0 = { t i } i = 1 n , t k = ( k − 1 ) M n − 1 , k ∈ [ n ] T_0 = \{t_i\} ^n_{i = 1}, t_k = \frac{(k−1)M}{n−1}, k∈[n] T0​={ti​}i=1n​,tk​=n−1(k−1)M​,k∈[n](我们在我们的实现中使用n = 128)。给定这个采样，我们接下来根据引理2选取${\beta }_{+}>\beta$，使得误差界满足要求的界（算法1中的第2行）。

为了降低${\beta }_{+}$，同时保持$B_{T,{\beta }_{+}}\le ϵ$，将n个样本添加到T（算法1中的第4行），其中从每个间隔采样的点数与其当前误差界限成比例，公式：
$$\underset{t\in [t_k,t_{k+1}]}{\max }O(t)-\hat{O}(t)|\le exp(\hat{E}(t_{k+1})-1)$$
假设T被充分上采样并满足$B_{T,{\beta }_{+}}\le ϵ$，我们将${\beta }_{+}$向$\beta$减小。因为算法没有停止，所以我们有$B_{T,{\beta }_{+}}\ge ϵ$。因此，中值定理蕴含着存在$\beta \in （\beta ，{\beta }_{+}）$使得$B_{T,{\beta }_{+}}=ϵ$。我们使用二分法（最多10次迭代）来有效地搜索$\beta$并相应地更新${\beta }_{+}$（算法1中的第6行和第7行）。该算法迭代运行，直到$B_{T,{\beta }_{+}}\le ϵ$或达到最大迭代次数5。无论哪种方式，我们都使用最终的$T$和${\beta }_{+}$（保证提供$B_{T,{\beta }_{+}}\le ϵ$）来估计当前的不透明度$O$，算法1中的第10行）。最后，我们使用逆变换采样返回一个新的m = 64个样本O的集合（算法1中的第11行）。图3显示了算法1的定性说明，β = 0.001和= 0.1（典型值）。

引理1.固定$\beta >0$。对于任何$ϵ>0$，足够密集的采样T将提供$B_{T,{\beta }_{+}}\le ϵ$。其次，在样本数固定的情况下，我们可以设置$\beta$，使得误差界小于：$ϵ$.

引理2.固定$n>0$。对于任何$ϵ>0$，有一个足够大的$\beta$满足$$\beta \ge \frac{\alpha M^2}{a(n-1)log(1+ϵ)}$$将提供$B_{T,{\beta }_{+}}\le ϵ$.