题目来源
96. 不同的二叉搜索树
递归
1.我们要知道二叉搜索树的性质,对于一个二叉搜索树,其 【左边的节点值 < 中间的节点值 < 右边的节点值】,也就是说,对于一个二叉搜索树,其中序遍历之后形成的数组应该是一个递增的序列,如下图:

2.我们不妨就假设我们拿到了一个中序遍历的数组nums = [1,2,3,4,5,6,7],来思考一个这样的数组能延伸出多少种二叉搜索树。
首先,对于数组中的每一个元素,都有可能成为二叉树最顶部的root节点,例如上图中,是nums[4]这个值,即5,充当了root节点。
3.还拿5这个节点为例,即上图,其左边有四个节点,右边有两个节点。对于左边的四个节点,假设能延伸出 n 种二叉搜索树子树,对于右边的两个节点,假设能延伸出 m 种二叉搜索树子树。则以5为root节点时的二叉搜索树总数为 m*n
4.这样我们遍历刚刚的nums数组,以值i(注意不是下标)当做根节点,其左边有i-1个节点,右边有n-i个节点,计算出可能的二叉搜索树数量,添加到总结果里即可,我们初步写出的代码如下
class Solution {
public int numTrees(int n) {
if(n == 0 || n == 1){
return 1;
}
int count = 0;
for(int i = 1;i<=n;i++){
count+=numTrees(i-1)*numTrees(n-i);
}
return count;
}
}

递归优化
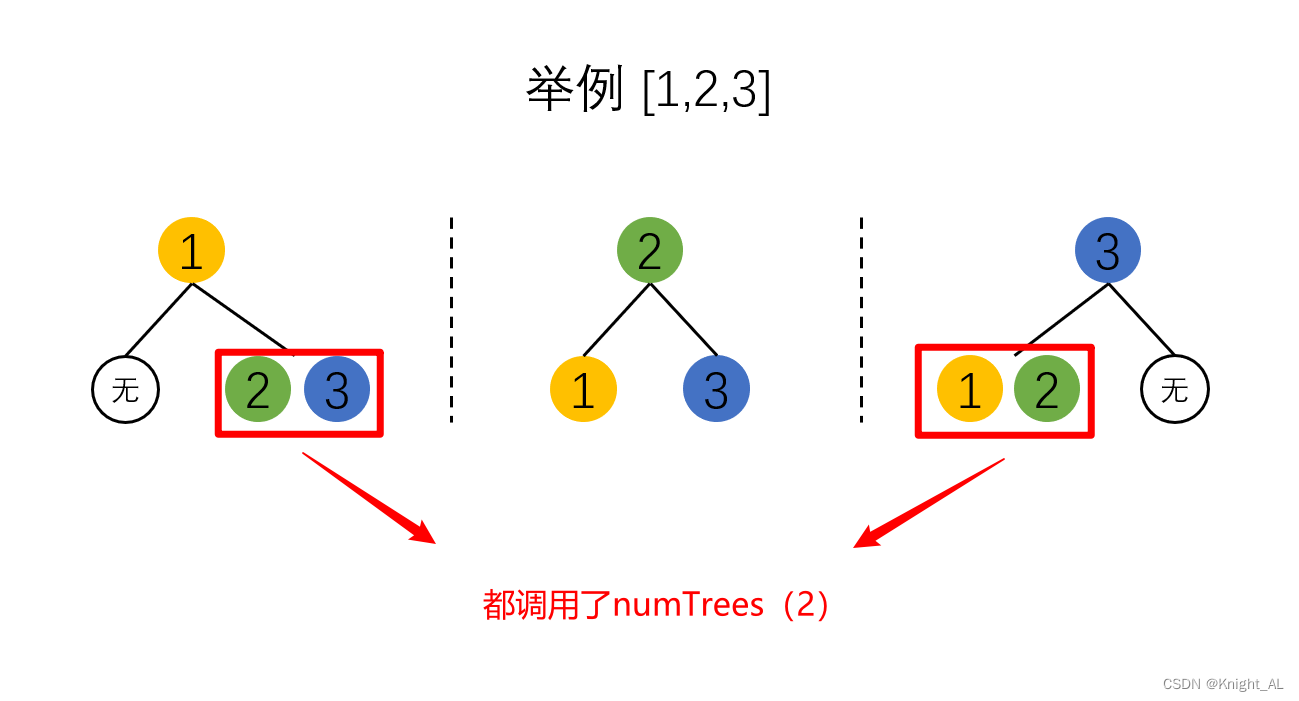
其实是出现了很多次重复计算过程,举例[1,2,3]
大量的重复计算造成我们时间过长,因此我们可以用一个HashMap存储n和子树数量的映射,如果已经计算过了当前n的子树数量,直接取出用即可
class Solution {
private HashMap<Integer,Integer> map = new HashMap();
public int numTrees(int n) {
if(n == 0 || n == 1){
return 1;
}
if(map.containsKey(n)){
return map.get(n);
}
int count = 0;
for(int i = 1;i<=n;i++){
count+=numTrees(i-1) * numTrees(n-i);
map.put(n,count);
}
return count;
}
}

动态规划
动规五部曲
- 1.确定dp数组(dp table)以及下标的含义
dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ,都是一样的。
- 2.确定递推公式
在上面的分析中,其实已经看出其递推关系, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
- 3.dp数组如何初始化
初始化,只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。
那么dp[0]应该是多少呢?
从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。
从递归公式上来讲,dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。
所以初始化dp[0] = 1
- 4.确定遍历顺序
首先一定是遍历节点数,从递归公式:dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i里面每一个数作为头结点的状态,用j来遍历。
for(int i = 1;i <= n;i++){
for(int j = 1;j<=i;j++){
dp[i] += dp[j-1]*dp[i-j];
}
}
- 5.举例推导dp数组
n为5时候的dp数组状态如图:
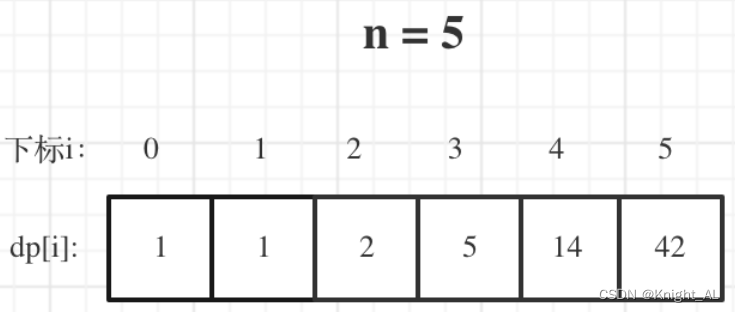
整体代码
class Solution {
public int numTrees(int n) {
int[] dp = new int[n+1];
dp[0] = 1;
for(int i = 1;i <= n;i++){
for(int j = 1;j<=i;j++){
dp[i] += dp[j-1]*dp[i-j];
}
}
return dp[n];
}
}