题目：剑指 Offer 34. 二叉树中和为某一值的路径 - 力扣（Leetcode）

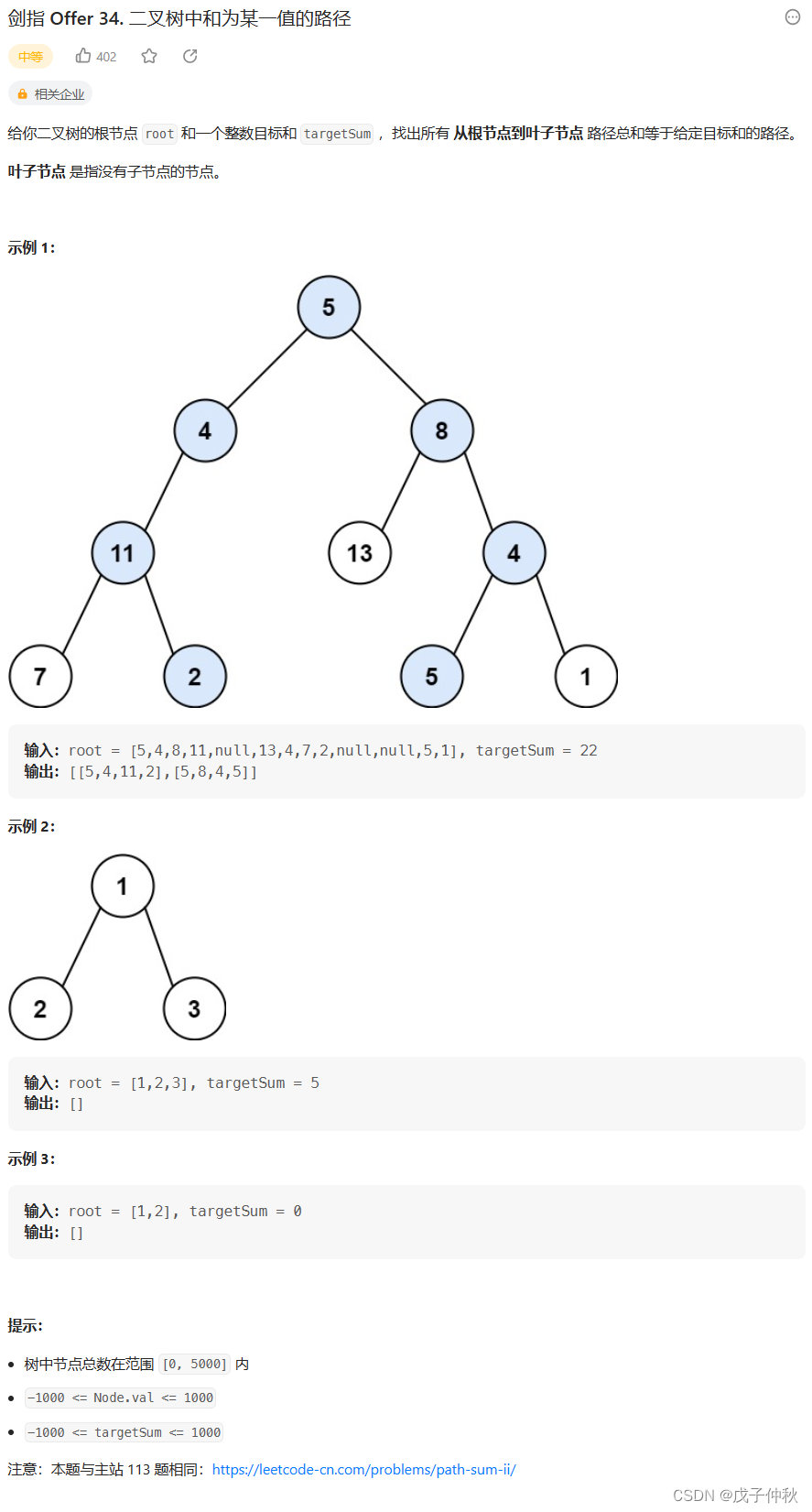
题目的接口：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> pathSum(TreeNode* root, int target) {
        
    }
};

解题思路：

这道题我一看到题目，

我立马就想到是dfs，也就是深度优先搜索，

思想就是递归搜索整个二叉树的每一个节点，

记录，将路径记录到数组中，

求和，计算每一个通向叶子节点的路径的节点和，

然后与题目中给出的taget进行比较，

如果已经走到叶子节点并且路径的节点和与taget相同，

就将路径的记录塞进二维数组，

然后退回到上一节点，路径记录减一，

以此类推。

最后返回二维数组即可。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> v;
    vector<vector<int>> vv;

    //传一个sum用来计算路径的节点和
    void dfs(TreeNode* node, int target, int sum)
    {
        //计算路径节点和
        sum += node->val;

        //将路径记录
        v.push_back(node->val);

        //如果左孩子不为空，继续搜索
        if(node->left)
        {
            dfs(node->left, target, sum);
        }

        //如果右孩子不为空，继续搜索
        if(node->right)
        {
            dfs(node->right, target, sum);
        }

        //如果路径节点和与taget相等，且已经走到了叶子节点
        if(sum == target && node->left == nullptr && node->right == nullptr)
        {
            //将成功匹配的路径值放进二维数组中
            vv.push_back(v);
        }

        //搜索退回上一级节点，路径记录数组也删除最后一个节点的值
        v.pop_back();
    }

    vector<vector<int>> pathSum(TreeNode* root, int target) {
        //如果是空树，就直接返回空数组
        if(!root)
        {
            return vv;
        }

        //深度优先搜索
        dfs(root, target, 0);

        //返回符合条件的数组
        return vv;
    }
};