XGBoost算法原理详解与参数详解

R语言XGBoost参数详解

1. XGBoost线性模型的实现

前面文章中已经详细的介绍了XGBoost基于决策树的实现，今天我们主要介绍XGBoost基于线性模型的实现。
我们主要介绍简单的三种线性模型：Lasso、Ridge、弹性网。
Lasso:采用了L1正则化的惩罚，目标函数为$\mathcal{J}(\omega )={\sum }_{i=1}^m(y_i-{\omega }^T{X}_i{)}^2+\lambda {\sum }_{j=1}^n{\omega }_j^2$.
Ridge:采用了L2正则化的惩罚，目标函数为$\mathcal{J}(\omega )={\sum }_{i=1}^m(y_i-{\omega }^T{X}_i{)}^2+\lambda {\sum }_{j=1}^n\left|{\omega }_j\right|$.
弹性网：结合了L1与L2正则项的惩罚，目标函数为$\mathcal{J}(\omega )={\sum }_{i=1}^m(y_i-{\omega }^T{X}_i{)}^2+{\lambda }_1{\sum }_{j=1}^n{\omega }_j^2+{\lambda }_2{\sum }_{j=1}^n\left|{\omega }_j\right|$.

线性模型通过学习特征的线性组合进行预测，即：$$y={\omega }^{T}X+\beta ,{\omega }^T=({\omega }_1,{\omega }_2,{\omega }_3,...,{\omega }_m)$$
$m$为特征的数量，模型的训练即为确定参数$\omega$与$\beta$.
XGBoost线性模型的目标函数定义为：
$$Ob{j}^{(s)}=\frac{1}{n}\sum _{i=1}^{n}L(y_i,{\hat{y}}_i^{(s)})+\Omega (\omega ,\beta )$$.
其中${\hat{y}}_i^{(s)}$为第$i$个样本在模型$s$轮时得到的预测值；$y_i$为第$i$个样本的真实值；$L$为损失函数；$\Omega$为正则化项。

这里的正则化项$\Omega$采用了弹性网的惩罚方式：$$\Omega (\omega ,\beta )=\frac{1}{2}\lambda \sum _{j=1}^m{\omega }_j^2+\frac{1}{2}{\lambda }_{\beta }{\beta }^2+\alpha \sum _{j=1}^m\left|{\omega }_j\right|$$.
由于向量乘积满足分配律，所以对于线性模型的参数进行如下的改写：
$${\omega }_s^{T}X+{\beta }_s=({\omega }_{s-1}^T+\Delta {\omega }^T)X+{\beta }_{s-1}+\Delta \beta$$
其中${\omega }_s^T$为第$s$轮训练时的参数；${\omega }_{s-1}^T$为$s-1$轮的参数；$\Delta \omega$为先后两轮训练中$\omega$的变化；${\beta }_s$与${\beta }_{s-1}$为前后两轮训练中的截距项；$\Delta \beta$为两轮训练下截距项的变化。所以目标函数可写为：
$$Ob{j}^{(s)}=\frac{1}{n}\sum _{i=1}^{n}L(y_i,{\hat{y}}_i^{(s-1)}+\Delta {\omega }^T{x}_i+\Delta \beta )+\Omega (\omega ,\beta )$$.
$$\begin{array}{rl}Ob{j}^{(s)}& =\frac{1}{n}\sum _{i=1}^{n}L(y_i,{\hat{y}}_i^{(s-1)}+\Delta {\omega }^T{x}_i+\Delta \beta )+\Omega (\omega ,\beta )\\ & \approx \frac{1}{n}\sum _{j=1}^m\sum _{i=1}^n[L(y_i,{\hat{y}}^{(s-1)}+\Delta \beta )+g_i(\Delta {\omega }_j{x}_{ij})+\frac{1}{2}{h}_i(\Delta {\omega }_j{x}_{ij}{)}^2]+\frac{1}{2}\lambda \sum _{j=1}^m({\omega }_{(s-1)j}+\Delta {\omega }_j{)}^2+\frac{1}{2}{\lambda }_{\beta }{\beta }^2+\alpha \sum _{j=1}^m\left|{\omega }_{(s-1)j}+\Delta {\omega }_j\right|\end{array}$$

上式和XGBoost对CART的优化方式相同：二阶泰勒展开。
此时上述的目标函数相当于一个以$\Delta {\omega }_j$为自变量的一元二次函数，判读${\omega }_{(s-1)j}+\Delta {\omega }_j$与$0$的大小关系，再根据一元二次函数最值公式求出$\Delta {\omega }_j$的最优值。

若${\omega }_{(s-1)j}+\Delta {\omega }_j\ge 0$,$\Delta {\omega }_j=\max (-\frac{{\sum }_{i=1}^n{g}_i{x}_{ij}+\lambda {\omega }_{(s-1)j}+\alpha }{{\sum }_{i=1}^n{h}_i{x}_{ij}^2+\lambda },-{\omega }_{(s-1)j})$.
若${\omega }_{(s-1)j}+\Delta {\omega }_j<0$,$\Delta {\omega }_j=\min (-\frac{{\sum }_{i=1}^n{g}_i{x}_{ij}+\lambda {\omega }_{(s-1)j}-\alpha }{{\sum }_{i=1}^n{h}_i{x}_{ij}^2+\lambda },-{\omega }_{(s-1)j})$.
对于截距项$\beta$采用上述方法求解得到：
$$\Delta \beta =-\frac{{\sum }_{i=1}^n{g}_i+{\lambda }_{\beta }{\beta }_{(s-1)}}{{\sum }_{i=1}^n{h}_i+{\lambda }_{\beta }}$$.

以上就是XGBoost线性模型实现的步骤以及参数的优化求解。

2.XGBoost对二分类和多分类的处理方法

问题：

我想关于XGBoost算法的原理以及理论证明大家在论文、书籍以及相关的博客上应该都可以看懂，可能对XGBoost如何解决分类等问题不是很清楚，比如二分类问题下XGBoost的输出概率值是如何做到的？这个问题如果理解了大家对XGBoost解决问题的逻辑就会十分明了。

以R语言自带的数据集agaricus为例进行二分类.

> library(xgboost)
> data(agaricus.train, package='xgboost')
> 
> bst <- xgboost(data = agaricus.train$data, label = agaricus.train$label, max_depth = 3,
+                eta = 1, nthread = 2, nrounds = 2,objective = "binary:logistic")
[1]     train-logloss:0.161178 
[2]     train-logloss:0.064728 
> 
> 
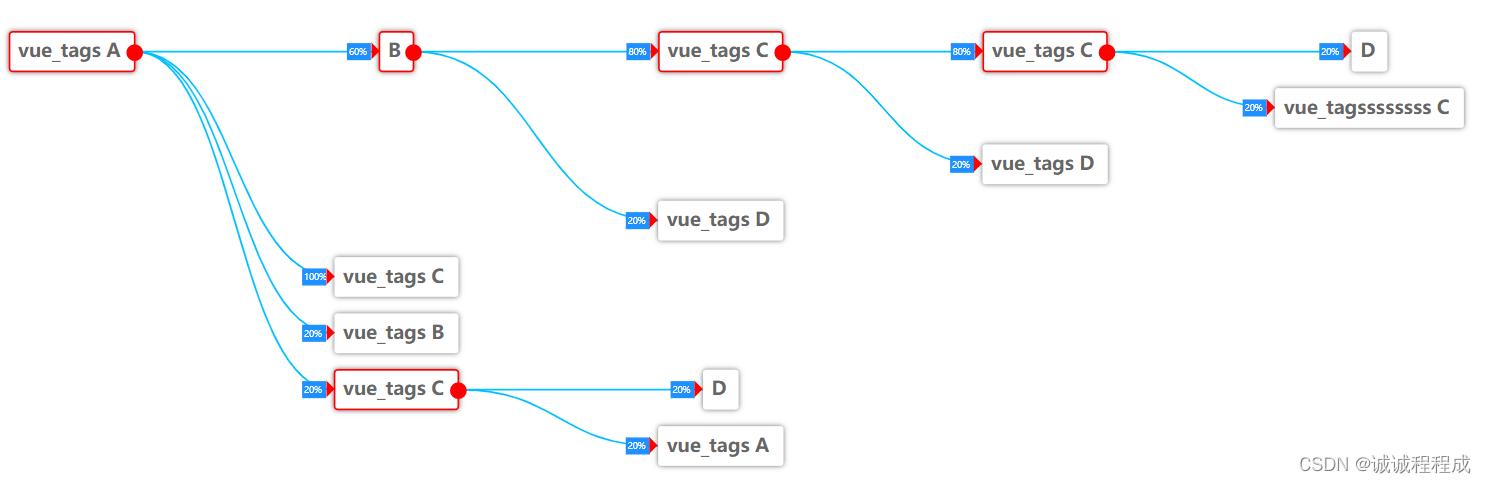
> xgb.plot.tree(model = bst) # 可视化xgboost生成的树模型

以上图片对于agaricus数据集生成了两颗树模型，XGboost在预测测试集的输出概率时会把测试集的样本按照树模型的划分规则分别使其落入Tree0与Tree1的叶节点上. 比如测试集中的样本1在Tree0与Tree1的叶节点上的value进行相加，然后通过Sigmoid激活函数转换为测试集中正类标签的预测概率.
以下为上述的验证部分：通过对Tree0与Tree1的叶子节点的值进行排列后求和，然后通过Sigmoid激活函数转为概率输出值；另一部分对测试集进行了概率预测. 自然而然地对测试集进行了概率预测应该是上述过程的子集.

> print(xgb.dump(bst, with_stats = TRUE))
 [1] "booster[0]"                                                                    
 [2] "0:[f28<-9.53674316e-07] yes=1,no=2,missing=1,gain=4000.53101,cover=1628.25"    
 [3] "1:[f55<-9.53674316e-07] yes=3,no=4,missing=3,gain=1158.21204,cover=924.5"      
 [4] "3:[f59<-9.53674316e-07] yes=7,no=8,missing=7,gain=568.215576,cover=812"        
 [5] "7:leaf=1.90174532,cover=772.5"                                                 
 [6] "8:leaf=-1.95061731,cover=39.5"                                                 
 [7] "4:[f20<-9.53674316e-07] yes=9,no=10,missing=9,gain=114.297333,cover=112.5"     
 [8] "9:leaf=1.77777779,cover=8"                                                     
 [9] "10:leaf=-1.98104262,cover=104.5"                                               
[10] "2:[f108<-9.53674316e-07] yes=5,no=6,missing=5,gain=198.173828,cover=703.75"    
[11] "5:[f66<-9.53674316e-07] yes=11,no=12,missing=11,gain=86.3969727,cover=690.5"   
[12] "11:leaf=-1.98531032,cover=679.75"                                              
[13] "12:leaf=0.808510661,cover=10.75"                                               
[14] "6:leaf=1.85964918,cover=13.25"                                                 
[15] "booster[1]"                                                                    
[16] "0:[f28<-9.53674316e-07] yes=1,no=2,missing=1,gain=480.158417,cover=719.00769"  
[17] "1:[f20<-9.53674316e-07] yes=3,no=4,missing=3,gain=276.744751,cover=414.977539" 
[18] "3:leaf=1.14570117,cover=296.038025"                                            
[19] "4:[f35<-9.53674316e-07] yes=7,no=8,missing=7,gain=392.998077,cover=118.939491" 
[20] "7:leaf=-6.8755784,cover=8.36453247"                                            
[21] "8:leaf=-0.127376497,cover=110.574959"                                          
[22] "2:[f108<-9.53674316e-07] yes=5,no=6,missing=5,gain=28.7784424,cover=304.030151"
[23] "5:[f38<-9.53674316e-07] yes=9,no=10,missing=9,gain=26.1188354,cover=297.850983"
[24] "9:leaf=-0.0386054367,cover=22.8540649"                                         
[25] "10:leaf=-1.15275192,cover=274.996918"                                          
[26] "6:leaf=0.994743764,cover=6.17916679" 
> tree0 = c(1.90174532, -1.95061731, 1.77777779, -1.98104262, -1.98531032, 0.808510661,
+           1.85964918)
> 
> tree1 = c(1.14570117, -6.8755784, -0.127376497, -0.0386054367, -1.15275192, 0.994743764)
> 
> 
> df = expand.grid(tree0,tree1)
> 
> 
> f = function(x)  1 / (1 + exp(-sum(x)))  
> 
> pred1 = round(apply(df, 1, f),4)
> 
> data(agaricus.test, package='xgboost')
> pred2 = round(predict(bst, agaricus.test$data),4)
> length(unique(pred2))
[1] 11
> 
> all(unique(pred2) %in% unique(pred1)) # 成立
[1] TRUE
 

以上就是XGBoost个人想到的一些细节补充，本片内容到此为止.