0104路径搜索和单点路径-无向图-数据结构和算法(Java)

news2024/11/27 6:38:08

文章目录

- 2 单点路径
- 2.1 API
- 2.2 算法实现
- 后记

2 单点路径

单点路径。给定一幅图和一个起点s，回答“从s到给定的目的顶点v是否存在一条路径？如果有，找出这条路径。”等类似问题。

2.1 API

单点路径问题在图的处理邻域中十分重要。根据标准设计模式，给出以下API：

public class	Paths
	Paths(Graph g, int s)	G中找出所有起点为s的路径
boolean	hasPathTo(int v)	是否存在从s到v的路径
Iterable<Integer>	pathTo(int v)	s到v的路径，如果不存在返回null

2.2 算法实现

使用深度优先搜索搜索图中的路径非递归算法实现，源代码2.2-1如下所示：

package com.gaogzhen.datastructure.graph.undirected;

import com.gaogzhen.datastructure.stack.Stack;
import edu.princeton.cs.algs4.Graph;
import edu.princeton.cs.algs4.In;

import java.util.Iterator;
import java.util.Map;

/**
 * 单点连通性
 * @author: Administrator
 * @createTime: 2023/03/03 19:58
 */
public class DepthFirstPaths {
    /**
     * 顶点是否标记
     */
    private boolean[] marked;

    /**
     * 从起点到一个顶点的已知路径上的最后一个顶点
     */
    private int[] edgeTo;

    /**
     * 图
    */
    private Graph graph;

    /**
     * 起点
     */
    private int s;

    public DepthFirstPaths(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        int v = graph.V();
        check(s);
        marked = new boolean[v];
        edgeTo = new int[v];
        dfs();
    }

    /**
     * 搜索图g以v为起点的路径
     */
    private void dfs() {
        Stack<Entry<Integer, Iterator<Integer>>> path = new Stack<>();
        // marked[v] = true;
        if (!marked[s]) {
            // 键值对起点-起点对应邻接表迭代器压入栈中
            marked[s] = true;
            Iterable<Integer> iterable = graph.adj(s);
            Iterator<Integer> it;
            if (iterable != null && (it = iterable.iterator()) != null){
                path.push(new Entry<>(s, it));
            }
        }
        while (!path.isEmpty()) {
            Entry<Integer, Iterator<Integer>> entry = path.pop();
            int x;
            Iterator<Integer> it = entry.getValue();
            Integer f = entry.getKey();
            while (it.hasNext()) {
                // 当前顶点对应的邻接表迭代器还有元素，获取下一个元素
                x = it.next();
                if (!marked[x]) {
                    // 顶点未被标记，标记顶点且标记路径x->f
                    // f是x所在邻接表对应的顶点
                    marked[x] = true;
                    edgeTo[x] = f;
                    if (it.hasNext()) {
                        // 邻接表迭代器还有元素，重新压入栈
                        path.push(entry);
                    }
                    // 按照深度优先原则，把新标记顶点对应的键值对压入栈中，在下次循环时优先访问
                    Iterable<Integer> iterable = graph.adj(x);
                    if (iterable != null && (it = iterable.iterator()) != null){
                        path.push(new Entry<>(x, it));
                    }
                    break;
                }
            }

        }
    }

    /**
     * 检测索引是否在范围之内
     * @param i 给定索引
     */
    private void check(int i) {
        if (i < 0 || i > graph.V() - 1) {
            throw new IndexOutOfBoundsException("索引越界异常");
        }
    }

    /**
     * 判断是否存在起点s到v的路径
     * @param x 给定顶点
     * @return
     */
    public boolean hashPathTo(int x) {
        check(x);
        return marked[x];
    }

    /**
     * s到v的路径，如果不存在返回null
     * @param x 指定的顶点
     * @return  起点到指定顶点的路径
     */
    public Iterable<Integer> pathTo(int x) {
        // 判断v和起点间是否存在路径
        if (!hashPathTo(x)) {
            // 不存在返回null
            return null;
        }
        // 栈记录x到起点的路径
        Stack<Integer> path = new Stack<>();
        // edge[]是一棵父链接表示的树，所以从已知路径的最后一个顶点开始沿父链接遍历，直到起点
        for (int p = x; p != s; p = edgeTo[p]) {
            path.push(p);
        }
        // 加入起点
        path.push(s);
        return path;
    }

}

测试：

    public static void testPaths() {
        String path = "H:\\gaogzhen\\java\\projects\\algorithm\\asserts\\maze.txt";
        In in = new In(path);
        Graph graph = new Graph(in);
        int s = 0;
        DepthFirstPaths depthFirstPaths = new DepthFirstPaths(graph, s);

        int v = 4;
        System.out.println(depthFirstPaths.hashPathTo(v));
        System.out.println(depthFirstPaths.pathTo(v));
    }
   // 测试结果
   true
[0, 2, 3, 5]

算法分析：

该算法基于深度优先搜索实现的，可以参考上一篇 0103深度优先搜索和单点连通-无向图-数据结构和算法(Java)
这里添加了一个实例变量edgeTo[]整形数组，用来记录从每个与s连通的顶点回到起点s的路径。
在由边v-w第一次访问任意顶点w时，将edgeTo[w]设置为v来记住这条路径。换句话说，v-w是从s到w的路径上的最后一条已知的便。
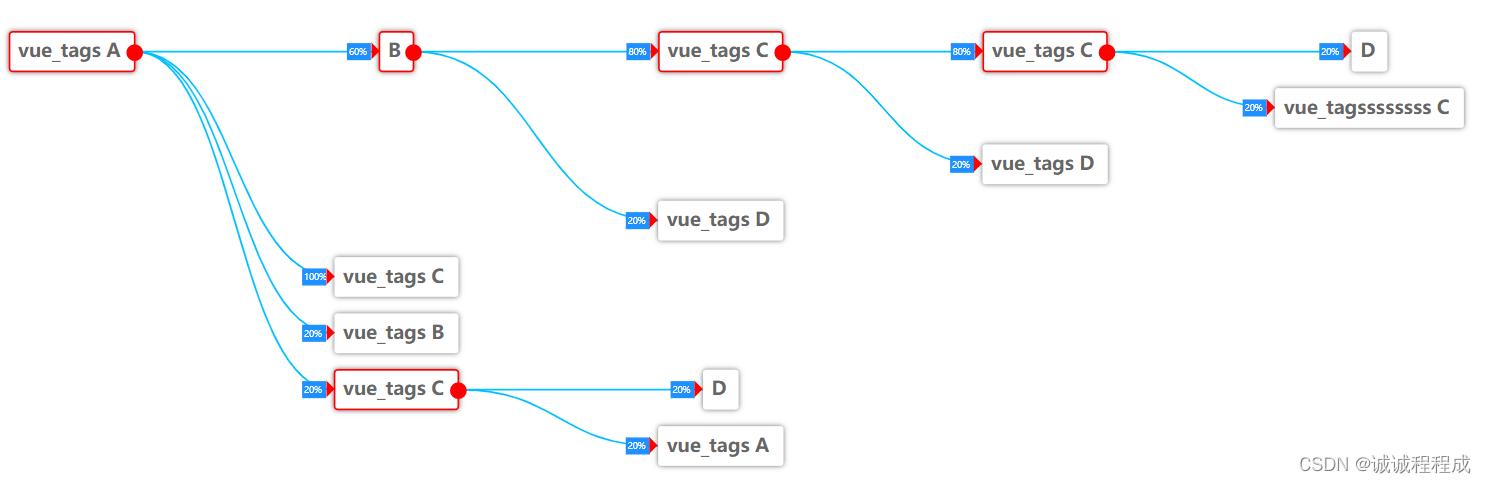
搜索的结果是一棵以起点为根结点的树，edgeTo[]是一棵由父链接表示的树。如下图所示：
pathTo()通过x自下沿路径向上遍历整棵树，x设为edgeTo[x]，将经过的顶点压入栈中，返回Iterable对象帮助用例遍历s到v的路径。
- edgeTo[]是一棵由父链接表示的树,x=edgeTo[x]保证向上遍历