模式识别 —— 第二章 参数估计
文章目录
- 模式识别 —— 第二章 参数估计
- 最大似然估计(MLE)
- 最大后验概率估计(MAP)
- 贝叶斯估计
最大似然估计(MLE)
在语言上:
- 似然(likelihood)和**概率(probability)**是同义词,都指事件发生的可能性。
但是在统计中:
- 概率是已知参数,对结果可能性的预测。
- 似然是已知结果,对参数是某个值的可能性预测。
可见这两个过程正好是相反的。
因此最大似然估计是已知数据来求概率最大的参数。
以抛硬币为例,假设我们有一枚硬币,现在要估计其正面朝上的概率 θ \theta θ。我们进行了10次实验其中正面朝上的次数为6次,反面朝上的次数为4次。
对一个独立同分布的样本集来说,总体的似然就是每个样本似然的乘积。针对抛硬币的问题,似然函数可写作:
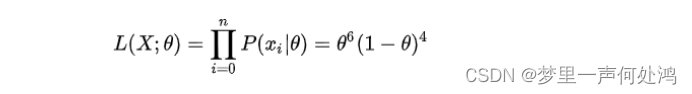
似然函数图如下:
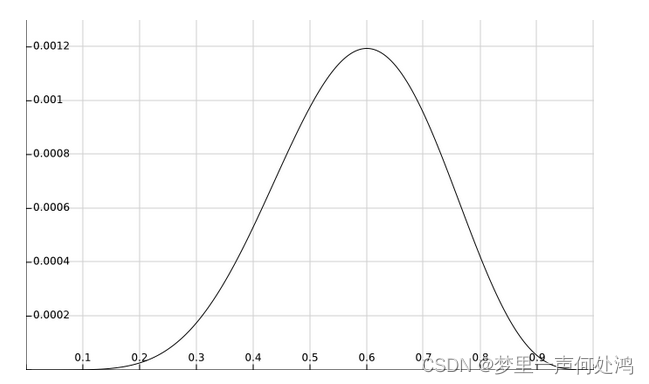
由于总体的似然就是每个样本似然的乘积,为了求解方便,我们通常会将似然函数转成对数似然函数,然后再求解。可以转成对数似然函数的主要原因是对数函数并不影响函数的凹凸性。因此上式可变为:
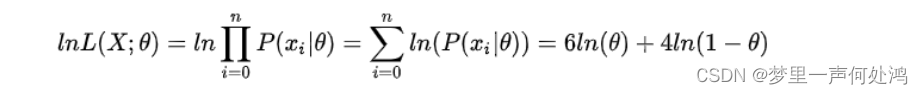
对该式子求导等于0即可解出当
θ
^
=
0.6
\hat{\theta} = 0.6
θ^=0.6时,是最优参数。
正态分布的最大似然估计
假设样本服从正态分布
N
N
N~
(
μ
,
σ
2
)
(\mu,\sigma^2)
(μ,σ2),则其似然函数为:
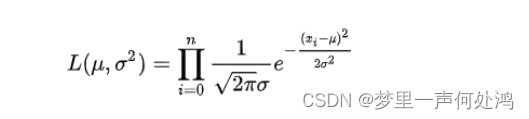
对其取对数得:
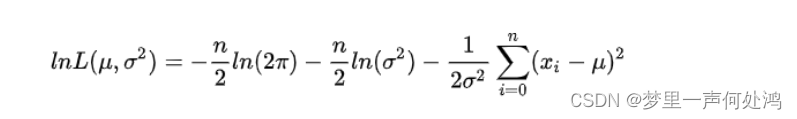 分别对
μ
,
σ
2
\mu , \sigma^2
μ,σ2求偏导,并令偏导数为0,得:
分别对
μ
,
σ
2
\mu , \sigma^2
μ,σ2求偏导,并令偏导数为0,得:
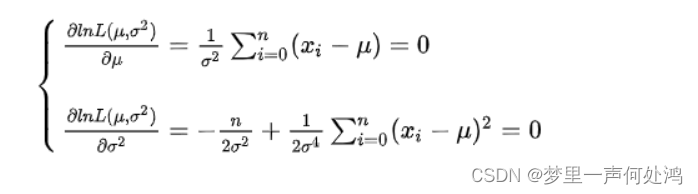
解得:
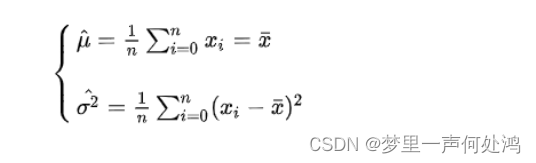
最大似然估计的求解步骤: \red{最大似然估计的求解步骤:} 最大似然估计的求解步骤:
- 确定似然函数
- 将似然函数转化为对数似然函数
- 求对数似然函数的最大值(求导,解似然方程)
最大后验概率估计(MAP)
最大似然估计认为使似然函数 P ( X ∣ θ ) P(X\mid \theta) P(X∣θ)最大的 θ \theta θ就是最好的参数 θ \theta θ。此时最大似然估计是将 θ \theta θ看作固定的值,只是其值未知。
最大后验概率认为 θ \theta θ是一个随机变量 θ \theta θ,即具有某种概率分布,称为先验分布,求解时除了要考虑似然函数 P ( X ∣ θ ) P(X\mid \theta) P(X∣θ)之外还要考虑 θ \theta θ的先验分布 P ( θ ) P( \theta) P(θ)。其认为 P ( X ∣ θ ) P ( θ ) P(X\mid \theta)P( \theta) P(X∣θ)P(θ)取最大时的 θ \theta θ才是最优参数。
由于 X X X的先验分布 P ( X ) P( X) P(X)是固定的,所以其不影响对参数 θ \theta θ的判断。因此最大后验概率估计的公式表示为:
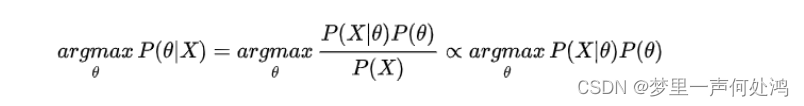 在抛硬币的例子中,通常认为当
θ
=
0.5
\theta = 0.5
θ=0.5时可能性最大。因此我们用均值为0.5,方差为0.1的高斯分布来描述
θ
\theta
θ的先验概率分布。其表达式如下:
在抛硬币的例子中,通常认为当
θ
=
0.5
\theta = 0.5
θ=0.5时可能性最大。因此我们用均值为0.5,方差为0.1的高斯分布来描述
θ
\theta
θ的先验概率分布。其表达式如下:
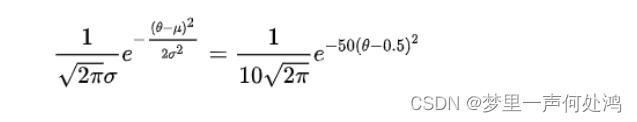
先验分布的函数如图:
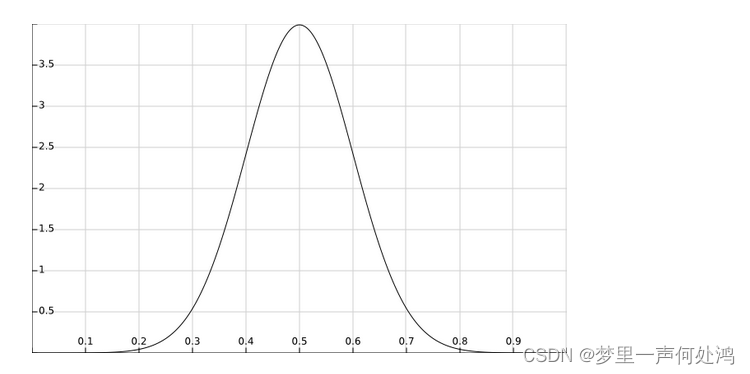
因此,先验与似然的乘积如下:
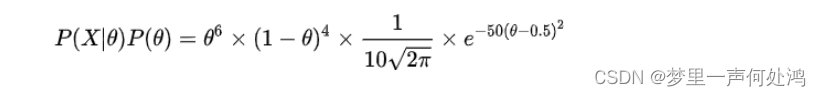 为了方便求导,我们将其转化为对数函数:
为了方便求导,我们将其转化为对数函数:
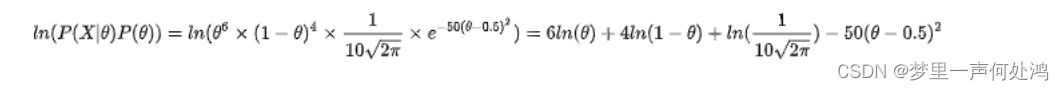
让上式为0化简得:
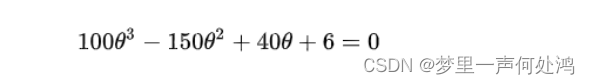
解得, θ ^ ≈ 0.529 \hat{\theta} \approx 0.529 θ^≈0.529
相比最大似然估计的 θ ^ = 0.6 \hat{\theta} = 0.6 θ^=0.6,可见在最大后验概率估计中 θ \theta θ的估计值与 θ \theta θ的先验分布有的很大的关系。
最大后验概率估计的求解步骤: \red{最大后验概率估计的求解步骤:} 最大后验概率估计的求解步骤:
- 确定参数的先验分布以及似然函数
- 将其乘积转换为对数形式
- 求对数函数的最大值(求导,解方程)
贝叶斯估计
贝叶斯估计是最大后验概率估计(MAP)的进一步扩展。
区别:贝叶斯估计并不是直接估计出 θ \theta θ的某个特定值,而是估计 θ \theta θ的分布
贝叶斯公式:
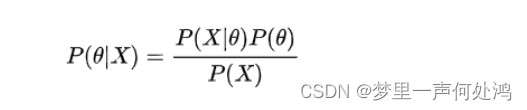
这里的
P
(
x
)
P(x)
P(x)是不可忽略的。在连续随机变量中,由于
P
(
x
)
=
∫
θ
P
(
X
∣
θ
)
P
(
θ
)
d
θ
P(x)=\int_\theta {P(X\mid\theta)P(\theta)} \,{\rm d}\theta
P(x)=∫θP(X∣θ)P(θ)dθ
因此贝叶斯公式变化为:
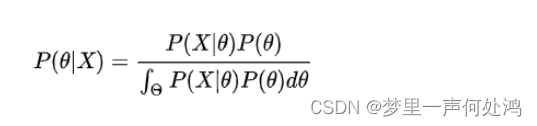 从上面的公式中可以看出,贝叶斯估计的求解非常复杂,因此选择合适的先验分布就非常重要。一般来说,计算积分
P
(
x
)
=
∫
θ
P
(
X
∣
θ
)
P
(
θ
)
d
θ
P(x)=\int_\theta {P(X\mid\theta)P(\theta)} \,{\rm d}\theta
P(x)=∫θP(X∣θ)P(θ)dθ是不可能的。
从上面的公式中可以看出,贝叶斯估计的求解非常复杂,因此选择合适的先验分布就非常重要。一般来说,计算积分
P
(
x
)
=
∫
θ
P
(
X
∣
θ
)
P
(
θ
)
d
θ
P(x)=\int_\theta {P(X\mid\theta)P(\theta)} \,{\rm d}\theta
P(x)=∫θP(X∣θ)P(θ)dθ是不可能的。
对于这个抛硬币的例子来说,如果使用共轭先验分布,就可以更好的解决这个问题。二项分布参数的共轭先验是Beta分布。由于 θ \theta θ的似然函数服从二项分布,因此在贝叶斯估计中,假设 θ \theta θ的先验分布服从 P ( θ ) ∽ B e t a ( α , β ) P(\theta)\backsim Beta(\alpha,\beta) P(θ)∽Beta(α,β)。 α \alpha α代表正确的次数, β \beta β代表错误的次数。
Beta分布的概率密度公式为:
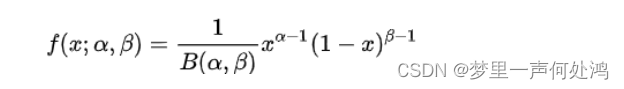 因此,贝叶斯公式可写为:
因此,贝叶斯公式可写为:
 这里
这里
假设,
α
=
3
,
β
=
3
\alpha = 3,\beta = 3
α=3,β=3。这种情况下,先验概率会在0.5处取得最大。对于贝叶斯估计
P
(
θ
∣
X
)
∽
B
e
t
a
(
θ
∣
9
,
7
)
P(\theta \mid X)\backsim Beta(\theta \mid 9,7)
P(θ∣X)∽Beta(θ∣9,7),这里我们得到的是估计参数
θ
\theta
θ的分布函数曲线为:

根据Beta分布的数学期望公式
E
(
θ
)
=
α
α
+
β
E(\theta) = \frac{\alpha}{\alpha+\beta} \quad
E(θ)=α+βα可得: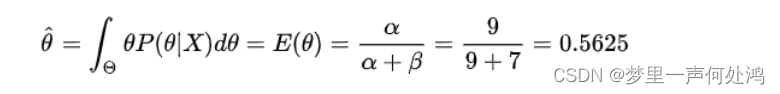
从最大似然估计、最大后验概率估计到贝叶斯估计,从下表可以看出
θ
\theta
θ的估计值
θ
^
\hat\theta
θ^是逐渐接近0.5的。从公式的变化可以看出,使用的信息是逐渐增多的。
最大似然估计、最大后验概率估计中都是假设 θ \theta θ未知,但是是一个确定的值,都将使函数取得最大值的 θ \theta θ作为估计值。区别在于最大化的函数不同,最大后验概率估计使用了 θ \theta θ的先验概率。
而在贝叶斯估计中,假设参数 θ \theta θ是未知的随机变量,不是确定值,求解的是参数 θ \theta θ在样本 X X X上的后验分布。