1 人工神经网络的历史
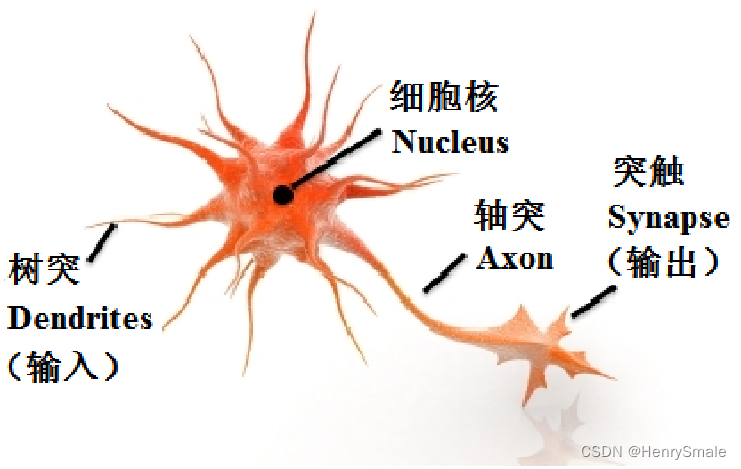
1.1 生物模型
1943年,心理学家W.S.McCulloch和数理逻辑学家W.Pitts基于神经元的生理特征,建立了单个神经元的数学模型(MP模型)。
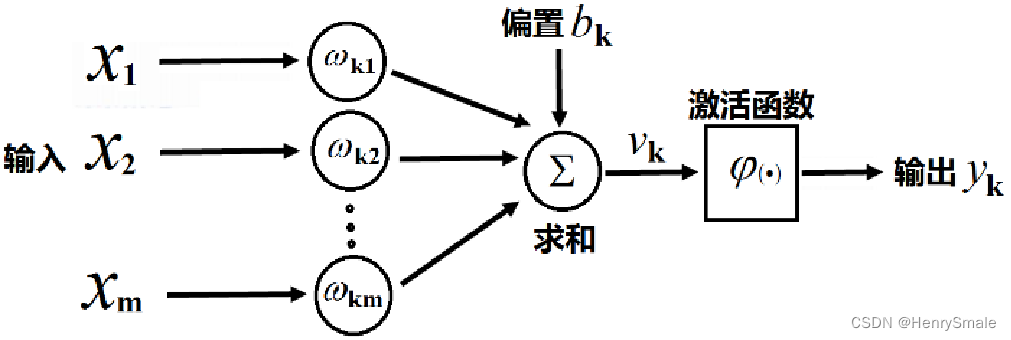
1.2 数学模型
y
k
=
φ
(
∑
i
=
1
m
ω
k
i
x
i
+
b
k
)
=
φ
(
W
k
T
X
+
b
)
y_{k}=\varphi\left(\sum_{i=1}^{m} \omega_{k i} x_{i}+b_{k}\right)=\varphi\left(W_{k}^{T} X+b\right)
yk=φ(i=1∑mωkixi+bk)=φ(WkTX+b)
1.3 感知器
1957年,Frank Rosenblatt从纯数学的度重新考察这一模型,指出能够从一些输入输出对
(
X
,
y
)
(X, y)
(X,y)中通过学习算法获得权重
W
W
W和
b
b
b 。
问题:给定一些输入输出对
(
X
,
y
)
(X, y)
(X,y),其中
y
=
±
1
y = \pm 1
y=±1,求一个函数,使
f
(
X
)
=
y
f(X) = y
f(X)=y。
感知器算法:设定
f
(
X
)
=
s
i
g
n
(
W
T
X
+
b
)
f(X) = sign (W^T X + b)
f(X)=sign(WTX+b),从一堆输入输出中自动学习,获得
W
W
W和
b
b
b。
感知器算法(Perceptron Algorithm):
(1)随机选择
W
W
W和
b
b
b;
(2)取一个训练样本
(
X
,
y
)
(X, y)
(X,y)
(i) 若
W
T
X
+
b
>
0
W^T X + b > 0
WTX+b>0且
y
=
−
1
y = -1
y=−1,则:
W
=
W
−
X
,
b
=
b
−
1.
W = W - X, b = b - 1.
W=W−X,b=b−1.
(ii)若
W
T
X
+
b
<
0
W^T X + b < 0
WTX+b<0且
y
=
+
1
y = +1
y=+1,则:
W
=
W
+
X
,
b
=
b
+
1.
W = W + X, b = b + 1.
W=W+X,b=b+1.
(3)再取另一个
(
X
,
y
)
(X, y)
(X,y),回到(2);
(4)终止条件:直到所有输入输出对
(
X
,
y
)
(X, y)
(X,y)都不满足(2)中(i)和(ii)之一,退出循环。
感知器算法演示:
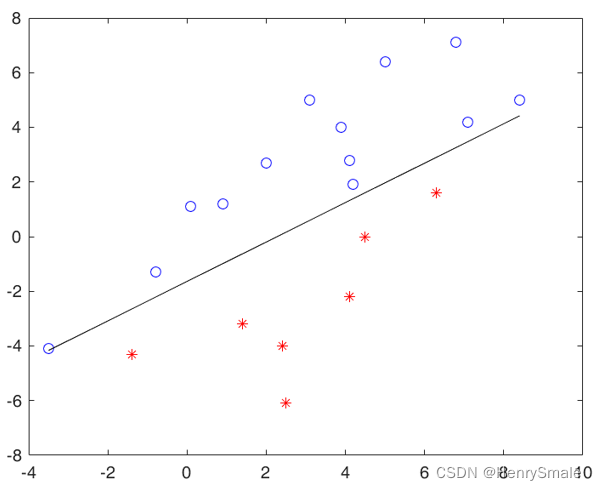
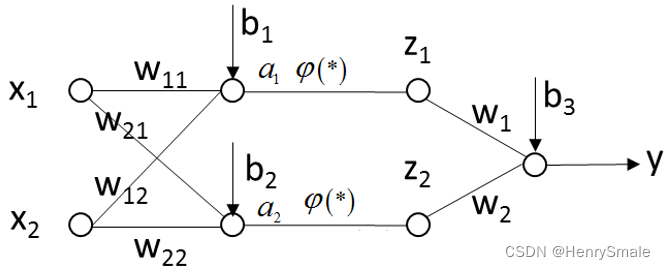
1.4 多层网络
两层神经网络例子: