问题提出

在做一道题的时候有这样一步：两边平方，最后求解，题很简单，但是这个方法是否能这么用引起了我的好奇。

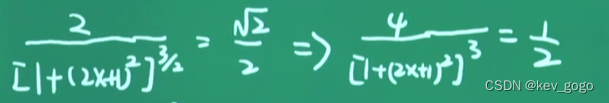
思考

首先不妨假设一个通用的方程：
$$f(x)=g(x)$$
然后我们对方程两边平方：
$$f^2(x)=g^2(x)$$
再通过移项可得：
$$f^2(x)-g^2(x)=0$$
最后可以写成：
$$(f(x)-g(x))(f(x)+g(x))=0$$
可以发现，除了最开始的解，还增加了一个下式的解：
$$f(x)+g(x)=0$$

总结

对方程两边进行平方可能会增根。