1. 算法介绍

算法目的：求图中某点 s 到其余各点的最短距离
算法步骤：

初始化距离数组 dis 和优先级队列，其中 dis[i] 表示 s 点到当前 i 点的最短距离，优先级队列储存的是已经求出最短距离的点，按与 s 点之间的距离从小到大排序；
每次取出距离 s 最近的一个点 c，遍历 c 所能到达的相邻点 n，尝试更新 s 点到 n 的距离（如果 dis[c] + c 到 n 之间的距离 < dis[n], 就更新 dis[n] = dis[c] + c 到 n 之间的距离），并将 n 加入优先级队列；
重复第二步，直至队列为空。

2. 实战

2.1 Reachable Nodes In Subdivided Graph

Leetcode: 882. Reachable Nodes In Subdivided Graph

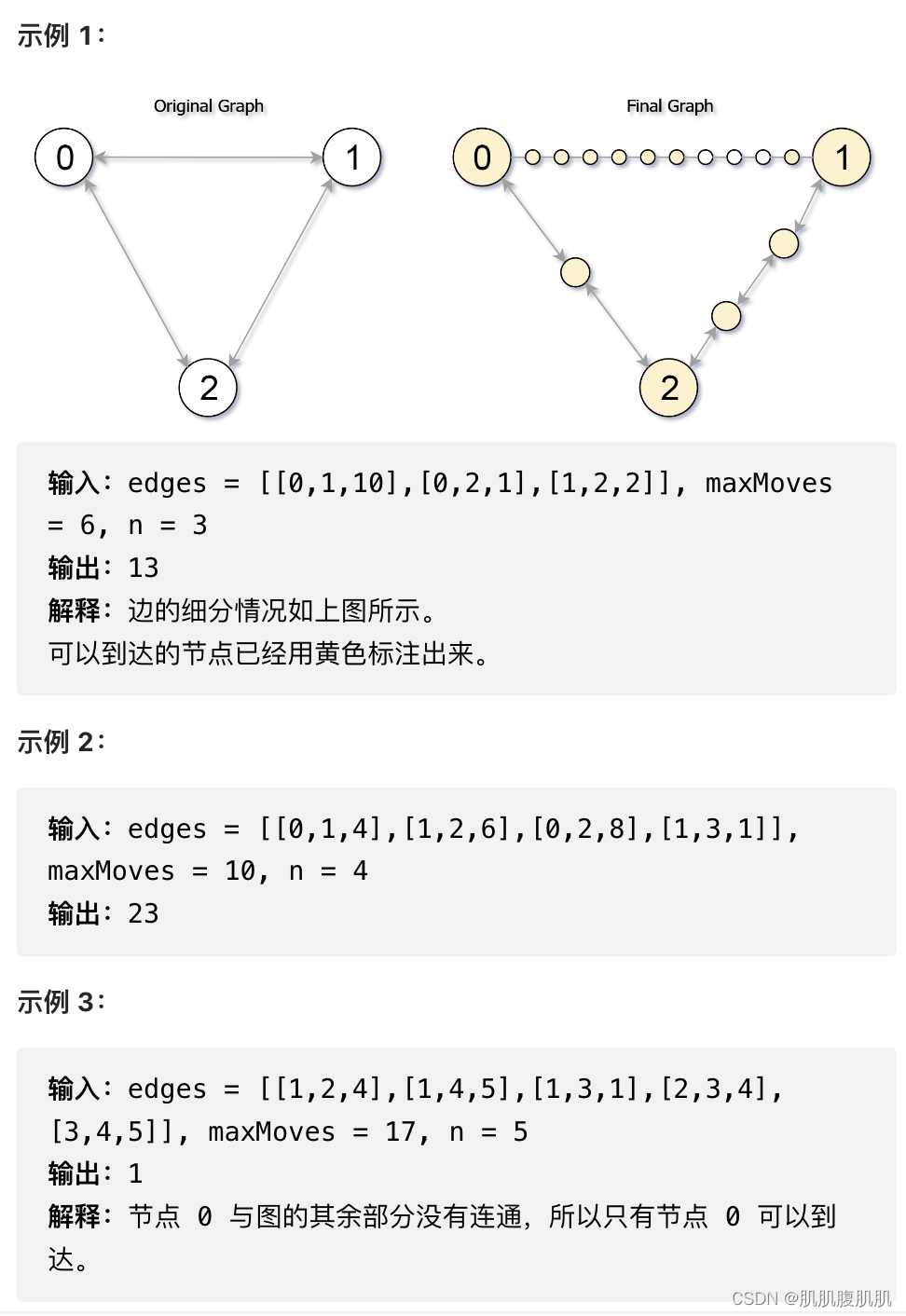
题目描述：给你一个无向图（原始图），图中有 n 个节点，编号从 0 到 n - 1 。你决定将图中的每条边细分为一条节点链，每条边之间的新节点数各不相同。
图用由边组成的二维数组 edges 表示，其中 edges[i] = [ui, vi, cnti] 表示原始图中节点 ui 和 vi 之间存在一条边，cnti 是将边细分后的新节点总数。注意，cnti == 0 表示边不可细分。
要细分边 [ui, vi] ，需要将其替换为 (cnti + 1) 条新边，和 cnti 个新节点。新节点为 x1, x2, …, xcnti ，新边为 [ui, x1], [x1, x2], [x2, x3], …, [xcnti+1, xcnti], [xcnti, vi] 。
现在得到一个新的细分图，请你计算从节点 0 出发，可以到达多少个节点？如果节点间距离是 maxMoves 或更少，则视为可以到达。
给你原始图和 maxMoves ，返回新的细分图中从节点 0 出发可到达的节点数。
在这里插入图片描述

代码：

class Solution {
    public int reachableNodes(int[][] edges, int maxMoves, int n) {
        List<int[]>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int[] pair : edges) {
            int from = pair[0], to = pair[1], edge = pair[2] + 1;
            g[from].add(new int[]{to, edge});
            g[to].add(new int[]{from, edge});
        }

        PriorityQueue<int[]> pq = new PriorityQueue<>((e1, e2) -> e1[1] - e2[1]);
        pq.offer(new int[]{0, 0});
        int[] dis = new int[n];
        Arrays.fill(dis, maxMoves + 1);
        dis[0] = 0;
        boolean[] visited = new boolean[n];
        while (!pq.isEmpty()) {
            int curr[] = pq.poll();
            int currNode = curr[0];
            if (visited[currNode]) continue;
            visited[currNode] = true;
            for (int[] next : g[currNode]) {
                int nextNode = next[0], nextDis = next[1];
                if (!visited[nextNode] && dis[currNode] + nextDis < dis[nextNode]) {
                    dis[nextNode] = dis[currNode] + nextDis;
                    pq.offer(new int[]{nextNode, dis[nextNode]});
                }
            }
        }
        int ans = 0;


        for (int i = 0; i < n; i++) {
            if (dis[i] <= maxMoves) {
                ans++;
            }
        }

        for (int[] pair : edges) {
            ans += Math.min(pair[2], Math.max(0, maxMoves - dis[pair[0]]) + Math.max(0, maxMoves - dis[pair[1]]));
        }

        return ans;

    }
}