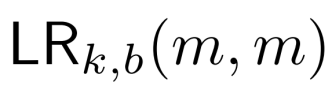细分图中的可到达节点 : 常规最短路运用题

news2025/2/27 8:15:17

题目描述

Tag : 「最短路」、「单源最短路」、「Dijkstra」、「SPFA」

给你一个无向图（原始图），图中有 n 个节点，编号从 0 到 n - 1 。你决定将图中的每条边细分为一条节点链，每条边之间的新节点数各不相同。

图用由边组成的二维数组 edges 表示，其中 edges[i] = [u_{i}, v_{i}, cnt_{i}]edges[i]=[ui,vi,cnti] 表示原始图中节点 u_{i}ui 和 v_{i}vi 之间存在一条边，cnt_{i}cnti 是将边细分后的新节点总数。注意，cnt_{i} = 0cnti=0 表示边不可细分。

要细分边 [u_{i}, v_{i}][ui,vi] ，需要将其替换为 (cnt_{i} + 1)(cnti+1) 条新边，和 cnt_{i}cnti 个新节点。新节点为 x_1, x_2, ..., x_{cnt_{i}}x1,x2,...,xcnti ，新边为 [u_{i}, x_{1}], [x_{1}, x_{2}], [x_{2}, x_{3}], ..., [x_{cnt_{i}}+1, x_{cnt_{i}}], [x_{cnt_{i}}, v_{i}][ui,x1],[x1,x2],[x2,x3],...,[xcnti+1,xcnti],[xcnti,vi] 。

现在得到一个新的细分图，请你计算从节点 0 出发，可以到达多少个节点？如果节点间距离是 maxMoves 或更少，则视为可以到达。

给你原始图和 maxMoves ，返回新的细分图中从节点 0 出发可到达的节点数。

示例 1：

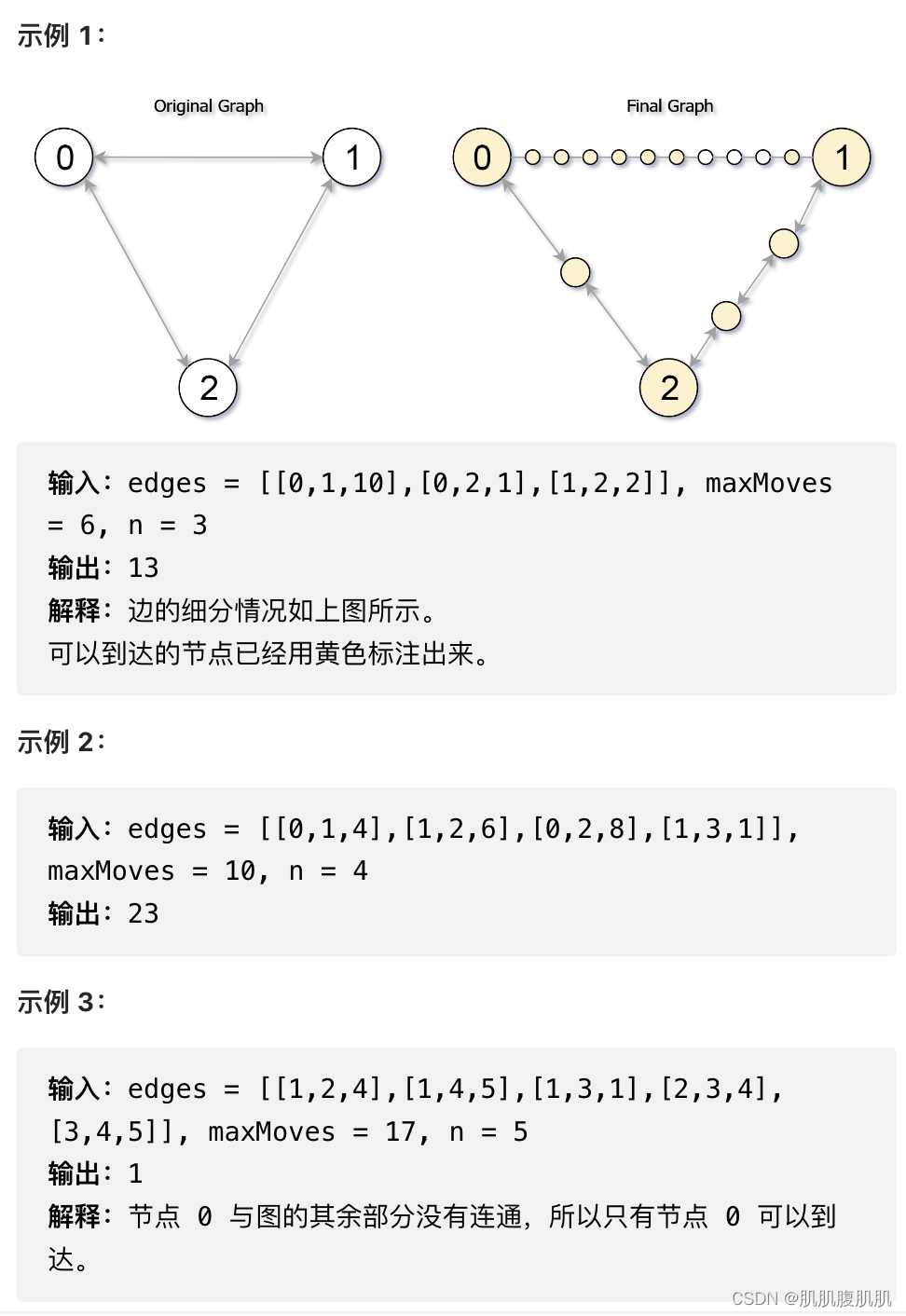
输入：edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3

输出：13

解释：边的细分情况如上图所示。
可以到达的节点已经用黄色标注出来。
复制代码

示例 2：

输入：edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4

输出：23
复制代码

示例 3：

输入：edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5

输出：1

解释：节点 0 与图的其余部分没有连通，所以只有节点 0 可以到达。
复制代码

提示：

0 <= edges.length <= \min(n * (n - 1) / 2, 10^4)0<=edges.length<=min(n∗(n−1)/2,104)
edges[i].length = 3edges[i].length=3
0 <= u_{i} < v_{i} < n0<=ui<vi<n
图中不存在平行边
0 <= cnt_{i} <= 10^40<=cnti<=104
0 <= maxMoves <= 10^90<=maxMoves<=109
1 <= n <= 30001<=n<=3000

朴素 Dijkstra

为了方便，我们将原始图边的数量记为 m，因此对于原始图而言，点的数量 30003000，边的数量为 1000010000。

题目要我们求新图上，从 0 点出发可到达的点的数量，我们将原图上存在的点称为「原点」，细分边上增加的点称为「细分点」，两类点中可达点的数量即是答案。

在分别考虑如何统计两类点之前，我们需要重新定义一下边的权重：若原点 u 和原点 v 的边上存在 c 个细分点，我们将原点 u 和原点 v 之间的边看作是一条权重为 c + 1 的无向边（结合题意，c 个点存在 c + 1 个分段/距离）。

重新定义边的权重后，因为该图是「稠密图」，我们可以使用「朴素 Dijkstra」来求解最短路，得到 distdist 数组，其中 dist[x] = tdist[x]=t 含义为从原点 0 点出发，到达原点 x 的最短距离为 t。

不了解最短路的同学可以看前置 🧀 : 涵盖所有的「存图方式」与「最短路算法（详尽注释）」

随后考虑如何统计答案（可达点的数量），根据统计点的类型分情况讨论：

对于原点：若有 dist[x] < maxdist[x]<max 的话，说明原点 x 可达，累加到答案中；
对于细分点：由于所有的细分点都在原图边上，因此我们可以统计所有原图边上有多少细分点可达。对于任意一条边 e(u, v)e(u,v) 而言，该边上可达点数量包含「经过原点 u 可达」以及「经过原点 v 可达」的交集，其中原点 0 到达原点 u 以及原点 v 的距离，我们是已知的。因此经过原点 u 可达的数量为 \max(0, max - dist[u])max(0,max−dist[u])，经过原点 v 可达的数量为 \max(0, max - dist[v])max(0,max−dist[v])，两者之和与该边上细分点的总数取 min 即是这条边可达点的数量。

代码：

class Solution {
    static int N = 3010, INF = 0x3f3f3f3f;
    static int[][] g = new int[N][N];
    static int[] dist = new int[N];
    static boolean[] vis = new boolean[N];
    public int reachableNodes(int[][] edges, int max, int n) {
        // 建图
        for (int i = 0; i < n; i++) Arrays.fill(g[i], INF);
        for (int[] info : edges) {
            int a = info[0], b = info[1], c = info[2] + 1;
            g[a][b] = g[b][a] = c;
        }
        // 朴素 Dijkstra
        Arrays.fill(dist, INF);
        Arrays.fill(vis, false);
        dist[0] = 0;
        for (int i = 0; i < n; i++) {
            int t = -1;
            for (int j = 0; j < n; j++) {
                if (!vis[j] && (t == -1 || dist[j] < dist[t])) t = j;
            }
            vis[t] = true;
            for (int j = 0; j < n; j++) dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
        }
        // 统计答案
        int ans = 0;
        for (int i = 0; i < n; i++) {
            if (dist[i] <= max) ans++;
        }
        for (int[] info : edges) {
            int a = info[0], b = info[1], c = info[2];
            int c1 = Math.max(0, max - dist[a]), c2 = Math.max(0, max - dist[b]);
            ans += Math.min(c, c1 + c2);
        }
        return ans;
    }
}
复制代码

时间复杂度：建图复杂度为 O(m)O(m)；使用朴素 Dijkstra 求最短路复杂度为 O(n^2)O(n2)；统计答案复杂度为 O(n + m)O(n+m)。整体复杂度为 O(m + n^2)O(m+n2)
空间复杂度：O(n^2)O(n2)

SPFA

从数据范围来看，无论是朴素 Dijkstra 还是堆优化版的 Dijkstra 都可以过，复杂度分别为 O(n^2)O(n2) 和 O(m\log{n})O(mlogn)。

那 Bellman Ford 类的单源最短路就无法通过了吗？

理论上，无论是 Bellman Ford 还是 SPFA 复杂度均为 O(n \times m)O(n×m)，均无法通过本题。但实际上 SPFA 由于使用队列对松弛顺序进行了调整，因此在应对「非菊花图」时均表现良好，复杂度可视为 O(k \times m)O(k×m)，近似 O(m)O(m)。

代码：

class Solution {
    static int N = 3010, M = 20010, INF = 0x3f3f3f3f, idx = 0;
    static int[] he = new int[N], e = new int[M], ne = new int[M], w = new int[M];
    static int[] dist = new int[N];
    static boolean[] vis = new boolean[N];
    void add(int a, int b, int c) {
        e[idx] = b;
        ne[idx] = he[a];
        w[idx] = c;
        he[a] = idx++;
    }
    public int reachableNodes(int[][] edges, int max, int n) {
        // 建图
        Arrays.fill(he, -1);
        idx = 0;
        for (int[] info : edges) {
            int a = info[0], b = info[1], c = info[2] + 1;
            add(a, b, c); add(b, a, c);
        }
        // SPFA
        Arrays.fill(dist, INF);
        Arrays.fill(vis, false);
        Deque<Integer> d = new ArrayDeque<>();
        d.addLast(0);
        dist[0] = 0;
        vis[0] = true;
        while (!d.isEmpty()) {
            int t = d.pollFirst();
            vis[t] = false;
            for (int i = he[t]; i != -1; i = ne[i]) {
                int j = e[i];
                if (dist[j] > dist[t] + w[i]) {
                    dist[j] = dist[t] + w[i];
                    if (vis[j]) continue;
                    d.addLast(j);
                    vis[j] = true;
                }
            }
        }
        // 统计答案
        int ans = 0;
        for (int i = 0; i < n; i++) {
            if (dist[i] <= max) ans++;
        }
        for (int[] info : edges) {
            int a = info[0], b = info[1], c = info[2];
            int c1 = Math.max(0, max - dist[a]), c2 = Math.max(0, max - dist[b]);
            ans += Math.min(c, c1 + c2);
        }
        return ans;
    }
}
复制代码