一、前言

本文主要讲了 Bellman-ford 和 SPFA 算法概念和相应例题。

二、Bellman-ford算法

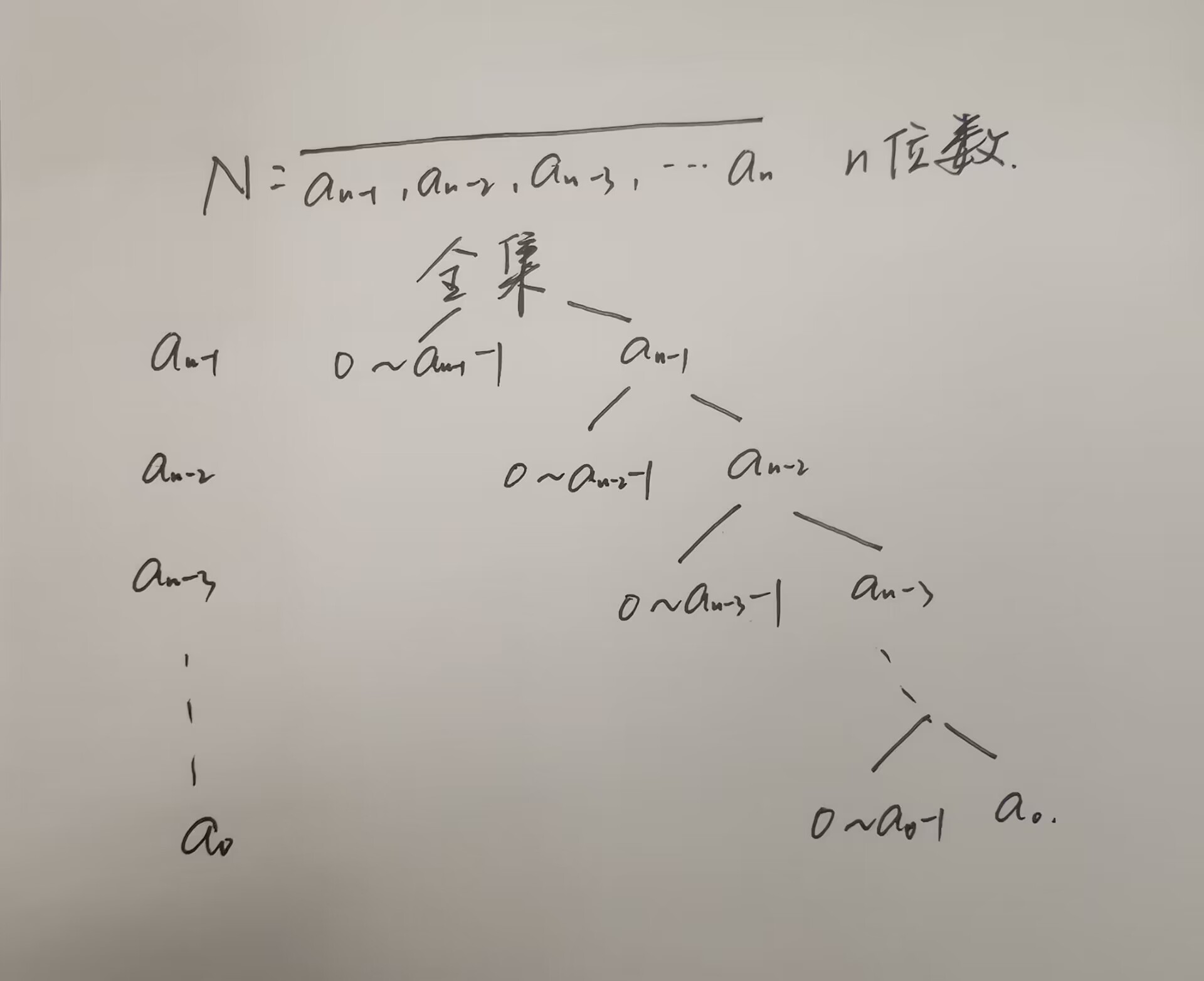
单源最短路径问题：给定一个起点 s，求它到图中所有 n 个结点的最短路径。

1、算法思想

图中每个点上站着一个 “警察”。
每个警察问邻居：走你这条路能到 s 吗？有多远？
反复问多次，最后所有警察都能得到最短路。

第1轮，给所有 n 个人每人一次机会，问他的邻居，到 s 的最短距离是多少？更新每人到 s 的最短距离。特别地，在 s 的直连邻居中，有个 t，得到了到 s 的最短距离。(注意，算法并没有查找是哪个 t）
第2轮，重复第 1 轮的操作。

更新每人到 s 的最短距离。

特别地，在 s 和 t 的直连邻居中，有个 v，得到了到 s 的最短距离。

第3轮，……

2、算法复杂度

一共需要几轮操作？每一轮操作，都至少有一个新的结点得到了到 s 的最短路径。所以，最多只需要 n 轮操作，就能完成 n 个结点。
在每一轮操作中，需要检查所有 m 个边，更新最短距离。
Bellman-Ford算法的复杂度： O(nm)。

3、判断负圈

Bellman-Ford 能判断负圈。
没有负圈时，只需要n轮就结束。
如果超过n轮，最短路径还有变化，那么肯定有负圈。

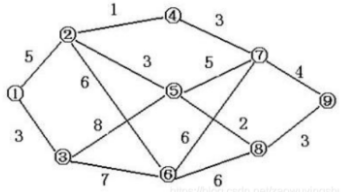
4、出差（2022第十三届国赛，lanqiaoOJ题号2194）

【题目描述】

A国有 N 个城市，编号为 1...N，小明是编号为 1 的城市中一家公司的员工，需要去编号为 N 的城市出差。由于疫情原因，小明无法乘坐飞机直接从城市 1 到达城市 N，需要通过其他城市进行陆路交通中转。小明通过交通信息网，查询到了 M 条城市之间仍然还开通的路线信息以及每一条路线需要花费的时间。由于疫情原因，小明到达一个城市后需要隔离观察一段时间才能离开该城市前往其他城市。通过网络，小明也查询到了各个城市的隔离信息。(小明之前在城市 1，可以直接离开城市 1，不需要隔离）小明希望能够尽快赶到城市 N，你帮他规划一条路线，能够在最短时间内到达城市 N。

【输入】

第1行：两个正整数 N, M，N 表示 A 国的城市数量，M 表示未关闭的路线数量。第2行：N 个正整数，第 i 个整数 Ci 表示到达编号为 i 的城市后需要隔离的时间。第 3 ... M+2 行：每行 3 个正整数， u, v, c 表示有一条城市 u 到城市 v 的双向路线仍然开通着，通过该路线的时间为 c。

【输出】

第1行：1 个正整数，表示小明从城市 1 出发到达城市 N 的最短时间 (到达城市 N，不需要计算城市 N 的隔离时间）。

对于 100% 的数据，1≤N≤1000，1≤M≤10000，1≤Ci≤200, 1≤u, v≤N, 1≤c≤1000

【样例输入】

4 4

5 7 3 4

1 2 4

1 3 5

2 4 3

3 4 5

【样例输出】

13

思考：

本题求最短路径，数据规模 1≤N≤1000, 1≤M≤10000 不算大。
用什么算法？本题是单源最短路径问题。用复杂度 O(n^3) 的多源最短路算法 floyd 算法超时；用复杂度 O(mn) 的单源最短路 Bellman-ford 算法正好；
没有必要使用更好的 Dijkstra 和 SPFA 算法。两点之间的边长，除了路线时间 c，还要加上隔离时间。经过这个转化后，本题是一道简单的 Bellman-ford 算法模板题。

n,m=map(int,input().split())   #n:城市。m:路线
c=[0]+[int(i) for i in input().split()]   #隔离时间
#G=[[0]*(n+1) for i in range(n+1)]
e=[]                            #存每一条边
for i in range(m):
    u,v,w=map(int,input().split())
    e.append((u,v,w))
    e.append((v,u,w))       #双向边，没有的话会报错
INF=1<<64
dis=[INF]*(n+1)
dis[1]=0
for k in range(1,n+1):  #n个点，执行n轮问路
    for u,v,w in e:
        res=c[v]
        if v==n:
            res=0
        dis[v]=min(dis[v],dis[u]+w+res)
print(dis[n])

可惜该题解还是会部分超时。

三、SPFA算法：改进的Bellman-Ford

SPFA=队列处理+ Bellman-Ford。
Bellman-Ford算法有很多低效或无效的操作。其核心内容，是在每一轮操作中，更新所有结点到起点s的最短距离。
计算和调整一个结点u到s的最短距离后，如果紧接着调整u的邻居结点，这些邻居肯定有新的计算结果；而如果漫无目的地计算不与u相邻的结点，很可能毫无变化，所以这些操作是低效的。
改进：计算结点u之后，下一步只计算和调整它的邻居，能减少计算。
这些步骤用队列进行操作，这就是SPFA。

SPFA步骤：

1）起点 s 入队，计算它所有邻居到 s 的最短距离。把 s 出队，状态有更新的邻居入队，没更新的不入队。

2）现在队列的头部是 s 的一个邻居 u。弹出 u，更新它所有邻居的状态，把其中有状态变化的邻居入队列。

3）继续以上过程，直到队列空。这也意味着，所有结点的状态都不再更新。最后的状态就是到起点 s 的最短路径。

SPFA不稳定：

弹出 u 之后，在后面的计算中，u 可能会再次更新状态 (后来发现，u 借道别的结点去 s，路更近)。所以，u 可能需要重新入队列。
有可能只有很少结点重新进入队列，也有可能很多。这取决于图的特征。
所以，SPFA 是不稳定的。

1、随机数据下的最短路问题（lanqiaoOJ题号1366）

【题目描述】

给定 N 个点和 M 条单向道路，每条道路都连接着两个点，每个点都有自己编号，分别为 1~ N。问你从 S 点出发，到达每个点的最短路径为多少。

【输入描述】

输入第一行包含三个正整数 N, M, S。第 2 到 M+1 行每行包含三个正整数 u, v, w，表示 u→v 之间存在一条距离为 w 的路。1≤N≤5×10^3，1≤M≤5×10^4，1≤ui, vi≤N，0≤wi≤10^9

【输出描述】

输出仅一行，共 N 个数，分别表示从编号 S 到编号为 1~ N 点的最短距离，两两之间用空格隔开。(如果无法到达则输出-1)

import heapq
def spfa(s):
    dis[s]=0
    hp=[]
    heapq.heappush(hp,s)    #用heapq处理优先队列
    inq=[0]*(n+1)   #标志某一点是否已访问
    inq[s]=1      
    while hp:
        u=heapq.heappop(hp)
        inq[u]=0
        if dis[u]==INF:
            continue
        for v,w in e[u]:    #遍历点u的邻居v,边长为w
            if dis[v]>dis[u]+w:
                dis[v]=dis[u]+w
                if inq[v]==0:
                    heapq.heappush(hp,v)
                    inq[v]=1

n,m,s=map(int,input().split())
e=[[] for i in range(n+1)]
INF=1<<64
dis=[INF]*(n+1)
for _ in range(m):
    u,v,w=map(int,input().split())
    e[u].append((v,w))          #u的邻居是v，边长是w
spfa(s)
for i in range(1,n+1):
    if dis[i]>=INF:
        print("-1",end=' ')
    else:
        print(dis[i],end=' ')

另外，spfa也能判断负环。

Neq[i]：表示一个任意点 i 进队列的次数，如果大于 n 次，就出现了负环。

补充：

【SPFA的简单优化】

SPFA 算法的主要操作是把变化的点放进队列。这些点差不多是随机放进队列的，如果改变进队和出队的顺序，是否能加快所有点的最短路计算？下面是两个小优化。

1）进队的优化：SLF (Small Label First)

需要使用双端队列 deque。

队头出队后，需要把它的有变化的邻居放进队列。把进队的点 u 与新队头 v 进行比较，如果 dis[u] < dis[v]，将 u 其插入到队头，否则插入到队尾。这个优化使得队列弹出的队头都是路径较短的点，从而加快所有点的最短路的计算。

2）出队的优化：LLL (Large Label Last)

计算队列中所有点的 dis 的平均值 x，每次选一个小于 x 的点出队。具体操作是：如果队头 u 的dis[u] > x，把 u 弹出然后放到队尾去，然后继续检查新的队头 v，直到找到一个 dis[v]<x 为止。这个优化也是先处理了更短的点。

【比较 Bellman-ford 算法和 Dijkstra 算法】

Dijkstra 算法是一种 “集中式” 算法，Bellman-ford 算法是一种“分布式”算法。图上有 n 个点，假设每个点上都有一台独立的计算机，现在让每个点计算它到其他所有点的最短路，两种算法的特点分别是：

1）Dijkstra 算法。计算一个起点 s 到其他所有点的最短路，是以 s 为中心点扩散出去，对其他所有点进行的计算都是围绕着起点 s 的，复杂度 O(m×logn)。每个点上的计算机独自做自己的计算，不管其他点的计算结果。Dijkstra 算法是一种 “集中式” 算法，点与点之间 “独立计算，互不干涉”。

2）Bellman-ford 算法。对任意一个点来说，它需要做的只是逐个询问它的所有邻居：有没有到其他点的更短的路？如果有则更新，并把这个更新告诉它的其他邻居，以方便这些邻居也做更新。经过 n 轮询问，就得到了它到其他所有点的最短路。设一个点平均有 10 个邻居，那么这个点上的计算机只需做 10×n 次计算，就能确定它到图中其他所有点的最短路。Bellman-ford 算法是一种 “分布式” 计算，点与点之间通过互相交换信息来计算最短路径，可以概况为 “合作计算，互通有无”。

Bellman-ford 的复杂度是 O(m×n)，比 Dijkstra 的 O(m×logn) 差，这是在单机上。如果是并行计算，每个点单独计算，Bellman-ford 比 Dijkstra 算法的效率更高，计算也更简单。

以上，Bellman-ford和SPFA算法

祝好