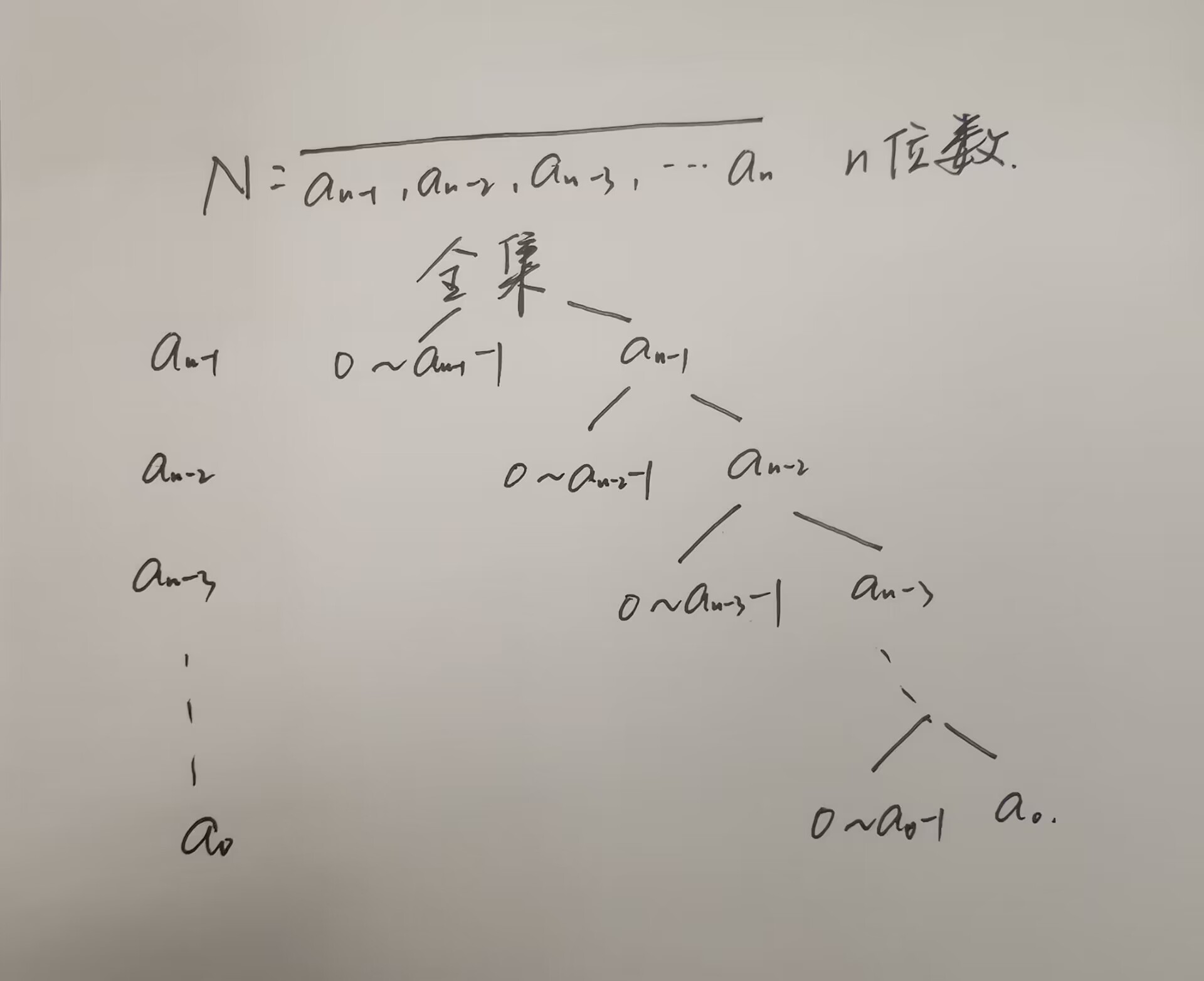
数位dp的题目一般会问,某个区间内,满足某种性质的数的个数。
- 利用前缀和,比如求区间[l,r]中的个数,转化成求[0,r]的个数 [0,l-1]的个数。
- 利用树的结构来考虑(按位分类讨论)
1081. 度的数量
#include<bits/stdc++.h>
using namespace std;
const int N=35;
int f[N][N],l,r,K,B;
//预处理组合数
int init()
{
for(int i=0;i<N;i++)
for(int j=0;j<=i;j++)
if(!j) f[i][j]=1;
else f[i][j]=f[i-1][j]+f[i-1][j-1];
}
int dp(int n)
{
if(!n) return 0;
vector<int>vec;
while(n) vec.push_back(n%B),n/=B;//十进制转成B进制
int res=0,last=0;
//res记录答案数,last表示用了多少个1
for(int i=vec.size()-1;i>=0;i--)
{
int x=vec[i];//取出第i位数
if(x)//(如果当前位x==0直接进入右分支,讨论下一位)
{
res+=f[i][K-last];
//当前位填0,从剩下的所有位(共有i位)中选K-last个数。
//对应于:左分支中0的情况,合法
if(x>1)
{
res+=f[i][K-last-1];
break;
}
else//x==1,直接讨论下一位,可用的1的个数减1
{
last++;
if(last>K) break;
}
}
if(i==0&&last==K) res++;//遍历到最后一位且最后一位取1
}
return res;
}
int main()
{
init();
cin>>l>>r>>K>>B;
cout<<dp(r)-dp(l-1)<<endl;
return 0;
}
1082. 数字游戏
#include<bits/stdc++.h>
using namespace std;
const int N=15;
int f[N][N],l,r;
//f[i][j]表示一共有i位,且最高位为j的数的个数
int init()
{
for(int j=0;j<=9;j++) f[1][j]=1;
for(int i=2;i<N;i++)
for(int j=0;j<=9;j++)
for(int k=j;k<=9;k++)
f[i][j]+=f[i-1][k];
}
int dp(int n)
{
if(!n) return 1;
vector<int>vec;
while(n) vec.push_back(n%10),n/=10;
int res=0,last=0;
//res记录答案数,last表示上一位的数字
for(int i=vec.size()-1;i>=0;i--)
{
int x=vec[i];//取出第i位数
if(last>x) break;//这一位数无论怎么取都比上一位小
for(int j=last;j<vec[i];j++)//进入左分支讨论
res+=f[i+1][j];
last=x;//更新lat
if(!i) res++;//到了最后一位,剩下一种合法的情况
}
return res;
}
int main()
{
init();
while(cin>>l>>r)
cout<<dp(r)-dp(l-1)<<endl;
return 0;
}
1083. Windy数
#include<bits/stdc++.h>
using namespace std;
const int N=11;
int f[N][N],l,r;
//f[i][j]表示一共有i位,且最高位为j的数的个数
//存的是(包含前导零)的情况
int init()
{
for(int j=0;j<=9;j++) f[1][j]=1;
for(int i=2;i<N;i++)
for(int j=0;j<=9;j++)
for(int k=0;k<=9;k++)
if(abs(j-k)>=2) f[i][j]+=f[i-1][k];
}
int dp(int n)
{
if(!n) return 0;
vector<int>vec;
while(n) vec.push_back(n%10),n/=10;
int res=0,last=-2;
//res记录答案数,last表示上一位的数字
for(int i=vec.size()-1;i>=0;i--)
{
int x=vec[i];//取出第i位数
for(int j=(i==vec.size()-1);j<x;j++)//首位不能取到零,其他位可以
if(abs(j-last)>=2) res+=f[i+1][j];
if(abs(x-last)>=2) last=x;
else break;
if(!i) res++;
}
for(int i=1;i<vec.size();i++)
for(int j=1;j<=9;j++)
res+=f[i][j];//特判首位为零的情况
return res;
}
int main()
{
init();
cin>>l>>r;
cout<<dp(r)-dp(l-1)<<endl;
return 0;
}
1084. 数字游戏 II
f[i][j][k] 表示一共有i位,且最高位数字是j,且所有位数字和%P结果为k的数的个数,若要转移到f[i][j][k]的状态,在i-1位对于每个x(x取值0~9)都应使第三维为(k-j)%P
状态转移方程:
f
[
i
]
[
j
]
[
k
]
=
∑
k
=
0
P
−
1
∑
x
=
0
9
f
[
i
−
1
]
[
x
]
[
(
k
−
j
)
%
P
]
f[i][j][k]=\sum_{k=0}^{P-1}\sum_{x=0}^{9}f[i-1][x][(k-j)\%P]
f[i][j][k]=∑k=0P−1∑x=09f[i−1][x][(k−j)%P]
用last表示到当前为止,前面数位上的数字之和,对此,当前第i位数字为j,前面数字之和为last,那么
后i位(包括j这一位)数字之和sum与last的关系就是
(last+sum)%N==0,那么sum%N==(-last)%N,
所以res+=f[i+1][j][(-last%N)];
#include<bits/stdc++.h>
using namespace std;
const int N=11;
int f[N][N][110],l,r,P;
//f[i][j][k]表示一共有i位,且最高位数字是j,且所有位数字和%P结果为k的数的个数
int mod(int u,int v)
{
return (u%v+v)%v;
}
int init()
{
memset(f,0,sizeof f);
for(int i=0;i<=9;i++) f[1][i][i%P]++;
for(int i=2;i<N;i++)
for(int j=0;j<=9;j++)
for(int k=0;k<P;k++)
for(int x=0;x<=9;x++)
f[i][j][k]+=f[i-1][x][mod(k-j,P)];
}
int dp(int n)
{
if(!n) return 1;
vector<int>vec;
while(n) vec.push_back(n%10),n/=10;
int res=0,last=0;
//res记录答案数,last表示前面所有位数上数字的和
for(int i=vec.size()-1;i>=0;i--)
{
int x=vec[i];
for(int j=0;j<x;j++) //第i位放0~x-1
res+=f[i+1][j][mod(-last,P)]; //0~i位,所以一共有i+1位
last+=x;
if(!i&&last%P==0) res++;
}
return res;
}
int main()
{
while(cin>>l>>r>>P)
{
init();
cout<<dp(r)-dp(l-1)<<endl;
}
return 0;
}
1085. 不要62
#include<bits/stdc++.h>
using namespace std;
const int N=11;
int f[N][N],l,r;
//f[i][j]表示一共有i位,且最高位为j的数的个数
int init()
{
for(int j=0;j<=9;j++)
if(j!=4) f[1][j]=1;//一位不含5
for(int i=2;i<N;i++)
for(int j=0;j<=9;j++)
{
if(j==4) continue;
for(int k=0;k<=9;k++)
{
if(k==4||(j==6&&k==2)) continue;
f[i][j]+=f[i-1][k];
}
}
}
int dp(int n)
{
if(!n) return 1;
vector<int>vec;
while(n) vec.push_back(n%10),n/=10;
int res=0,last=0;
//res记录答案数,last表示上一位的数字
for(int i=vec.size()-1;i>=0;i--)
{
int x=vec[i];//取出第i位数
for(int j=0;j<x;j++)
{
if(j==4||(j==2&&last==6)) continue;
res+=f[i+1][j];
}
if(x==4||(x==2&&last==6)) break;
last=x;
if(!i) res++;
}
return res;
}
int main()
{
init();
while(cin>>l>>r,l||r)
cout<<dp(r)-dp(l-1)<<endl;
return 0;
}