5.1 子空间
5.1.1. 定义
设 W ⊂ C n W\subset C^n W⊂Cn ,即子空间对线性组合封闭
若 ( 1 ) 对 ∀ α , β ∈ W , 有 α + β ∈ W ( 对 加 法 封 闭 ) ( 2 ) 对 ∀ α ∈ W , ∀ k ∈ C , 有 k α ∈ W ( 对 数 乘 封 闭 ) \begin{aligned} 若 &(1)对\forall \alpha,\beta\in W,有\alpha+\beta\in W(对加法封闭)\\ &(2)对\forall \alpha\in W,\forall k\in C ,有k\alpha \in W(对数乘封闭) \end{aligned} 若(1)对∀α,β∈W,有α+β∈W(对加法封闭)(2)对∀α∈W,∀k∈C,有kα∈W(对数乘封闭)
-
子空间 W 一定含有零向量 0 ⃗ ∈ W \vec{0} \in W 0∈W;若不包含零向量,则不是子空间
-
齐次方程解集 W ( A ) = { X ∈ C n ∣ A X = 0 } W(A)=\{X\in C^n\vert AX=0\} W(A)={X∈Cn∣AX=0} ,对加法,数乘封闭( A X 1 = 0 , A X 2 = 0 , A ( X 1 + X 2 ) = 0 AX_1=0,AX_2=0,A(X_1+X_2)=0 AX1=0,AX2=0,A(X1+X2)=0),( A X 1 = 0 AX_1 =0 AX1=0, A ( k X 1 ) = k ( A X 1 ) = 0 A(kX_1)=k(AX_1)=0 A(kX1)=k(AX1)=0) ,且有零向量
-
非齐次方程解集 W ( A ) = { X ∈ C n ∣ A X = b ≠ 0 } W(A)=\{X\in C^n\vert AX=b\neq 0\} W(A)={X∈Cn∣AX=b=0} 不含零向量,故W(A) 不是子空间,且对加法,数乘不封闭
5.1.2 生成子空间
a. 引理
由 C n C^n Cn 中向量 α 1 , α 2 ⋯ , α m \alpha_1,\alpha_2\cdots,\alpha_m α1,α2⋯,αm 的所有线性组合生成的向量集合 W ( A ) = { x = k 1 α 1 + k 2 α 2 + ⋯ + k m α m } W(A)=\{x=k_1\alpha_1+k_2\alpha_2+\cdots+k_m\alpha_m\} W(A)={x=k1α1+k2α2+⋯+kmαm} 是一个子空间,称W为由 α 1 , ⋯ , α m \alpha_1,\cdots,\alpha_m α1,⋯,αm 生成的子空间,记为 W = L ( α 1 , ⋯ , α m ) W=L(\alpha_1,\cdots,\alpha_m) W=L(α1,⋯,αm) 或 W = s p a n ( α 1 , ⋯ , α m ) W=span(\alpha_1,\cdots,\alpha_m) W=span(α1,⋯,αm)
5.1.3 基定义
若 ( 1 ) 子 空 间 W 中 有 r 个 向 量 α 1 , ⋯ , α r 线 性 无 关 ( 2 ) W 中 任 一 向 量 α 可 由 α 1 , ⋯ , α r 表 示 : α = k 1 α 1 + ⋯ + k r α r 则 称 [ α 1 , ⋯ , α r ] 为 W 的 一 个 基 , r 为 W 的 维 数 , 记 作 d i m W = r \begin{aligned} 若 &(1)子空间W中有r个向量\alpha_1,\cdots,\alpha_r线性无关\\ &(2)W中任一向量\alpha可由\alpha_1,\cdots,\alpha_r表示:\alpha=k_1\alpha_1+\cdots+k_r\alpha_r\\ 则&称[\alpha_1,\cdots,\alpha_r]为W的一个基,r为W的维数,记作dim W=r \end{aligned} 若则(1)子空间W中有r个向量α1,⋯,αr线性无关(2)W中任一向量α可由α1,⋯,αr表示:α=k1α1+⋯+krαr称[α1,⋯,αr]为W的一个基,r为W的维数,记作dimW=r
空间W可由基 α 1 , ⋯ , α r \alpha_1,\cdots,\alpha_r α1,⋯,αr 生成,即 W = L ( α 1 , ⋯ , α r ) W=L(\alpha_1,\cdots,\alpha_r) W=L(α1,⋯,αr) 或 W = s p a n ( α 1 , ⋯ , α r ) W=span(\alpha_1,\cdots,\alpha_r) W=span(α1,⋯,αr)
a. 基性质
-
设 W 是r维子空间 ( d i m W = r dim W=r dimW=r) ,则W中任 r+1 个向量必线性相关
证 明 : 设 W 的 基 为 α 1 , ⋯ , α r , 任 取 β 1 , ⋯ , β r , β r + 1 ∈ W , 可 知 每 个 β 可 有 α 基 向 量 表 示 , 即 向 量 组 { β 1 , ⋯ , β r } 的 秩 ≤ r ( α q , ⋯ , α r ) = r ≤ r + 1 , 故 { β } 向 量 组 线 性 相 关 \begin{aligned} 证明:&设W的基为 \alpha_1,\cdots,\alpha_r,任取\beta_1,\cdots,\beta_r,\beta_{r+1} \in W,可知每个\beta 可有\alpha 基向量表示,即\\ &向量组\{\beta_1,\cdots,\beta_r\}的秩\le r(\alpha_q,\cdots,\alpha_r) =r\le r+1,故\{\beta\}向量组线性相关 \end{aligned} 证明:设W的基为α1,⋯,αr,任取β1,⋯,βr,βr+1∈W,可知每个β可有α基向量表示,即向量组{β1,⋯,βr}的秩≤r(αq,⋯,αr)=r≤r+1,故{β}向量组线性相关 -
W的基 [ α 1 , ⋯ , α r ] [\alpha_1,\cdots,\alpha_r] [α1,⋯,αr] 必是向量组W的一个极大无关组,从而 d i m W = r ( W ) dim W=r(W) dimW=r(W)
5.1.4 A产生的子空间
a. 列空间(值域)
A
=
A
m
,
n
A=A_{m,n}
A=Am,n 的值域
R
(
A
)
=
{
全
体
y
=
A
x
∣
x
∈
C
n
}
R(A)=\{全体y=Ax\vert x\in C^n\}
R(A)={全体y=Ax∣x∈Cn}
A
=
A
m
,
n
=
(
α
1
,
⋯
,
α
n
)
,
其
中
α
i
∈
C
m
,
X
=
(
x
1
⋮
x
n
)
∈
C
n
Y
=
A
X
=
x
1
α
1
+
⋯
+
x
n
α
n
=
(
x
1
α
1
,
⋯
,
x
n
α
n
)
为
A
的
生
成
列
空
间
\begin{aligned} &A=A_{m,n}=(\alpha_1,\cdots,\alpha_n),其中\alpha_i\in C^m ,X=\left( \begin{matrix} x_1\\\vdots\\x_n \end{matrix} \right)\in C^n\\ &Y=AX=x_1\alpha_1+\cdots+x_n\alpha_n=\left(x_1\alpha_1,\cdots,x_n\alpha_n\right)为A的生成列空间 \end{aligned}
A=Am,n=(α1,⋯,αn),其中αi∈Cm,X=⎝⎜⎛x1⋮xn⎠⎟⎞∈CnY=AX=x1α1+⋯+xnαn=(x1α1,⋯,xnαn)为A的生成列空间
即对
C
n
C^n
Cn 中的所有列向量进行A变换产生的列生成空间,记为
R
(
A
)
=
{
y
=
x
1
α
1
+
⋯
+
x
n
α
n
∣
X
∈
C
n
}
R(A)=\{y=x_1\alpha_1+\cdots+x_n\alpha_n\vert X\in C^n\}
R(A)={y=x1α1+⋯+xnαn∣X∈Cn}
R ( A ) = L ( α 1 , ⋯ , α n ) R(A)=L(\alpha_1,\cdots,\alpha_n) R(A)=L(α1,⋯,αn) 或 R ( A ) = s p a n ( α 1 , ⋯ , α n ) R(A)=span(\alpha_1,\cdots,\alpha_n) R(A)=span(α1,⋯,αn)
维数=秩, d i m R ( A ) = r ( A ) = r dimR(A)=r(A)=r dimR(A)=r(A)=r
b. A的核空间
A = A m , n A=A_{m,n} A=Am,n 的核空间为 N ( A ) = { x ∈ C n ∣ A x = 0 } ⊂ C n N(A)=\{x\in C^n\vert Ax=0\}\subset C^n N(A)={x∈Cn∣Ax=0}⊂Cn (解空间)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RiaRmgni-1669511800255)(5.正规方程/image-20221126220144196.png)]
维数公式
d i m N ( A ) + d i m R ( A ) = n dim N(A)+dim R(A)=n dimN(A)+dimR(A)=n 或 d i m N ( A ) + r ( A ) = n dim N(A)+r(A)=n dimN(A)+r(A)=n ,即 d i m N ( A ) = n − r ( A ) dim N(A)=n-r(A) dimN(A)=n−r(A)
5.1.5 正交引理
a. C m C^m Cm 中正交引理(列空间中向量的正交向量)
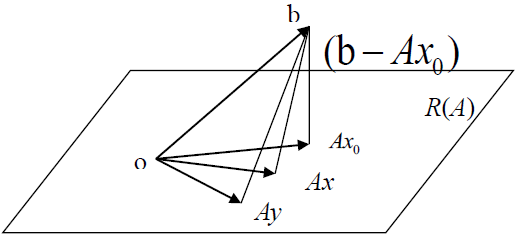
任取 b ∈ C m b\in C^m b∈Cm ,令 x 0 = A + b ∈ C n x_0=A^+b\in C^n x0=A+b∈Cn ,则 ( b − A x 0 ) ⊥ A x , ∀ x ∈ C n (b-Ax_0)\bot Ax,\forall x\in C^n (b−Ax0)⊥Ax,∀x∈Cn

正交子空间
设 A ∈ C m × n A\in C^{m\times n} A∈Cm×n ,则有 N ( A ) ⊥ R ( A H ) N(A)\bot R(A^H) N(A)⊥R(AH) ,且 N ( A H ) ⊥ R ( A ) N(A^H)\bot R(A) N(AH)⊥R(A)
证明:
任
取
y
∈
N
(
A
)
,
即
满
足
A
y
=
0
。
任
取
A
H
x
∈
R
(
A
H
)
,
若
证
N
(
A
)
⊥
R
(
A
H
)
,
则
只
需
证
(
y
,
A
H
x
)
=
0
,
∵
(
y
,
A
H
x
)
=
(
A
H
x
)
H
y
=
x
H
A
y
=
X
H
(
A
y
)
=
X
H
0
=
0
,
即
有
N
(
A
)
⊥
R
(
A
H
)
\begin{aligned} &任取 y\in N(A),即满足Ay=0。任取A^Hx\in R(A^H),若证N(A)\bot R(A^H) ,则只需证(y,A^Hx)=0,\\ &\because (y,A^Hx)=(A^Hx)^Hy=x^HAy=X^H(Ay)=X^H0=0,即有N(A)\bot R(A^H) \end{aligned}
任取y∈N(A),即满足Ay=0。任取AHx∈R(AH),若证N(A)⊥R(AH),则只需证(y,AHx)=0,∵(y,AHx)=(AHx)Hy=xHAy=XH(Ay)=XH0=0,即有N(A)⊥R(AH)
b. C n C^n Cn 中正交引理(核空间的正交向量)
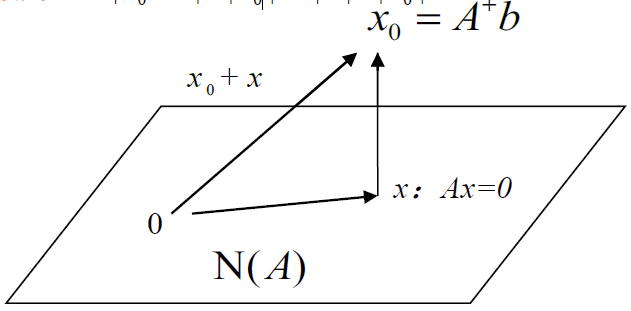
任取 b ∈ C m b\in C^m b∈Cm ,令 x 0 = A + b ∈ C n x_0=A^+b\in C^n x0=A+b∈Cn ,则 x 0 ⊥ N ( A ) x_0\bot N(A) x0⊥N(A) ,即 x 0 ⊥ y , y ∈ { y ∣ A y = 0 } x_0\bot y ,y\in \{y\vert Ay=0\} x0⊥y,y∈{y∣Ay=0}
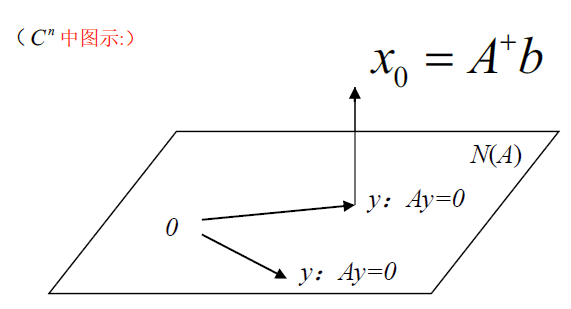
证明:
由
于
y
在
A
的
解
空
间
,
则
已
知
A
y
=
0
,
要
证
x
0
⊥
y
,
即
证
内
积
(
y
,
x
0
)
=
0
(
y
,
x
0
)
=
x
0
H
y
=
(
A
+
b
)
H
y
=
(
A
+
A
A
+
b
)
H
y
=
(
A
+
b
)
H
(
A
+
A
)
H
y
=
(
A
+
b
)
H
A
+
A
y
=
0
⇒
x
0
⊥
y
,
即
x
0
⊥
N
(
A
)
\begin{aligned} &由于y在A的解空间,则已知Ay=0,要证x_0\bot y,即证内积(y,x_0)=0\\ &(y,x_0)=x_0^Hy=(A^+b)^Hy=(A^+AA^+b)^Hy=(A^+b)^H(A^+A)^Hy=(A^+b)^HA^+Ay=0\\ &\Rightarrow x_0\bot y,即 x_0\bot N(A) \end{aligned}
由于y在A的解空间,则已知Ay=0,要证x0⊥y,即证内积(y,x0)=0(y,x0)=x0Hy=(A+b)Hy=(A+AA+b)Hy=(A+b)H(A+A)Hy=(A+b)HA+Ay=0⇒x0⊥y,即x0⊥N(A)
x 0 = A + b x_0=A^+b x0=A+b 为 A x = b Ax=b Ax=b 的最小解
令 x 0 = A + b , ∀ x ∈ N ( A ) , A y = b 有 通 解 y = x 0 + t x , 而 ∣ y ∣ 2 = ∣ x 0 + x ∣ 2 ∵ x 0 ⊥ x , 由 勾 股 定 理 ⇒ ∣ x 0 + x ∣ 2 = ∣ x 0 ∣ 2 + ∣ x ∣ 2 ≥ ∣ x 0 ∣ 2 \begin{aligned} &令x_0=A^+b,\forall x\in N(A),Ay=b有通解y= x_0+tx,而\vert y\vert^2=\vert x_0+x\vert^2\\ &\because x_0\bot x,由勾股定理\Rightarrow \vert x_0+x\vert^2=\vert x_0\vert^2+\vert x \vert^2\ge \vert x_0\vert^2 \end{aligned} 令x0=A+b,∀x∈N(A),Ay=b有通解y=x0+tx,而∣y∣2=∣x0+x∣2∵x0⊥x,由勾股定理⇒∣x0+x∣2=∣x0∣2+∣x∣2≥∣x0∣2