从上一讲 测距 末尾的frame讲起。我们知道一个chirp对应了一个采样后的IF信号，我们将这些采样后的IF信号按chirp的次序排列成一个帧（frame），这就得到了我们实际中接收后处理的FMCW信号。

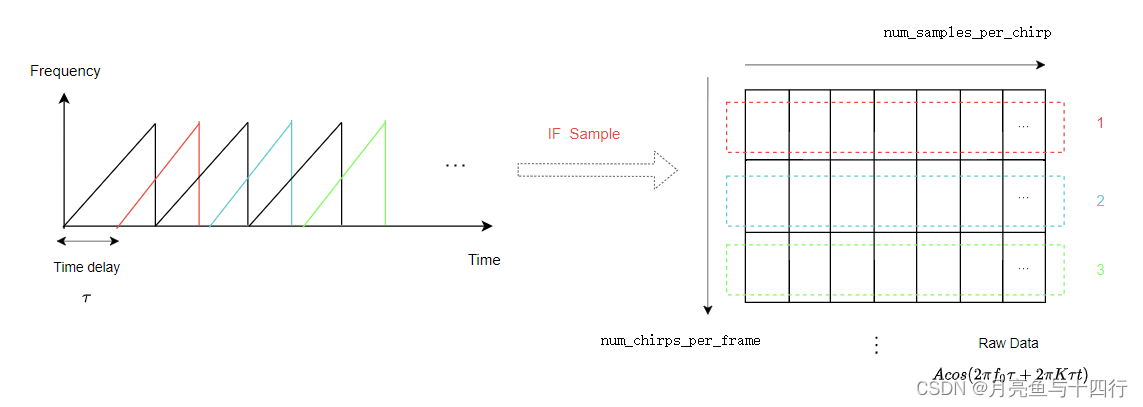
由于chirp的发射返回时间很短，所以我们称其所在时间维度为快时间（fast time）维，而相邻的chirp间存在一个chirp repetition time（CRT）相对较慢，于是我们将其所在时间维度为慢时间（slow time）维。借一幅《Soli: Ubiquitous Gesture Sensing with Millimeter》文中的图，可以对raw signal有一个直观的认识。

相位差的周期性

我们首先对FFT得到的频率谱做一个分析，其分为两部分，幅度部分和相位部分，幅度部分可以表示此处频率的强弱，相位部分表示的是此频率对应的相位。那么，对于，对做完range FFT后的frame矩阵而言，其fast time维度就转换成了range维度。

对于在某一个 range bin上的物体，我们已经知道其距离表示为
$$d_{target}=\frac{c}{2K}{f}_{peak}$$
这个距离的解我们知道是通过IF信号中频率部分$2\pi K\tau$得到的，而我们现在关注其相位部分$2\pi f_0\tau$。

$$x_{IF}(t)=A\cos (2\pi K\tau t+2\pi f_o\tau )$$

由于
$$\tau =\frac{2d}{c}$$

故相位$\varphi$
$$\varphi =2\pi f_o\frac{2d}{c}=\frac{4\pi f_o}{c}d$$

如果在这个range bin中的物体正在运动，那么每隔一个chirp的周期$CRT$，物体就会发生一个微动位移，而这个微动位移将造成相位较为剧烈的变化，即
$$\Delta \varphi =\frac{4\pi f_o}{c}\Delta d=\frac{4\pi f_0}{c}v\cdot CRT$$

如果我们将这个$CRT$看作一种采样，那么，对$\varphi$的变化进行分析，将能提取到有效的速度$v$的信息，这也正是我们采用frame传输的原因——获得速度信息。 这种视角先按下不表，最后再述。

我们也可将这个过程看作是相位差的周期性运动，那么我们对其进行FFT分析，也将得到这个周期性的相位差信息。

进一步转换到速度维，就有

$$v=\frac{c}{4\pi f_o\cdot CRT}\Delta \varphi =\frac{\lambda }{4\pi \cdot CRT}\Delta \varphi$$

于是我们要做的Doppler FFT 或者说 Velocity FFT即是取出Range FFT某个range bin对应的一列slow time数据进行FFT。

多普勒效应

那么问题来了，为什么叫Doppler FFT呢？在基本的物理学中，我们曾学习过基本的多普勒效应。举一个生活中的例子，你在街上听到一辆警车向你呼啸而来，你听到警笛的声音是越来越急的（这对应的即是声波的频率越来越高），而当警车越来越远时，你听的警笛是越来越疏的（这对应的即是声波的频率越来越低）。

在这里，我们用一个移动通信中描述移动台所造成的多普勒频偏公式（见Rappaport书中的123页），即
$$f_d=\frac{v}{\lambda }\cos \theta$$

在FMCW雷达考虑的场景中，取径向速度，即 $\cos \theta =1$，同时由于电波一发一收，于是造成的$f_d$为

$$f_d=2\frac{v}{\lambda }$$

进一步代入 v 的公式转换为

$$f_d=\frac{\Delta \varphi }{2\pi \cdot CRT}$$

值得指出的是，主频率部分亦会由于物体的运动产生频偏。但当物体的距离d发生微小的变化时，IF signal 信号的相位变化非常明显，而频率的变化并不显著，远远达不到在CRT的时间内，区分信号的频率。 即相位变化对微动位移有着敏感性。

我们不如用TI教程中的例子来感性认识一下：取 $\lambda =4mm$，$CRT=40\mu s$，$K=50MHz/\mu s$，当物体发生一个1mm的微动位移时，有：

$$相位变化\Delta \varphi =\frac{4\pi \Delta d}{\lambda }=\pi =180^{\circ }$$

$$频率变化\Delta f=\frac{2K}{c}\Delta d=333Hz$$

而这个频偏在slow time的频率轴引起的变化其实并不大，即
$$\Delta f\cdot CRT=333\times 40\times 10^{-6}=0.013cycles$$

最大速度与速度分辨率

最大速度

由于$\Delta \varphi$ 的限制，给出了最大速度的限制，即
$$-\pi <\Delta \varphi <\pi$$
于是
$$-\frac{\lambda }{4\cdot CRT}<v<\frac{\lambda }{4\cdot CRT}$$

感性认识一下，比如用 $5mm$ 的毫米波雷达，再用 $100\mu s$ 的CRT，此时能达到的最大速度为
$$v_{max}=\frac{\lambda }{4\cdot CRT}=12.5m/s$$

速度分辨率

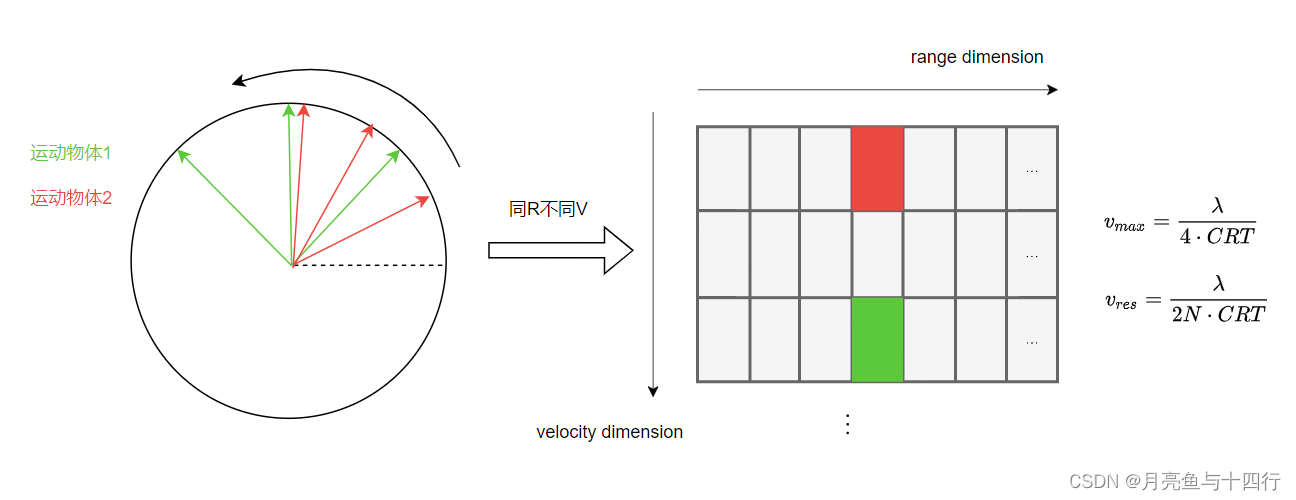
继续借用TI教程里的一张图（这里定义 $\omega =\Delta \varphi$），容易发现，速度分辨率与我们的在数字域上的角速度分辨率有关，由于
$$\Delta \omega =\frac{2\pi }{N}radians/sample=\frac{1}{N}cycles/sample$$

于是就有
$$\Delta v=\frac{\lambda }{4\pi \cdot CRT}\Delta \omega =\frac{\lambda }{2N\cdot CRT}$$

仍用最大速度中的测算数据，并取 N = 512，我们感性认识到此时的速度分辨率为：
$$v_{res}=\frac{\lambda }{2N\cdot CRT}=0.0488m/s$$

基于CRT的采样视角

如果我们基于CRT的采样视角去理解这个相位变化，那么对于式子
$$\Delta \varphi =\frac{4\pi f_o}{c}\Delta d=\frac{4\pi f_0}{c}v\cdot CRT$$
我们两边同除 $CRT$，就有：
$$\frac{\Delta \varphi }{CRT}=\frac{4\pi f_0}{c}v$$
根据微分学的知识，我们知道左边可理解为对$\varphi$的微分，即
$$w=\frac{d\varphi }{dt}=2\pi f_{peak}$$
于是就有：
$$f_{peak}=2\frac{v}{\lambda }$$
这个式子说明，从频率轴去看，此时直接测得的就是多普勒频偏。进一步就有：
$$v=\frac{\lambda }{2}{f}_{peak}$$

由于此时 $CRT$ 的倒数即是我们等效的采样率。于是，频率分辨率的范围就在
$$-\frac{1}{2\cdot CRT}<f_{peak}<\frac{1}{2\cdot CRT}$$
于是，可得速度的测量范围为
$$-\frac{\lambda }{4\cdot CRT}<v<\frac{\lambda }{4\cdot CRT}$$
和速度的分辨率
$$v_{res}=\frac{\lambda }{2}{f}_{res}=\frac{\lambda }{2N\cdot CRT}$$

这种视角个人兴趣所至，以增参考。最后，同样用一张图结束本节的内容。