Stochastic Approximation and Stochastic Gradient Descent

举个例子

首先回顾mean estimation：

• 考虑一个random variable X。
• 目标是估计$\mathbb{E}[X]$
• 假设已经有了一系列随机独立同分布的样本 { x i } i = 1 N \{x_i\}_{i=1}^N {xi​}i=1N​
• X的expection可以被估计为$$\mathbb{E}[X]\approx \bar{x}:=\frac{1}{N}\sum _{i=1}^N{x}_i$$

已经知道这个估计的基本想法是Monte Carlo estimation，以及$\bar{x}\to \mathbb{E}$，随着$N\to \infty$。这里为什么又要关注mean estimation，那是因为在强化学习中许多value被定义为means，例如state/action value。

新的问题：如何计算mean $barx$：$$\mathbb{E}[X]\approx \bar{x}:=\frac{1}{N}\sum _{i=1}^N{x}_i$$
我们有两种方式：

• 第一种方法：简单地，收集所有样本，然后计算平均值。但是该方法的缺点是如果样本是一个接一个的被收集，那么就必须等待所有样本收集完成才能计算
• 第二种方法：可以克服第一种方法的缺点，用一种incremental（增量式）和iterative（迭代式）的方式计算average。

具体地，假设$$w_{k+1}=\frac{1}{k}\sum _{i=1}^k{x}_i,k=1,2,...$$然后有$$w_k=\frac{1}{k-1}\sum _{i=1}^{k-1}{x}_i,k=2,3,...$$，我们要建立$w_k$和$w_{k+1}$之间的关系，用$w_k$表达$w_{k+1}$：$$w_{k+1}=\frac{1}{k}\sum _{i=1}^k{x}_i=\frac{1}{k}(\sum _{i=1}^{k-1}{x}_i+x_k)=\frac{1}{k}((k-1)w_k+x_k)=w_k-\frac{1}{k}(w_k-x_k)$$因此，获得了如下的迭代算法：$$w_{k+1}=w_k-\frac{1}{k}(w_k-x_k)$$
我们使用上面的迭代算法增量式地计算x的mean：

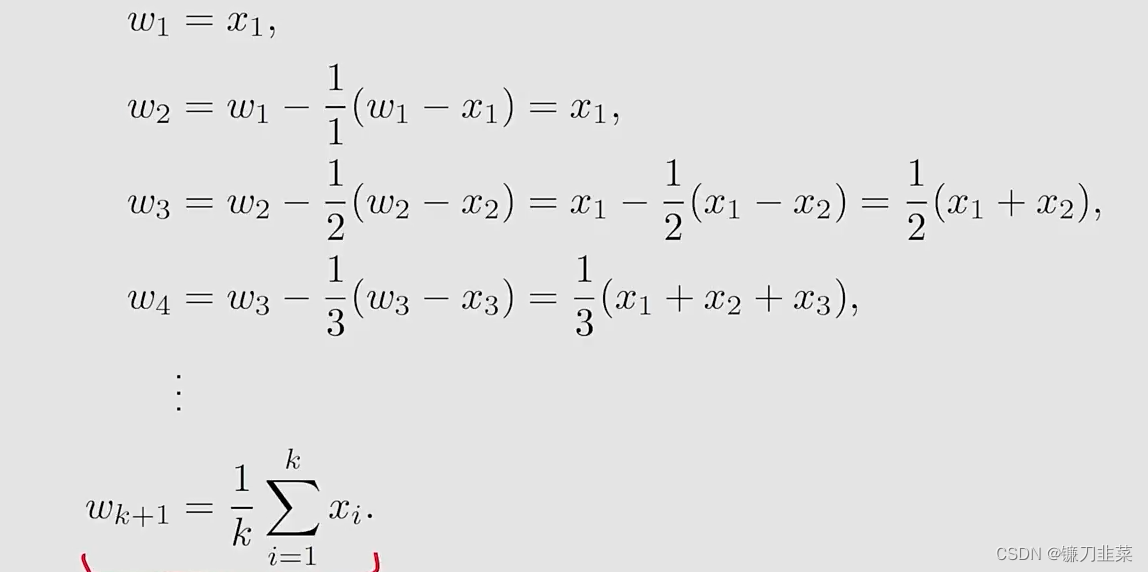
这样就得到了一个求平均数的迭代式的算法。算法的优势是在第k步的时候不需要把前面所有的$x_i$全部加起来再求平均，可以在得到一个样本的时候立即求平均。另外这个算法也代表了一种增量式的计算思想，在最开始的时候因为$k$比较小，$w_k\ne \mathbb{E}[X]$，但是随着获得样本数的增加，估计的准确度会逐渐提高，也就是$w_k\to \mathbb{E}[X]\text{ as }k\to N$。

更进一步地，将上述算法用一个更泛化的形式表示为：$$w_{k+1}=w_k-{\alpha }_k(w_k-x_k)$$，其中$1/k$被替换为${\alpha }_k>0$。

• 该算法是否会收敛到mean $\mathbb{E}[X]$？答案是Yes，如果 { α k } \{\alpha_k\} {αk​}满足某些条件的时候
• 该算法也是一种特殊的SA algorithm和stochastic gradient descent algorithm

Robbins-Monro algorithm

算法描述

Stochastic approximation (SA):

• SA代表了一大类的stochastic iterative algorithm，用来求解方程的根或者优化问题。
• 与其他求根相比，例如gradient-based method， SA的强大之处在于：它不需要知道目标函数的表达式，也不知道它的导数或者梯度表达式。

Robbins-Monro (RM) algorithm:

• This is a pioneering work in the field of stochastic approximation.
• 著名的stochastic gradient descent algorithm是RM算法的一个特殊形式。
• It can be used to analyze the mean estimation algorithms introduced in the beginning。

举个例子

问题声明：假设我们要求解下面方程的根$$g(w)=0$$，其中$w\in \mathbb{R}$是要求解的变量，$g:\mathbb{R}\to \mathbb{R}$是一个函数.

• 许多问题最终可以转换为这样的求根问题。例如，假设$J(w)$是最小化的一个目标函数，然后，优化问题被转换为$$g(w)={\nabla }_{w}J(w)=0$$
• 另外可能面临$g(w)=c$，其中$c$是一个常数，这样也可以将其转换为上述等式，通过将$g(w)-c$写为一个新的函数。

那么如何求解$g(w)=0$？

• 如果$g$的表达式或者它的导数已知，那么有许多数值方法可以求解
• 如果函数$g$的表达式是未知的？例如the function由一个artificial neural network表示

这样的问题可以使用Robbins-Monro(RM)算法求解：$$w_{k+1}=w_k-a_k\tilde{g}(w_k,{\eta }_k),k=1,2,3,...$$其中

• $w_k$是root的第k次估计
• $\tilde{g}(w_k,{\eta }_k)=g(w_k)+{\eta }_k$是第k次带有噪声的观测
• $a_k$是一个positive coefficient

函数$g(w)$是一个black box！也就是说该算法依赖于数据：

• 输入序列: { w k } \{w_k\} {wk​}
• 噪声输出序列： { g ~ ( w k , η k ) } \{\tilde{g}(w_k,\eta_k)\} {g~​(wk​,ηk​)}

这里边的哲学思想：不依赖model，依靠data！这里的model就是指函数的表达式。

收敛性分析

为什么RM算法可以找到$g(w)=0$的解？
首先给出一个直观的例子：

• $g(w)=tanh(w-1)$
• $g(w)=0$的true root是$w\ast =1$
• 初始值：$w_1=2,a_k=1/k,{\eta }_k=0$（为简单起见，不考虑噪音）

在本例中RM算法如下：$$w_{k+1}=w_k-a_{k}g(w_k)$$
当${\eta }_k=0$的时候$\tilde{g}(w_k,{\eta }_k)=g(w_k)$。

模拟仿真结果：$w_k$收敛到true root $w\ast =1$。

直观上：$w_{k+1}$比$w_k$更接近于$w\ast$

• 当$w_k>w\ast$，有$g(w_k)>0$，那么$w_{k+1}=w_k-a_{k}g(w_k)<w_k$，因此$w_{k+1}$比$w_k$更接近于$w\ast$
• 当$w_k<w\ast$，有$g(w_k)<0$，那么$w_{k+1}=w_k-a_{k}g(w_k)>w_k$，因此$w_{k+1}$比$w_k$更接近于$w\ast$

上面的分析是基于直观的，但是不够严格。一个严格收敛的结果如下：

在RM算法中，如果上面的条件满足，那么$w_k$就会收敛到$w\ast$，$w\ast$就是$g(w)=0$的一个解。第一个条件是关于g(w)的梯度要求，第二个条件是关于$a_k$系数的要求，第三个条件是关于这个${\eta }_k$，就是测量误差的要求。

这三个条件的解释：

• 条件1：$0<c_1\le {\nabla }_{k}g(w)\le c_2$对于所有的$w$
  
• 条件2：${\sum }_{k=1}^{\infty }{a}_k=\infty$且${\sum }_{k=1}^{\infty }{a}_k^2<\infty$
  
• 条件3：$\mathbb{E}[{\eta }_k|{\mathcal{H}}_k]=0$并且$\mathbb{E}[{\eta }_k^2|{\mathcal{H}}_k]<\infty$
  

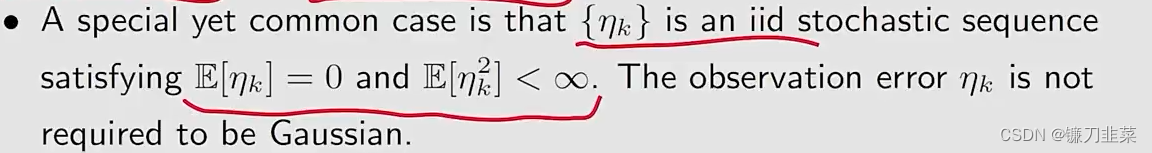
对第二个条件进行讨论：$$\sum _{k=1}^{\infty }{a}_k^2<\infty \text{ , }\sum _{k=1}^{\infty }{a}_k=\infty$$

• 首先：${\sum }_{k=1}^{\infty }{a}_k^2<\infty$表明随着$k\to \infty$，$a_k\to 0$
• 为什么这个条件重要呢？
  因为$$w_{k+1}-w_k=-a_k\tilde{g}(w_k,{\eta }_k)$$
  • 如果$a_k\to 0$，那么$a_k\tilde{g}(w_k,{\eta }_k)\to 0$，因此$w_{k+1}-w_k\to 0$
  • we need the fact that $w_{k+1}-w_k\to 0$ 如果$w_k$最终收敛
  • 如果$w_k\to w\ast$，那么$g(w_k)\to 0$和$\tilde{g}(w_k,{\eta }_k)$由${\eta }_k$确定。
• 第二，${\sum }_{k=1}^{\infty }{a}_k=\infty$表明$a_k$不应当太快收敛到0.
• 为什么这个条件重要呢？
• 根据$w_2=w_1-a_1\tilde{g}(w_1,{\eta }_1)$, $w_3=w_2-a_2\tilde{g}(w_2,{\eta }_2)$, …, $w_{k+1}=w_k-a_k\tilde{g}(w_k,{\eta }_k)$得出$$w_{\infty }-w_1=\sum _{k=1}^{\infty }{a}_k\tilde{g}(w_k,{\eta }_k)$$。假定$w_{\infty }=w\ast$。如果${\sum }_{k=1}^{\infty }{a}_k<\infty$，那么${\sum }_{k=1}^{\infty }{a}_k\tilde{g}(w_k,{\eta }_k)$可能是有界的。然后，如果初始猜测$w_1$任意选择远离$w\ast$，那么上述等式可能是不成立的（invalid）。

那么问题来了，什么样的$a_k$能够满足这样两个条件呢？${\sum }_{k=1}^{\infty }{a}_k=\infty$且${\sum }_{k=1}^{\infty }{a}_k^2<\infty$
一个典型的序列是$$a_k=\frac{1}{k}$$

• 在数学上$$\underset{n\to \infty }{\lim }(\sum _{k=1}^n\frac{1}{n}-\ln n)=k$$其中$k\approx 0.577$，称为Euler-Mascheroni常数（也称为Euler常数）
• 另一个数学上的结论是：$$\sum _{k=1}^{\infty }\frac{1}{k^2}=\frac{{\pi }^2}{6}<\infty$$极限${\sum }_{k=1}^{\infty }$在数论中也有一个特定的名字：Basel problem。

如果上面三个条件不满足，则RM算法将不再工作，例如：

在许多RL算法中，$a_k$经常选择一个非常小的常数（sufficiently small constant），尽管第二个条件不满足，但是该RM算法仍然可以工作。

将RM算法用于mean estimation

回顾本文最初的mean estimation算法$$w_{k+1}=w_k-{\alpha }_k(w_k-x_k)$$
我们知道：

• 如果${\alpha }_k=1/k$，那么$w_{k+1}=1/k{\sum }_{i=1}^k{x}_i$
• 如果${\alpha }_k$不是$1/k$，收敛性没办法分析。

现在我们证明这个算法是一个特殊的RM算法，它的收敛性就能够得到了。
1）考虑一个函数$$g(w)\doteq w-\mathbb{E}[X]$$我们的目标是求解$g(w)=0$，这样，我们就可以得到$\mathbb{E}[X]$
2）我们不知道X，但是可以对X进行采样，因此我们得到的观察是$$\tilde{g}(w,x)\doteq w-x$$，注意

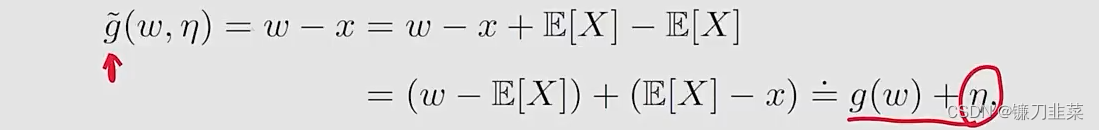
3）求解$g(x)=0$的RM算法是$$w_{k+1}=w_k-{\alpha }_k\tilde{g}(w_k,{\eta }_k)=w_k-{\alpha }_k(w_k-x_k)$$,这就是之前给出的mean estimation算法。

Dvoretzkys convergence theorem

• 这是一个比RM定理更一般化的结论，可以用来证明RM定理
• 它可以直接用来分析mean estimation problem
• 它的一个扩展可以用来分析Q-learning和TD learning算法。

Stochastic gradient descent

stochastic gradient descent(SGD)算法在机器学习和强化学习的许多领域中广泛应用；SGD也是一个特殊的RM算法，而且mean estimation algorithm是一个特殊的SGD算法。

算法描述

假设我们的目标是求解下面优化问题:$$\underset{w}{\min }J(w)=\mathbb{E}[f(w,X)]$$

• $w$是被优化的参数
• $X$是一个随机变量，The expection实际上就是针对这个$X$进行计算的
• $w$和$X$可以是标量或者向量，函数$f(\cdot )$是一个标量。

有三种方法求解：
Method 1: gradient descent (GD)

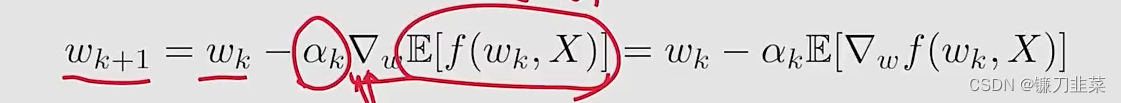
问题是the expected value is difficult to obtain。
Method 2: batch gradient descent (BGD)

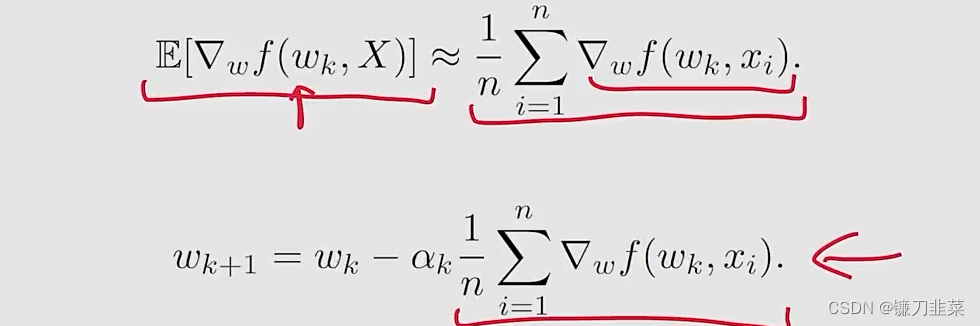
问题是对于每个$w_k$，在每次迭代中需要许多次采样。
Method 3: stochastic gradient descent (SGD):

SGD与前面两种算法相比：

• 与gradient descent算法相比，将true gradient $\mathbb{E}[{\nabla }_{w}f(w_k,X)]$替换为stochastic gradient ${\nabla }_{w}f(w_k,x_k)$
• 与batch gradient descent算法相比，令$n=1$。

示例和应用

考虑下面的一个优化问题：

其中：

有三个练习：

1. 证明最优解是$w\ast =\mathbb{E}[X]$
2. 用GD算法求解这个问题
3. 用SGD算法求解这个问题

首先看第一个练习：
对$J(w)$求梯度，使其等于0，即可得到最优解，因此有${\nabla }_{w}J(w)=0$，然后根据公式，得到$\mathbb{E}[{\nabla }_{w}f(w,X)]=0$，然后得到$\mathbb{E}[w-X]=0$，由于w是一个常数，因此$w=\mathbb{E}[X]$。

第二个联系的答案是：

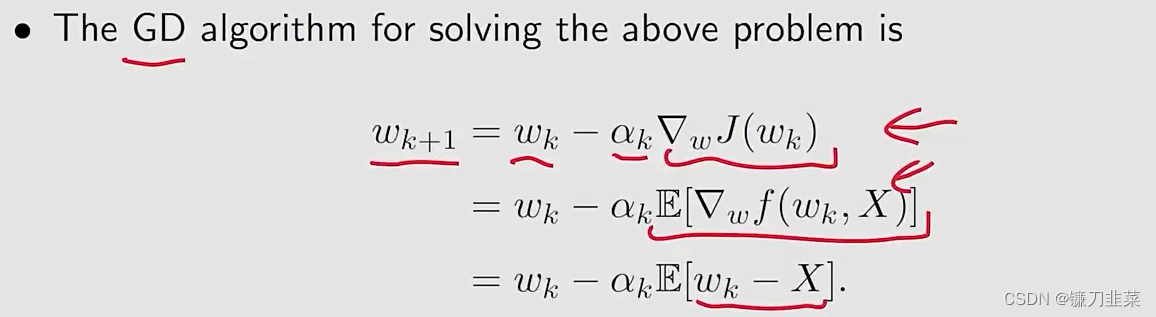
相应的，使用SGD算法求解上面问题：

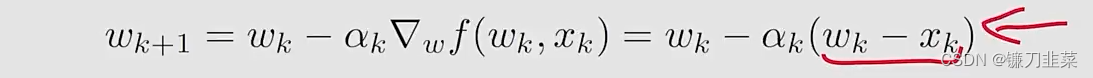
收敛性分析

从GD到SGD：

${\nabla }_{w}f(w_k,x_k)$被视为$\mathbb{E}[{\nabla }_{w}f(w_k,X)]$的一个noisy measurement：

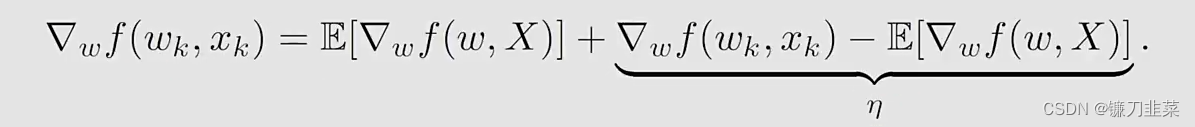
不管怎样，由于$${\nabla }_{w}f(w_k,x_k)\ne \mathbb{E}[{\nabla }_{w}f(w_k,X)]$$，是否基于SGD随着k趋近于无穷，$w_k\to w\ast$？答案是肯定的。

这里的方式证明SGD是一个特殊的RM算法，自然地得到收敛性。SGD的目标是最小化$$J(w)=\mathbb{E}[f(w,X)]$$
这个问题可以转换为一个root-finding问题：$${\nabla }_{w}J(W)=\mathbb{E}[{\nabla }_{w}f(w,X)]=0$$
令$$g(w)={\nabla }_{w}J(W)=\mathbb{E}[{\nabla }_{w}f(w,X)]$$，那么SGD的目标就是找到满足$g(w)=0$的根。

这里使用RM算法求解，因为g(w)的表达式未知，所以要用到数据。what we can measure is

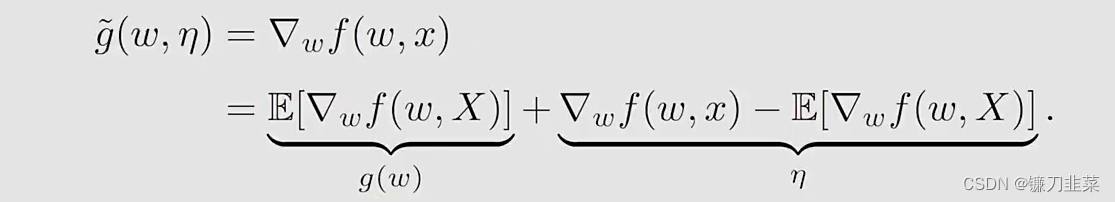
然后，RM算法求解$g(w)=0$就得到

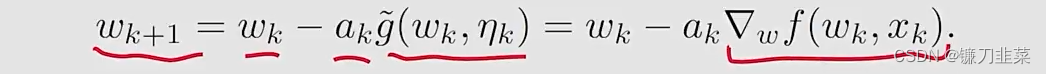
• It is exacely the SGD algorithm
• 因此，SGD是一个特殊的RM算法。

因为SGD算法是一个特殊的RM算法，它的收敛性遵从：

收敛模式

问题：由于stochastic gradient是随机的，那么approximation是不精确的，是否SGD的收敛性是slow或者random？
为了回答这个问题，我们考虑在stochastic和batch gradients之间的一个relative error:

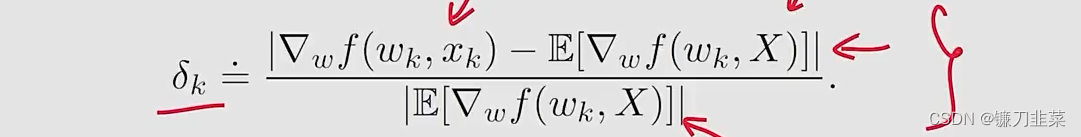
由于$\mathbb{E}[{\nabla }_{w}f(w\ast ,X)]=0$，我们有：

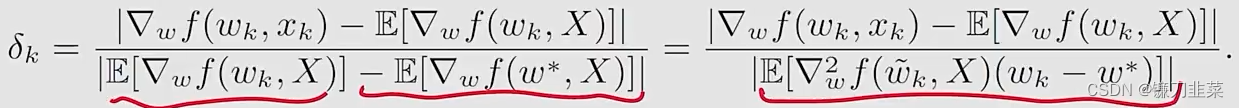
其中后面等式的分母使用了一个mean value theorem（中值定理），并且${\tilde{w}}_k\in [w_k,w\ast ]$

假设$f$是严格凸的，满足$${\nabla }_w^{2}f\ge c>0$$对于所有的$w,X$，其中$c$是一个positive bound。

然后，${\delta }_k$的证明就变为了

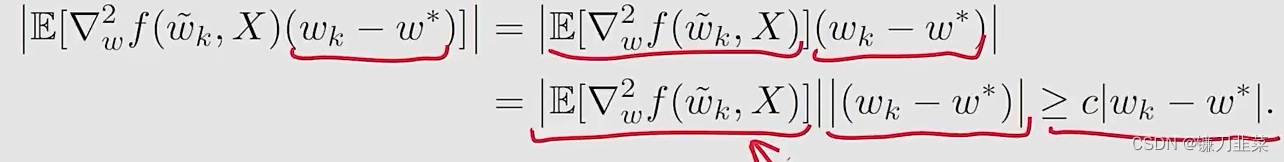
然后把这个分母的性质带入刚才的relative error公式，就得到

再看上面的式子：

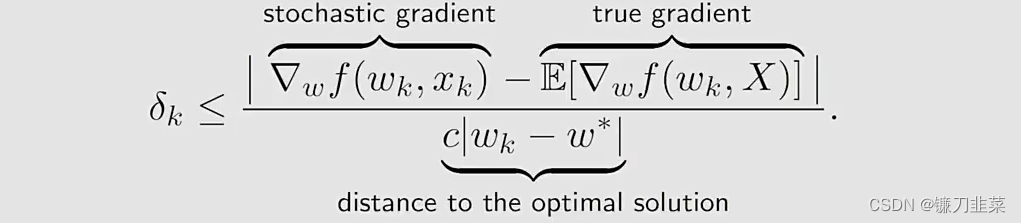
这个公式也表明了SGD的一个有趣的收敛模式：

• relative error ${\delta }_k$与$|w_k-w\ast |$成反比
• 当$|w_k-w\ast |$比较大时，${\delta }_k$较小，SGD的表现与GD相似（behaves like）
• 当$w_k$接近$w\ast$，相对误差可能较大，收敛性在$w\ast$的周边存在较多的随机性。

考虑一个例子：
Setup:

Result:

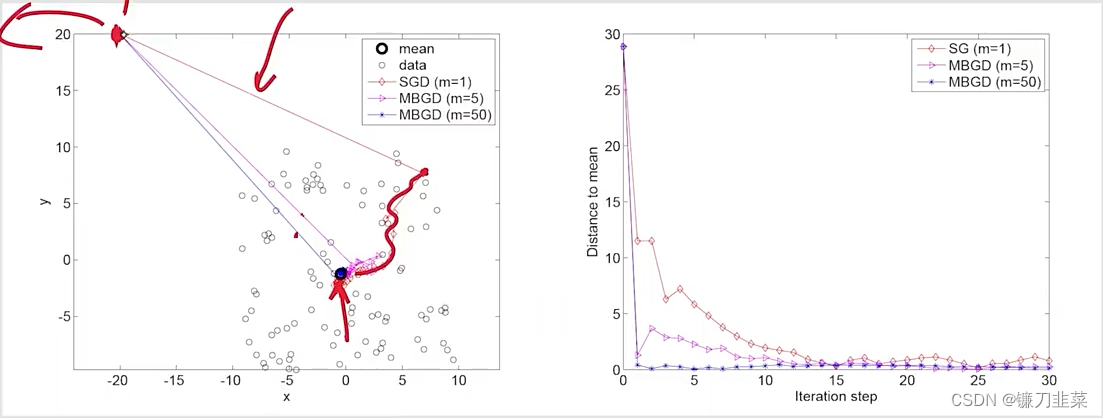
MBGD:mini-batch gradient descent

• 尽管在初始的时候，mean远离true value，但是SGD estimate can approach the neighborhood of the true value fast.
• 当estimate接近true value，它具有一定程度的随机性，但是仍然逐渐靠近the true value

一个确定性公式

在之前介绍的SGD的formulation中，涉及random variable和expectation。但是在学习其他材料的时候可能会遇到一个SGD的deterministic formulation，不涉及任何random variables。

同样地，考虑这样一个优化问题：$$\underset{w}{\min }J(w)=\frac{1}{n}\sum _{i=1}^{n}f(w,x_i)$$

• $f(w,x_i)$是一个参数化的函数
• $w$是需要被优化的参数
• 一组实数 { x i } i = 1 n \{x_i\}_{i=1}^n {xi​}i=1n​，其中$x_i$不必是任意random variable的一个采样，反正就是一组实数。

求解这个问题的gradient descent算法如下：

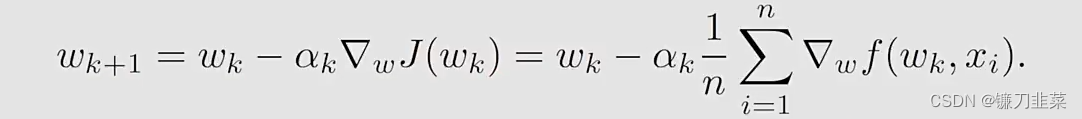
假设这样的一个实数集合比较大，每次只能得到一个$x_i$，在这种情况下，可以使用下面的迭代算法：$$w_{k+1}=w_k-{\alpha }_k{\nabla }_{w}f(w_k,x_k)$$
那么问题来了：

• 这个算法是SGD吗？它没有涉及任何random variable或者expected values.
• 我们该如何定义这样一组实数 { x i } i = 1 n \{x_i\}_{i=1}^n {xi​}i=1n​? 是应该将它们按照某种顺序一个接一个地取出？还是随机地从这个集合中取出？

回答上面问题的思路是：我们手动地引入一个random variable，并将SGD从deterministic formulation转换为stochastic formulation。
具体地，假设一个$X$是定义在集合 { x i } i = 1 n \{x_i\}_{i=1}^n {xi​}i=1n​的random variable。假设它的概率分布是均匀的，即$$p(X=x_i)=1/n$$
然后，这个deterministic optimization problem变成了一个stochastic one：

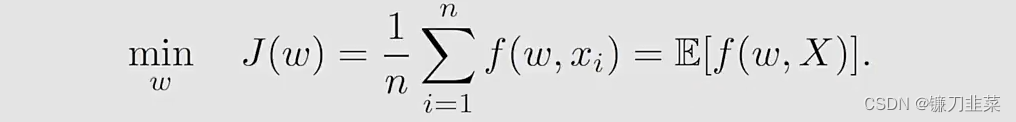
• 上面等式的后面是strict，而不是approximate。因此，这个算法是SGD。
• The estimate converges if $x_k$ is uniformly and independently sampled from { x i } i = 1 n \{x_i\}_{i=1}^n {xi​}i=1n​. $x_k$ may repreatedly take the same number in { x i } i = 1 n \{x_i\}_{i=1}^n {xi​}i=1n​ since it is sampled randomly。

BGD, MBGD和SGD

假设我们想要最小化$J(w)=\mathbb{E}[f(w,X)]$，给定一组来自$X$的随机采样 { x i } i = 1 n \{x_i\}_{i=1}^n {xi​}i=1n​。分别用BGD,SGD,MBGD求解这个问题：

在BGD算法中：

在MBGD算法中：

在SGD算法中

MBGD与BGD和SGD进行比较：

• 与SGD相比，MBGD具有更少的随机性，因为它使用更多的采样数据，而不是像SGD中那样仅仅使用一个。
• 与BGD相比，MBGD在每次迭代中不要求使用全部的samples，这使其更加灵活和高效
• if m=1, MBGD变为SGD
• if m=n, MBGD does NOT become BGD strictly speaking，因为MBGD使用n个样本的随机采样，而BGD使用所有n个样本。特别地，MBGD可能使用 { x i } i = 1 n \{x_i\}_{i=1}^n {xi​}i=1n​中的一个值很多次，而BGD使用每个数值一次。

举个例子：给定一些数值 { x i } i = 1 n \{x_i\}_{i=1}^n {xi​}i=1n​，我们的目标是计算平均值mean: $\bar{x}={\sum }_{i=1}^n{x}_i/n$。这个问题可以等价成一个优化问题：$$\underset{w}{\min }J(w)=\frac{1}{2n}\sum _{i=1}^n||w-w_i|{|}^2$$分别用三个算法求解这个优化问题：

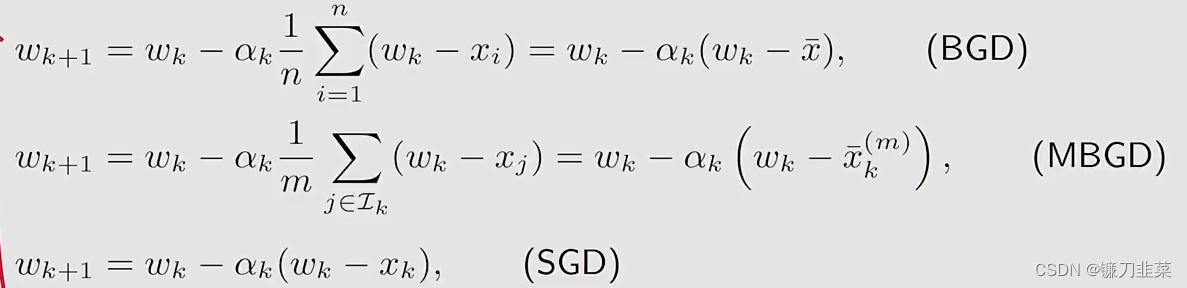
其中${\bar{x}}_k^{(m)}={\sum }_{j\in {\mathcal{L}}_k}{x}_j/m$

更进一步地，如果${\alpha }_k=1/k$，上面等式可以求解为：

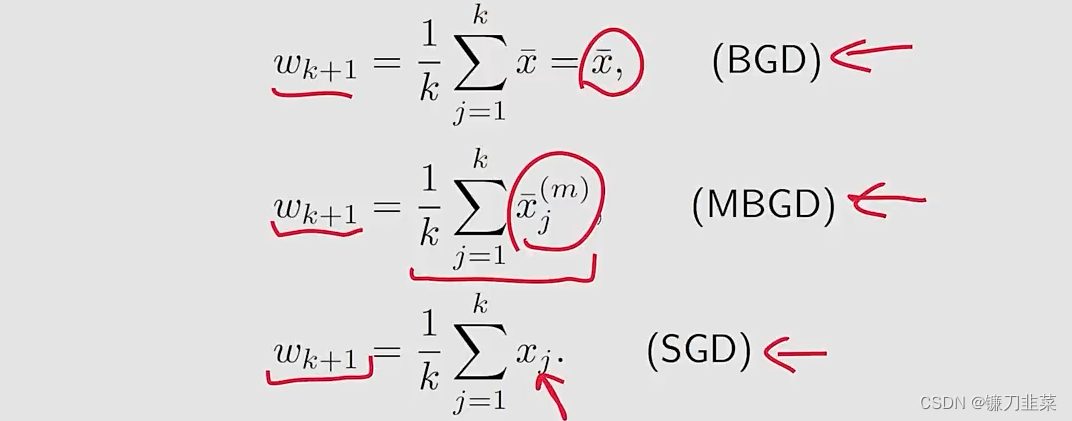
• BGD在每一步的estimate是exactly the optimal solution $w\ast =\bar{x}$
• MBGD的estimate比SGD更快靠近mean，因为${\bar{x}}_k^{(m)}$已经是一个平均。

仿真结果：令${\alpha }_k=1/k$，给定100个点，使用不同的mini-batch size得到不同的收敛速度：

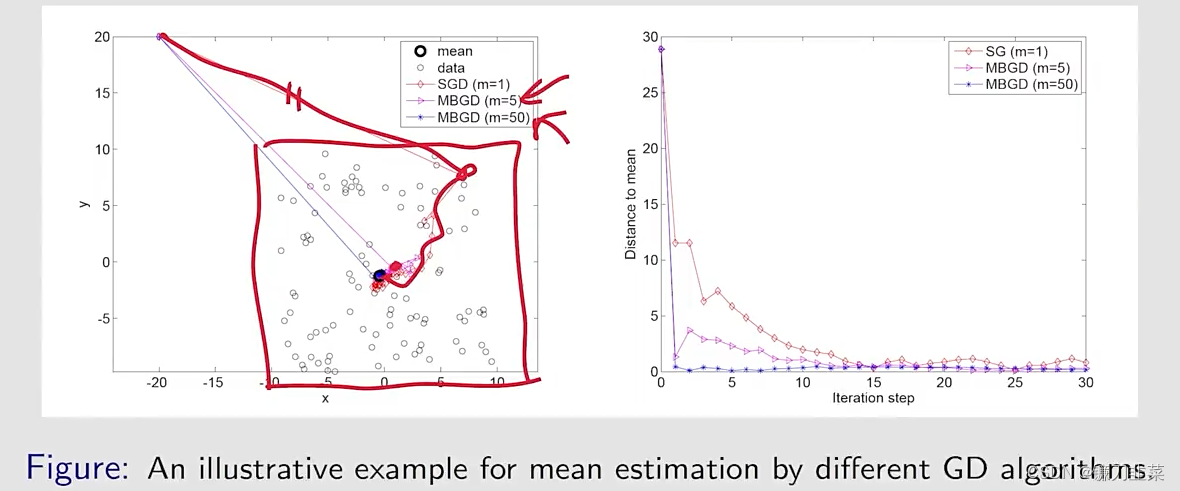
总结

• Mean estimation: 使用 { x k } \{x_k\} {xk​}计算$\mathbb{E}[X]$：$$w_{k+1}=w_k-\frac{1}{k}(w_k-x_k)$$
• RM算法：使用 { g ~ ( w k , η k ) } \{\tilde{g}(w_k,\eta_k)\} {g~​(wk​,ηk​)}求解$g(w)=0$：$$w_{k+1}=w_k-a_k\tilde{g}(w_k,{\eta }_k)$$
• SGD算法：使用 { ∇ w f ( w k , x k ) } \{\nabla_wf(w_k, x_k)\} {∇w​f(wk​,xk​)}最小化$J(w)=\mathbb{E}[f(w,X)]$： $$w_{k+1}=w_k-{\alpha }_k{\nabla }_{w}f(w_k,x_k)$$

内容来源

1. 《强化学习的数学原理》 西湖大学工学院赵世钰教授 主讲
2. 《动手学强化学习》 俞勇 著