理解js的精度问题

news2024/9/20 9:07:04

参考博客：js精度丢失问题-看这篇文章就够了(通俗易懂)、探寻 JavaScript 精度问题以及解决方案、JavaScript 浮点数陷阱及解法

1 为什么

JavaScript 中所有数字包括整数和小数都只有一种类型即 Number类型，它的实现遵循 IEEE 754 标准。

在这里插入图片描述

符号位S：0代表正数，1代表负数
指数位E：存储指数，用来表示次方数
尾数位M：存储尾数，超出的部分自动进1舍0

计算方法：
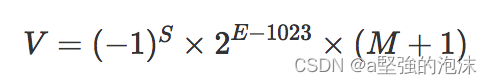
在这里插入图片描述

因为存储时有位数限制（64位），并且某些十进制的浮点数在转换为二进制数时会出现无限循环，会造成二进制的舍入操作(0舍1入)，当再转换为十进制时就造成了计算误差。

了解了存储方法之后，再以0.1来解释一下浮点误差的问题。

将十进制小数 0.1 转为二进制：

0.1 * 2 = 0.2
0.2 * 2 = 0.4 // 循环
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4 // 循环
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
...

可以发现有限十进制小数 0.1 被转化成了无限二进制小数 0.00011001100...（0011循环），表示为科学记数法为1.100110011001100...x2^-4，所以 E=-4+1023=1019，M=100110011...。由于计算机存储的长度又是有限的，所以在一定长度后会进行舍入操作，如图所示，尾数部分存在进位，精度就丢失了。

在这里插入图片描述

再从计算机中取出来的二进制数，是被进位处理过的，转化成十进制后为 0.100000000000000005551115123126，因此就出现了浮点误差。

计算机存储一个27.5的数字

首先把这个数字转换为二进制 11011.1
再把二进制转换为科学记数法 1.10111∗2^4
又因js存储数字用的是双精度浮点数【最多存储64位】即 符号位【1】+指数位【4+1023(固定偏移量)=> 10000000011】+小数部分【10111(52位不够用0补齐)】
即 0100 0000 0011 1011 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

最大安全数的由来：

2位 ===> 2^2=4种组合 ===> 表示的最大十进制整数2^2-1=3

精度位53位 ===> 2^53种组合 ===> 表示的最大十进制整数2^53-1=9007199254740991

能被转化为有限二进制小数的十进制小数的最后一位必然以 5 结尾(因为只有 0.5 * 2 才能变为整数)。所以十进制中一位小数 0.1 ~ 0.9 当中除了 0.5 之外的值在转化成二进制的过程中都丢失了精度。

2 业务场景

场景一：大数危机

比如有个订单号后端定义的是 long 类型，但是当这个订单号转换成 JavaScript 的 Number 类型时候精度会丢失。

preview：

response：

preview中的值是错误的，response中的值是正确的，postman中请求的值跟response是一致的，那说明问题就出现在浏览器中。

查阅资料知道，在preview中，控制台会把发送过来的json数据自动转换成javascript的对象格式，而js的Number类型并不能完全表示Long型的数字，当它超过最大安全数（Math.pow(2, 53) - 1，即 9007199254740991）时，就可能会发生精度丢失的问题。

解决方法：

方案一：在返回数据之前就将数据转换为字符串。
方案二：在传递给 then/catch 前，结合开源库json-bigint，使用transformResponse修改响应数据。

import JSONBig from 'json-bigint';

const res = await axios({
  url: requestUrl,
  params: queryStringParameters,
  data,
  method,
  transformResponse: [
    function (resData) {
      try {
        return JSONBig.parse(resData);
      } catch (e) {
        return JSON.parse(resData);
      }
    },
  ],
});

另外一个情况，如果我门需要使用大于最大安全数的整数，则可以考虑使用BigInt数据类型，它可以表示大于 2^53 - 1 的整数。

9007199254740991+2 // 9007199254740992

9007199254740991n+2n // 9007199254740993n

场景二：浮点数的加减乘除

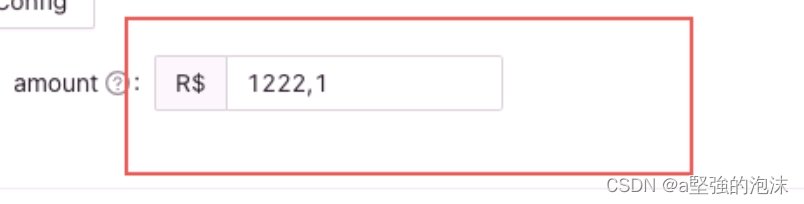
比如涉及费用计算的时候，可能会存在小数相乘的情况。如下图，1222.1*100000应该等于的是122210000，但js乘出来的结果却是122209999.99999999，这也是因为精度丢失导致的。

在这里插入图片描述

解决方法：

方案一：扩大缩小法，将小数转换成字符串，记录小数点后面的位数的长度，再转换成整数相乘，最后除以扩大倍数。

function twoNumberMulti(multiplicand, multiplier) {
  let m = 0;
  const multiplicandStr = String(multiplicand);
  const multiplierStr = String(multiplier);
  if (multiplierStr.includes('.')) {
    m += multiplierStr?.split('.')[1]?.length || 0;
  }
  if (multiplicandStr.includes('.')) {
    m += multiplicandStr?.split('.')[1]?.length || 0;
  }
  return (Number(multiplicandStr.replace('.', '')) * Number(multiplierStr.replace('.', ''))) / 10 ** m;
}

console.log(twoNumberMulti(1222.1,100000)) // 122210000