2022年第十二届MathorCup高校数学建模

C题 自动泊车问题

原题再现

  自动泊车是自动驾驶技术中落地最多的场景之一，自动泊车指在停车场内实现汽车的自动泊车入位过程，在停车空间有限的大城市，是一个比较实用的功能，减少了驾驶员将车辆驶入狭小空间的难度。图 1 为 ApolloD-Kit 车辆在开放露天停车位进行泊车的测试场景，无人车泊入路边一个平行停车位。

  本研究以无人乘用车为例，实现在停车场中进行自动泊车的功能。无人车为阿克曼结构的乘用车，如图 2 所示，前轮转向后轮驱动；车身可以看作一个矩形，长4.9m，宽1.8m；车子轴距2.8m，轮间距为1.7m；最大油门加速度为3.0 m/s!，极限最大减速度为−6.0 m/s!，加加速度不超过20.0 m/s"为宜；方向盘最大转角470°，方向盘与前轮转角的传动比为16: 1（方向盘转动16°，前轮转动1°），方向盘最大转速为400°/s。

  图 3 为某停车场平面图，无人车从初始位置出发，假设以初速度为零开始行驶，将车停在停车场中某一个车位上。停车位上如果没有其他车辆占用，或车位没有被锁，则无人车可停入。停车位有三种类型，分别为垂直停车位（停车方向垂直路面）、平行停车位（停车方向与路面平行）和倾斜停车位。图中用黄色斜线标识的为停车场中部分围墙，白色斜线区域为禁行区域，车辆不能与其产生冲突或碰撞，黄色横线区域为减速带。停车位中的箭头指示为车辆泊车完成后的车头朝向。地面上箭头指示了车辆应该行驶的方向，泊车过程中的倒车方向不予约束。在黄色减速带前后 5m，车辆行驶速度不超过10km/h。

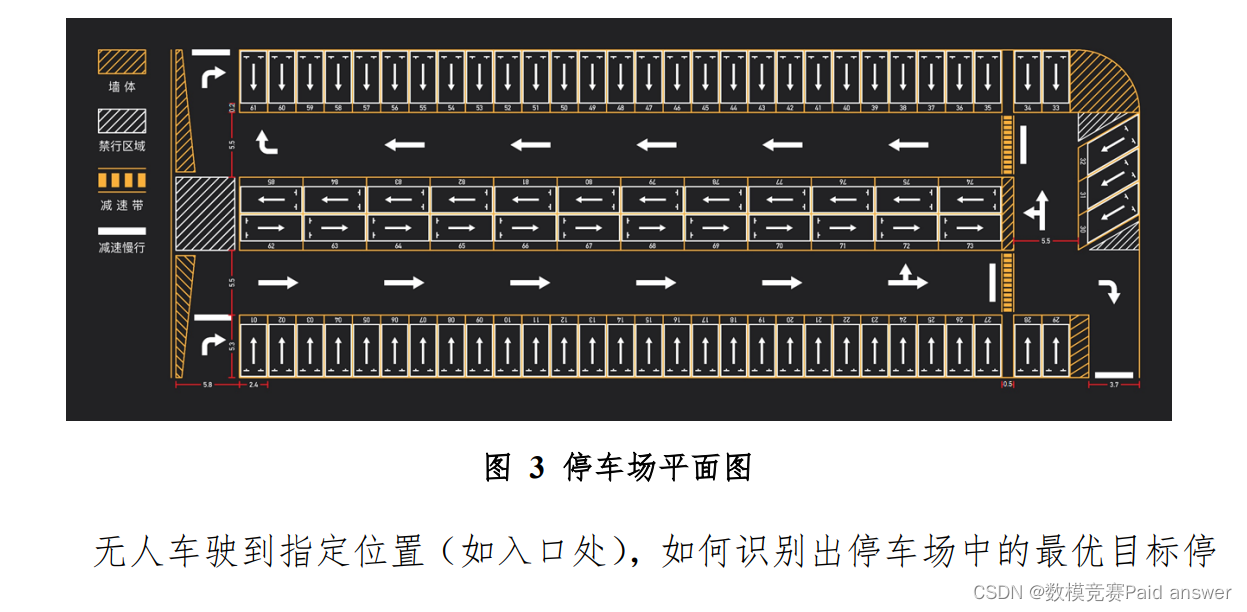
  无人车驶到指定位置（如入口处），如何识别出停车场中的最优目标停车位，以及根据目标车位，如何快速到达并进行安全泊车是自动泊车过程的核心问题。泊车过程在保证安全的情况下，时间应尽可能短，前进车速不超过 20km/h，倒车车速不超过 10km/h，在减速带前后 5m 范围车速不超过 10km/h，轨迹和速度都尽可能平滑（满足最大加速度，最大减速度的约束，并最好满足最大加加速度的约束）。这里轨迹指的是车身中某一特定点的轨迹，即控制点；控制点是事先选定的，通常位于无人车车身对称轴（车身可以近似认为是左右轴对称的）上的一点，在行驶时，控制点的位置会与轨迹点相重合，控制点处的速度方向将与轨迹点的方向角一致，本研究假设控制点位于后轴中心上。请你们的参赛队，研究解决以下问题：
  问题 1： 请根据给出的无人车模型的参数，计算车辆最小转弯半径。如果限制车辆最大加加速度为20 m/s"，无人车沿直线行驶时，最短需要多少距离能加速到最大限制速度20km/h？当车速为20km/h时，无人车如果需要转弯，从沿直线行驶状态开始转弯，路径上的曲率相对路径长度的变化率大小有何限制？
  问题 2：如图 4 所示，无人车初始位置为车库入口，请建立无人车泊车的数学模型，并给出从初始位置到指定停车位的泊车轨迹，轨迹应包括每时刻无人车的行驶路径长度、车辆朝向、速度、加速度、加加速度、角速度、角加速度等，并给出可视化轨迹图。在这个过程中标注红色禁停的停车位都已经被占用，泊车过程中无人车不能与其发生冲突或碰撞。分别考虑三种不同的车位情况，10 号垂直停车位、82 号平行泊车位、31 号倾斜停车位（倾斜角为45°）。

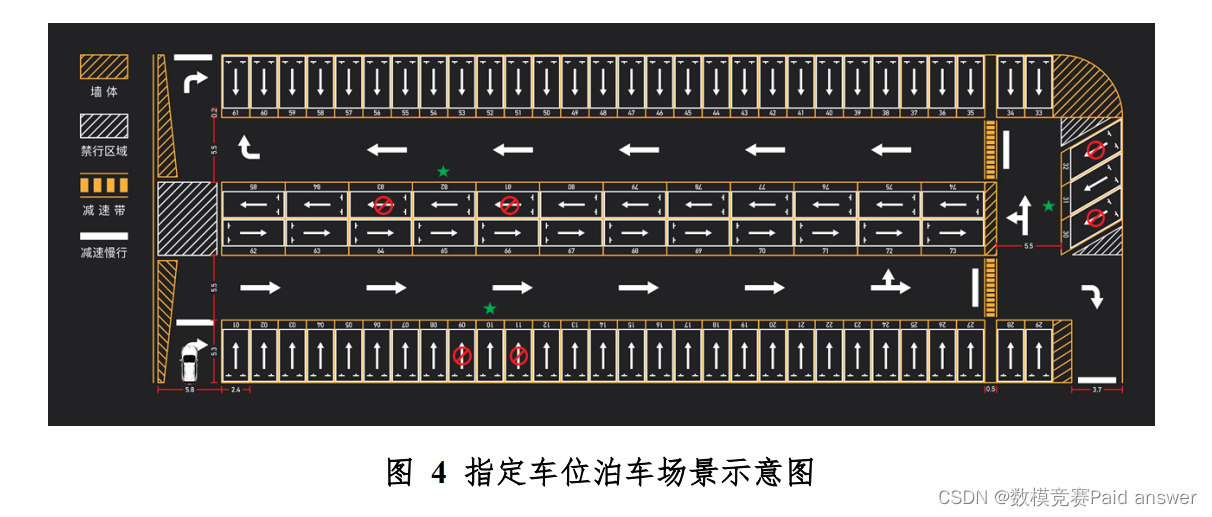
  问题 3：无人车在如图 5 所示的初始位置上，请你们根据当前停车位的状况，建立泊车模型，计算出最优停车位，给出从当前位置到停车位的轨迹；标注红色禁停的停车位都已经被占用，泊车过程中无人车不能与其发生冲突或碰撞。在这个过程中，试建立通用模型，并考虑算法怎样设计能适应车库中任意停车位被占用的状况，并考虑这个过程算法复杂性。

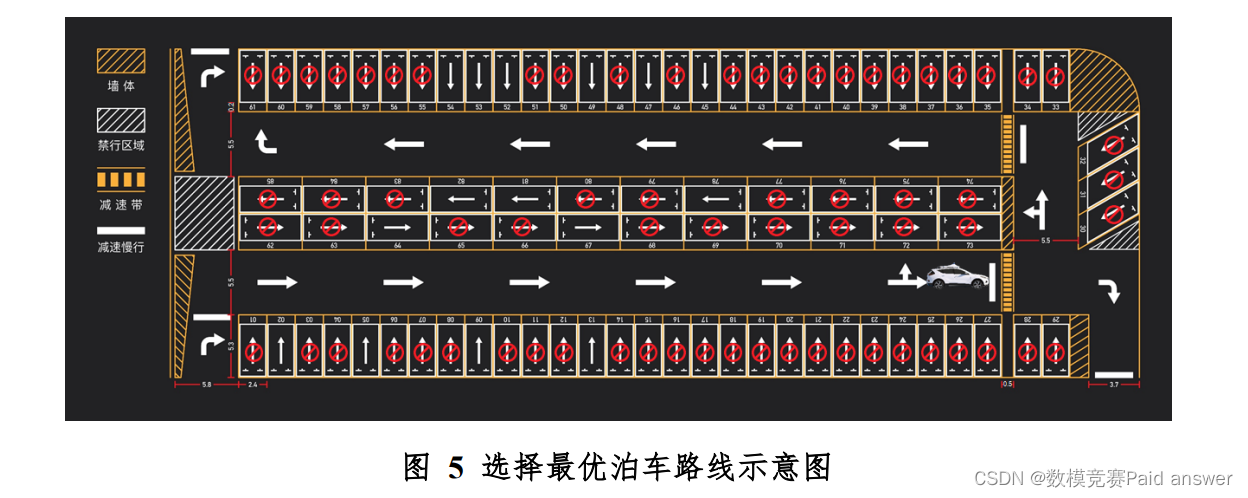
  问题 4：以图 5 为初始状态，假设在当前状态下每小时内从入口进入和从出口离开停车场的车辆均为 30 辆，因车辆的进入和离开，导致停车位会被随机占用或释放。请你们为无人车建立泊车模型，并给出从当前位置到最优停车位的行驶轨迹的仿真结果。

整体求解过程概述(摘要)

  自动泊车系统可以通过车辆周身搭载的传感器测量车身与周围环境之间的距离和角度，收集传感器数据计算出操作流程，同时调整方向盘的转动实现停车入位。因此，自动泊车技术是比较实用的一项功能，自动泊车技术有助于解决人口密集城区的一些停车和交通问题，驾驶者不用再担心因技术不过关而泊不好车。
  本文针对自动泊车问题，主要通过建立 A**模型，应用拟合算法及微分方程参数估计实现三种不同泊车位置下小车行驶路径轨迹的拟合，及对最小的转弯半径和曲率变化率的相关求解。
  针对问题一，我们根据题目中的方向盘最大转角，最大转速等数据来确定控制点位置，计算出前轮的最大转角；通过相关公式可求出最小转弯半径，再通过假设无人车做匀加速直线运动列不等式关系组可求最短路径；最后，通过拟合算法分三部分来讨论曲率相对路径长度的变化率。
  针对问题二，以车库入口为无人车初始位置，基于 A*算法，可以获得无人车从起点到终点的几何路径轨迹；再通过曲线差值法来求出轨迹规划进而求解出位置，速度，加速度及加加速度；最后，再求出角速度及角加速度。
  针对问题三，我们建立了基于蚁群算法的泊车模型。根据停车位的空闲状况，首先规划了合适的泊车轨迹，建立出相应的泊车模型，得到泊车过程中所需的路程及时间。我们以汽车在倒车过程中的旋转角度来辅助我们判断 3 种不同的倒车情况，并以此计算三类情况下所需要的倒车时长，并通过系统的将无人车在直线弯道倒车入库各环节的时间汇总，在已知空余车位的情况下寻求最优解，从而得到整体的停车规划路线，然后对模型进行优化。
  针对问题四，我们依据前三问所求得的数据，建立基于蚁群算法的动态泊车模型。由于车辆的进入和离开，导致停车位会被随机占用或释放，在问题一和问题二中我们可以知道最小转弯半径，曲率变化，各个时刻位置速度等相关参数，根据无人车选择不同的停车位，当可用停车位数量不变情况下，建立数学模型，建立无人车泊车轨迹规划模型，得出无人车泊车策略，并进行仿真实验。

模型假设：

  为了便于考虑问题，我们在不影响模型的准确性的前提下，作出下面的几项假设：
  （1）假设在加速阶段，无人车做匀加速运动，在减速阶段，无人车做匀减速运动；
  （2）假设所有转弯过程车做匀速运动且运动轨迹均为圆弧；
  （3）假设轮胎与地面的摩擦消耗的时间忽略不计；并且忽略无人车在垂直地面的方向上的运动；
  （4）假设无人车不受转向系统相关的影响，直接用前轮转角作为输入；
  （5）忽略车辆受到的空气阻力；车辆与地面保持良好的滚动摩擦；
  （6）假设蚁群算法中只考虑信息素浓度对蚂蚁选择路径的影响。

问题分析：

  针对问题一
  本题主要研究根据给出的无人车模型的数据，计算车辆最小转弯半径，加速到最大限制速度的行驶距离，以及转弯时路径上曲率相对路径长度的变化率大小限制条件。首先，我们根据题目中无人车轴距，轮间距，方向盘最大转角，最大转速等已知数据来确定控制点位置，进一步计算出前轮的最大转角；通过相关公式可求出最小转弯半径，再通过假设无人车做匀加速直线运动列不等式关系组可求最短路径；最后，通过拟合算法分三部分讨论曲率相对路径长度的变化率的影响。
  针对问题二
  本题主要研究了平行泊车系统的路径规划方法，首先根据车辆参数计算出理论可行泊车起始区域；然后分析对比了多种平行泊车路径规划方法的优缺点，最终选取了曲率连续且易于车辆跟踪的等速偏移和正弦曲线的叠加曲线作为此次泊车路径，以车库入口为无人车初始位置，针对车位尺寸较小情况规划了泊车姿态调整，讨论了泊车过程出现障碍物时的路径选取；最后进行了路径仿真分析，验证了路径的可行性。基于 A*算法，可以获得无人车从起点到终点的几何路径；再通过曲线差值法轨迹规划和 Lingo 软件编写程序来求解位置，速度，加速度和加加速度；最后再求角速度和角加速度。
  针对问题三
  本题主要研究了题目需要需要根据停车位现有的状况，建立相应的泊车模型，基于蚁群算法，计算出较优停车位，并得出从当前位置到停车位的轨迹。得到泊车过程中所需时间，首先需要得到整个行驶过程中所需要经过的路段及路段对应的时间，同时需要汽车在倒车过程中的倒车时长，我们以汽车在倒车过程中的旋转角度来确定在不同的倒车情形下，所需要的倒车时长，并通过系统的将无人车在直线弯道倒车入库各环节的时间汇总，在已知空余车位的情况下寻求最优解，从而得到整体的停车规划路线。
   针对问题四
  本题主要研究了每小时内从入口进入和出口离开停车场的车辆均为 30 辆情况下无人车到最优停车位的行驶轨迹，由于车辆的进入和离开，导致停车位会被随机占用或释放，在问题一和问题二中我们可以知道最小转弯半径，曲率变化，各个时刻位置速度等相关参数，根据无人车选择不同的停车位，当可用停车位数量不变情况下，建立数学模型，建立无人车泊车轨迹规划模型，得出无人车泊车策略。现有的基于对路径规划问题的相关的算法研究主要包含 Dijkstra 算法、遗传算法、D** 算法、A** 算法以及粒子群算法等。我们针对实际的停车场环境，进行相关的道路规划，首先对实际的停车场的基本环境进行建模，根据无人车车辆的运动学模型，基于蚁群算法进行路径规划，采用垂直泊车、平行泊车、倾斜泊车三种路径规划方法进行泊车，基本做出车辆安全无碰的泊车入位。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

The actual procedure is shown in the screenshot

clc
clear

mdl_puma560%调出puma560 DH模型作为实验对象
t=[0:0.05:2];%轨迹，步长0.05

T1 = transl(0.4,0.2,0)*trotx(pi);%位移*旋转,创建齐次变换
T2 = transl(0.4,-0.2,0)*trotx(pi/2);

q1 = p560.ikine6s(T1);
q2 = p560.ikine6s(T2);

qq=jtraj(q1,q2,t);%根据各节点，生成轨迹
Tqq=p560.fkine(qq);

qT=p560.jtraj(T1,T2,t);%根据节点矩阵，生成轨迹
Tqt=p560.fkine(qT);

%笛卡尔运动
%笛卡尔空间中直线运动,生成从SE3空间两点间直线的一系列中间位置，结果表达为4*4齐次换矩阵
Ts=ctraj(T1,T2,length(t));
qs=p560.ikine6s(Ts);

figure(1)%绘制各关节角度
for i=1:6
      subplot(2,3,i)
      plot(t, qq(:,i))
      hold on;
      plot(t, qT(:,i))
      plot(t, qs(:,i)) 
      legend('空间-根据各节点规划','节点空间-根据位姿规划','笛卡尔空间')
      hold off;
end

figure(2)
pq=transl(Tqq);%提取旋转矩阵中的位移部分
pT=transl(Tqt);
ps=transl(Ts);
%依次是 '节点空间-根据各节点规划','节点空间-根据节点规划','笛卡尔空间'
subplot(3,1,1)
plot3(pq(:,1),pq(:,2),pq(:,3))
subplot(3,1,2)
plot3(pT(:,1),pT(:,2),pT(:,3))
subplot(3,1,3)
plot3(ps(:,1),ps(:,2),ps(:,3))

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可