2022年数维杯国际大学生数学建模挑战赛
B题 红VS蓝
原题再现:
在现代战争中,攻守双方都需要引入有效的战争策略,以增加战争威胁并减少损失。只有形成相对稳定、平衡的战争态势,才能尽快实现达成共识的最终目标。
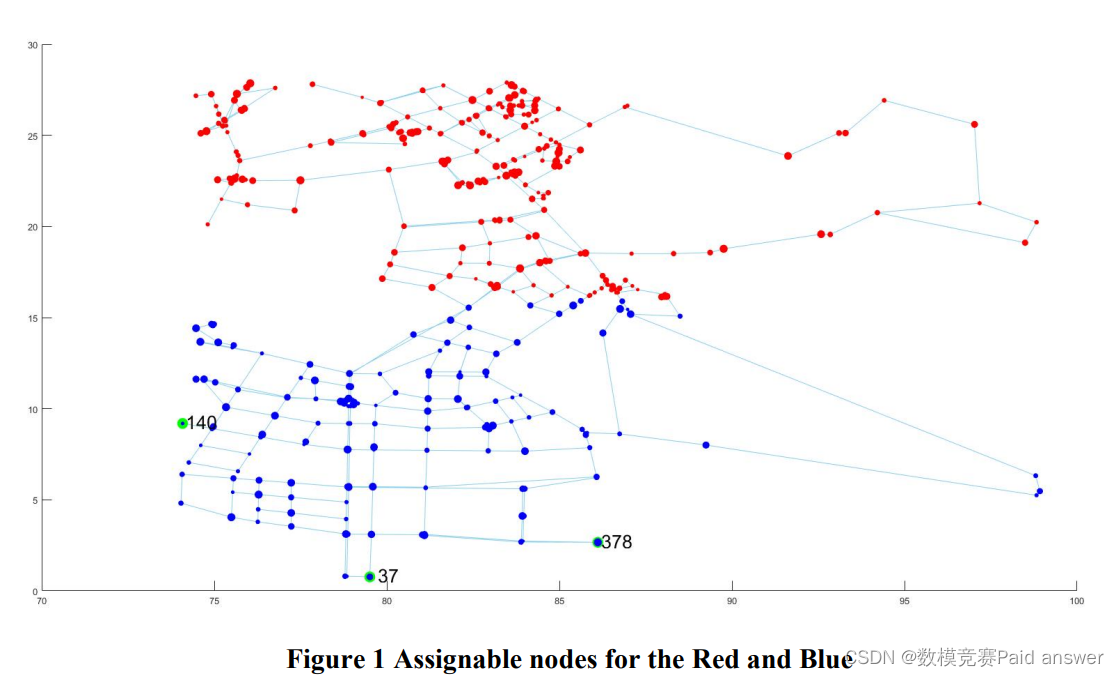
鉴于上述战争问题,请考虑以下对红色VS的简化。蓝战问题:假设红蓝交战如图1所示,双方只能在同色位置进行初始排,每个节点都有自己的攻击难度。攻击难度越大,图1中的圆半径越大,需要根据双方军事武器的实际数量和特点,为每一方提供最优的作战策略。
双方主要作战单位为步兵,主要武器是机动性和隐蔽性的轻型坦克,火力和机动性平衡的中型坦克,重型装甲和强大的火力,具有超远程打击能力和强大火力支援的自行火炮,战略轰炸机(不应部署太多单位以防止轰炸)和高射炮(双方各可设置10个防空点)。红色拥有1万步兵,25架无人机,500辆重型坦克,180辆中型坦克,300辆轻型坦克和420辆自行火炮。蓝色拥有1万步兵,300架无人机,340辆重型坦克,570辆中型坦克,800辆轻型坦克和14000门自行火炮。红色和蓝色武器的具体参数见附件2。请通过适当的简化假设和数学建模方法解决以下三个问题:
问题1:请根据附件1和附件2中的数据,综合考虑各节点的攻击难度、行军距离、武器射程和防空部署,计算出步兵、坦克、自行火炮和防空的分配位置和数量规模双方的火炮,以及双方的最佳指挥位置和几个替代位置。
问题2:基于问题1的优化结果,构建红蓝两边的医疗用品、军需物资和日常物资分配供应的优化模型。同时,在充分考虑对方潜在攻击策略的基础上,在建模过程中提供非供给模式下所需的工人和车辆总数等关键信息。最后,您需要在文本中以表格或图形的形式提供红色和蓝色的最佳供应计划。
问题3:结合前两个问题,在红军进攻和蓝军防守的情况下,请提出红军更好的进攻计划和蓝军更好的撤退计划。鉴于蓝军的撤退节点是[37,140,378],那么在沟通良好和沟通中断的情况下,蓝军的整体撤退计划有哪些不同?
整体求解过程概述(摘要)
在现代战争中,攻守双方都需要引入有效的作战策略,以实现相对稳定和平衡的战争态势,因此各战地的合理布局、弹药的部署和弹药的分配都显得尤为重要。本文分别根据红蓝两侧各节点的攻击难度、行进距离、武器射程和防空部署情况,对这些问题进行了分析研究。
对于问题一,需要计算红蓝两侧步兵、坦克、自行火炮和防空火炮的分配位置和数量大小,以及红蓝两侧的最佳指挥位置和几个备用位置。针对该问题,设置了攻击难度约束、行军距离约束、武器射程和防空部署约束,首先建立动态联合模型,获取红蓝两边步兵、坦克、自行火炮和防空火炮分配位置分布和数量尺度的热图;然后建立以最大攻击难度和最小行进距离为优化目标的位置指挥模型,设计一种免疫求解算法,得到最优指挥位置替代位置的坐标分布位置;
对于问题二,要合理配置医疗物资、军需品和日常物资给红蓝两边,然后考虑到对方存在潜在的攻击策略,根据非补给模式下的劳动力总数和车辆总数给出红蓝双方的最优补给方案。针对该问题,首先将医疗用品、军用物资和日常用品归入弹药类别,通过综合聚类分析联合问题一推导出的最优指挥阵地和替代阵地,然后采用气象无元自动机模型计算待投放物资数量和所需工车总数。
对于问题三,既要提出红方更好的进攻方案,又要提出红方进攻和蓝方防守的更好撤退方案,以及在沟通良好、沟通中断的情况下,分析蓝方整体撤退计划的不同点。针对该问题,首先将问题一和问题二提供的最优作战策略与蚁群算法-路径优化模型相结合,在红攻蓝防守的情况下得到更好的红色进攻解和蓝色更好的撤退解,以及在通信良好的情况下对蓝色的整体撤退解,通信中断在移动距离上有所不同; 在闭关中花费的顺序、路径和时间。
问题分析:
问题背景
自古以来,行军阵型的程度往往是决定刀锋战能否胜的关键。战前,双方要综合考虑兵力、武器数量和质量、地形、物资运输等因素,形成最佳战型,发挥各种武器的优势。然而,现代战争通常是高科技技术下的局部战争。战场形势多变,各种保障结构错综复杂。现代战争中使用的武器杀伤力强,效果广,成本高。
综合这些因素,现代战争双方都需要制定有效的作战战略,在增加战争威胁的同时减少各条战线的损失,只有双方形成更加平衡、稳定、相互支持的作战态势,才能尽快达成共识。俗话说,战争始于人的思想,所以有必要在人的思想中筑起和平的屏障。现代战争的目的不是以武力赢得单方面胜利,而是促进全球长期安全与发展的共同利益。
问题分析
对问题一的分析
对于问题一,根据附件给出的数据,结合红蓝两边各节点的攻击难度、行进距离、武器射程和防空部署,计算双方步兵和武器的分配位置和数量尺度,然后利用免疫优化算法计算出双方的最佳指挥位置和若干备选位置,建立动态联合模型。
对问题二的分析
对于问题二,将医疗用品、军用用品和日常用品归入弹药类别,结合问题1得出的最佳指挥阵地和替代阵地进行综合聚类分析,得出弹药投掷的位置。然后使用元自动机模型来计算要丢弃的物料数量以及所需的工人和车辆总数。
对问题三的分析
对于问题三,将问题一和问题二提供的最优作战策略与蚁群算法-路径优化模型相结合,规划红军最优攻击方案,红军蓝防情况下蓝军最优撤退方案。在沟通良好和沟通中断的情况下,对蓝方的不同撤退计划进行了全面比较。
论文缩略图



全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码
%% 清空环境
clc
clear
%% 算法基本参数
sizepop=100; % 种群规模
overbest=100; % 记忆库容量
MAXGEN=100; % 迭代次数
pcross=0.5; % 交叉概率
pmutation=0.4; % 变异概率
ps=0.95; % 多样性评价参数
length=3; % 选址数
M=sizepop+overbest;
%% step1 识别抗原,将种群信息定义为一个结构体
individuals = struct('fitness',zeros(1,M), 'concentration',zeros(1,M),&ap
os;excellence',zeros(1,M),'chrom',[]);
%% step2 产生初始抗体群
individuals.chrom = popinit(M,length);
trace=[]; %记录每代最个体优适应度和平均适应度
%% 迭代寻优
for iii=1:MAXGEN
%% step3 抗体群多样性评价
for i=1:M
individuals.fitness(i) = fitness(individuals.chrom(i,:)); % 抗 体 与 抗 原 亲 和 度 ( 适 应
度值)计算
individuals.concentration(i) = concentration(i,M,individuals); % 抗体浓度计算
end
% 综合亲和度和浓度评价抗体优秀程度,得出繁殖概率
individuals.excellence = excellence(individuals,M,ps);
% 记录当代最佳个体和种群平均适应度
[best,index] = min(individuals.fitness); % 找出最优适应度
bestchrom = individuals.chrom(index,:); % 找出最优个体
average = mean(individuals.fitness); % 计算平均适应度
trace = [trace;best,average]; % 记录
%% step4 根据 excellence,形成父代群,更新记忆库(加入精英保留策略,可由 s 控制)
bestindividuals = bestselect(individuals,M,overbest); % 更新记忆库
individuals = bestselect(individuals,M,sizepop); % 形成父代群
%% step5 选择,交叉,变异操作,再加入记忆库中抗体,产生新种群
individuals = Select(individuals,sizepop); % 选择
individuals.chrom = Cross(pcross,individuals.chrom,sizepop,length); %
交叉
individuals.chrom = Mutation(pmutation,individuals.chrom,sizepop,length); % 变异
individuals = incorporate(individuals,sizepop,bestindividuals,overbest); %
加入记忆库中抗体
end
%% 画出免疫算法收敛曲线
figure(1)
plot(trace(:,1));
hold on
plot(trace(:,2),'--');
legend('最优适应度值','平均适应度值')
title('免疫算法收敛曲线','fontsize',12)
xlabel('迭代次数','fontsize',12)
ylabel('适应度值','fontsize',12)
%% 画出配送中心选址图
%城市坐标
city_coordinate=[84.001925,7.6674;
83.608775,9.302266667;
83.152275,10.4116;
84.798225,9.813633333;
84.119425,9.5218;
83.0695,9.070433333;
82.9367,7.685733333;
82.9601,8.910266667;
82.897875,9.1235;
82.84975,8.980533333;
82.326175,10.06613333;
74.703175,11.6198;
79.506525,0.7677;
79.5526,3.1024;
79.59225,5.6782;
79.593175,5.719533333;
79.62555,7.734833333;
79.627375,7.858366667;
79.163675,10.28883333;
79.681,10.17963333;
81.184325,9.865066667;
82.311575,10.05843333;
74.0346,4.814966667;
75.49475,4.042833333;
76.261075,3.790233333;
77.230325,3.540033333;
83.96635,4.111366667;
76.284125,5.285033333;
76.27165,4.476233333;
77.228675,4.280233333;
77.22675,5.134366667;
75.5336,5.4157;
78.7876,0.8042;
78.838875,0.800533333;
75.0444,11.47406667;
74.47675,11.63876667;];
carge=[20,90,90,60,70,70,40,90,90,70,60,40,40,40,20,80,90,70,100,50,50,50,80,70,80,40,40,60,70
,50,30];
%找出最近配送点
for i=1:31
distance(i,:)=dist(city_coordinate(i,:),city_coordinate(bestchrom,:)');
end
[a,b]=min(distance');
index=cell(1,length);
for i=1:length
%计算各个派送点的地址
index{i}=find(b==i);
end
figure(2)
title('最优规划派送路线')
cargox=city_coordinate(bestchrom,1);
cargoy=city_coordinate(bestchrom,2);
plot(cargox,cargoy,'rs','LineWidth',2,...
'MarkerEdgeColor','r',...
'MarkerFaceColor','b',...
'MarkerSize',20)
hold on
plot(city_coordinate(:,1),city_coordinate(:,2),'o','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10)
for i=1:31
x=[city_coordinate(i,1),city_coordinate(bestchrom(b(i)),1)];
y=[city_coordinate(i,2),city_coordinate(bestchrom(b(i)),2)];
plot(x,y,'c');hold on
end