数据预处理

非数值类型数据处理

Get_dummies哑变量处理

1. 简单示例：“男”和“女”的数值转换

import pandas as pd
df = pd.DataFrame({'客户编号': [1, 2, 3], '性别': ['男', '女', '男']})
df

	客户编号	性别
0	1	男
1	2	女
2	3	男

df = pd.get_dummies(df, columns=['性别'])
df

	客户编号	性别_女	性别_男
0	1	0	1
1	2	1	0
2	3	0	1

df = df.drop(columns='性别_女') 

df

	客户编号	性别_男
0	1	1
1	2	0
2	3	1

df = df.rename(columns={'性别_男':'性别'})
df

	客户编号	性别
0	1	1
1	2	0
2	3	1

2. 稍复杂点的案例：房屋朝向的数值转换

import pandas as pd
df = pd.DataFrame({'房屋编号': [1, 2, 3, 4, 5], '朝向': ['东', '南', '西', '北', '南']})
df

	房屋编号	朝向
0	1	东
1	2	南
2	3	西
3	4	北
4	5	南

df = pd.get_dummies(df, columns=['朝向'])
df

	房屋编号	朝向_东	朝向_北	朝向_南	朝向_西
0	1	1	0	0	0
1	2	0	0	1	0
2	3	0	0	0	1
3	4	0	1	0	0
4	5	0	0	1	0

df = df.drop(columns='朝向_西') 

df

	房屋编号	朝向_东	朝向_北	朝向_南
0	1	1	0	0
1	2	0	0	1
2	3	0	0	0
3	4	0	1	0
4	5	0	0	1

Label Encoding编号处理

import pandas as pd
df = pd.DataFrame({'编号': [1, 2, 3, 4, 5], '城市': ['北京', '上海', '广州', '深圳', '北京']})

df

	编号	城市
0	1	北京
1	2	上海
2	3	广州
3	4	深圳
4	5	北京

from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
label = le.fit_transform(df['城市'])

print(label)

[1 0 2 3 1]

df

	编号	城市
0	1	北京
1	2	上海
2	3	广州
3	4	深圳
4	5	北京

df['城市'] = label

df

	编号	城市
0	1	1
1	2	0
2	3	2
3	4	3
4	5	1

补充知识点：pandas库中的replace()函数

df = pd.DataFrame({'编号': [1, 2, 3, 4, 5], '城市': ['北京', '上海', '广州', '深圳', '北京']})

df['城市'].value_counts()

北京    2
上海    1
广州    1
深圳    1
Name: 城市, dtype: int64

df['城市'] = df['城市'].replace({'北京': 0, '上海': 1, '广州': 2, '深圳':3})
df

	编号	城市
0	1	0
1	2	1
2	3	2
3	4	3
4	5	0

总结来说，Get_dummies的优点就是它的值只有0和1，缺点是当类别的数量很多时，特征维度会很高，我们可以配合使用下一章即将讲到的PCA主成分分析来减少维度。所以如果Get_dummies类别数目不多时可以优先考虑，其次考虑Label Encoding或replace()函数，但如果是基于树模型的机器学习模型，则是用Label Encoding编号处理则没有太大关系。

重复值、缺失值及异常值处理

重复值处理

# 这里首先创建一个含有重复值的DataFrame，代码如下：
import pandas as pd
data = pd.DataFrame([[1, 2, 3], [1, 2, 3], [4, 5, 6]], columns=['c1', 'c2', 'c3'])

# 此时的data二维列表如下所示，可以看到第一行和第二行是重复的。
data

	c1	c2	c3
0	1	2	3
1	1	2	3
2	4	5	6

# 如果数据量较大，我们可以通过duplicated()函数来查询重复的内容，代码如下：
data[data.duplicated()]

	c1	c2	c3
1	1	2	3

# 如果想统计重复行的数量，可以通过sum()函数进行查看，代码如下，本案例结果为1。
data.duplicated().sum()

1

# 发现有重复行的时候，可以通过drop_duplicates()函数删除重复行，代码如下：
data = data.drop_duplicates()

data

	c1	c2	c3
0	1	2	3
2	4	5	6

# 如果想按列进行去重，比如说如果c1列出现相同的内容，就把那行代码删掉，可以采用如下代码。这样的筛选条件则不如之前要全部一样才删除严格。
data = pd.DataFrame([[1, 2, 3], [1, 2, 3], [4, 5, 6]], columns=['c1', 'c2', 'c3'])
data = data.drop_duplicates('c1')
data

	c1	c2	c3
0	1	2	3
2	4	5	6

缺失值处理

# 这里先构造一个含有缺失值的DataFrame，代码如下：
import numpy as np
data = pd.DataFrame([[1, np.nan, 3], [np.nan, 2, np.nan], [1, np.nan, 0]], columns=['c1', 'c2', 'c3'])
data

	c1	c2	c3
0	1.0	NaN	3.0
1	NaN	2.0	NaN
2	1.0	NaN	0.0

# 可以用isnull()函数或isna()函数（两者作用类似）来查看空值，代码如下：
data.isnull()  # 或者写data.isna()

	c1	c2	c3
0	False	True	False
1	True	False	True
2	False	True	False

# 也可以对单列查看缺失值情况，代码如下：
data['c1'].isnull()

0    False
1     True
2    False
Name: c1, dtype: bool

# 如果数据量较大，可以通过如下代码筛选某列内容为空值的行，代码如下：
data[data['c1'].isnull()]

	c1	c2	c3
1	NaN	2.0	NaN

# 对于空值有两种常见的处理方式：删除空值和填补空值。
# 通过dropna()函数可以删除空值，代码如下：
a = data.dropna()
a

	c1	c2	c3

# 如果觉得该删除方法过于激进，可以设置thresh参数，比如将其设置为n，那么其含义是如果该行的非空值少于n个则删除该行，演示代码如下：
a = data.dropna(thresh=2)
a

	c1	c2	c3
0	1.0	NaN	3.0
2	1.0	NaN	0.0

# 通过finllna()函数可以填补空值，这里采用的是均值填充法，通过每一列的均值对该列的空值进行填充，也可以把其中的data.mean()换成data.meian()则变为中位数填充。
b = data.fillna(data.mean())
b

	c1	c2	c3
0	1.0	2.0	3.0
1	1.0	2.0	1.5
2	1.0	2.0	0.0

# 此处method='pad'代表用缺失值所在列的前一个值填充，如果前一个值不存在或也缺失，则结果不变。运行结果如下：
c = data.fillna(method='pad')
c

	c1	c2	c3
0	1.0	NaN	3.0
1	1.0	2.0	3.0
2	1.0	2.0	0.0

# 还可以采用method='backfill'或method='bfill'用缺失值所在列的后一个值填充，如果后一个值不存在或也缺失，则结果不变。
d = data.fillna(method='backfill')
e = data.fillna(method='bfill')
e

	c1	c2	c3
0	1.0	2.0	3.0
1	1.0	2.0	0.0
2	1.0	NaN	0.0

异常值处理

# 这里先构造一个含有异常值的数据集：
data = pd.DataFrame({'c1': [3, 10, 5, 7, 1, 9, 69], 'c2': [15, 16, 14, 100, 19, 11, 8], 'c3': [20, 15, 18, 21, 120, 27, 29]}, columns=['c1', 'c2', 'c3'])
data

	c1	c2	c3
0	3	15	20
1	10	16	15
2	5	14	18
3	7	100	21
4	1	19	120
5	9	11	27
6	69	8	29

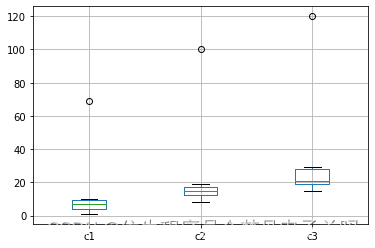
可以看到第一列的数字69，第二列的数字100，第三列的数字120为比较明显的异常值，那么该如何利用Python来进行异常值的检测呢？下面我们主要通过两种方法来进行检测：利用箱体图观察和利用标准差检测。

1. 利用箱型图观察

%matplotlib inline

data.boxplot()  # 画箱型图

<matplotlib.axes._subplots.AxesSubplot at 0x2636e7c2e80>

​

​

2. 利用标准差检测

a = pd.DataFrame()
for i in data.columns:
    z = (data[i] - data[i].mean()) / data[i].std()
    a[i] = abs(z) > 2

a

	c1	c2	c3
0	False	False	False
1	False	False	False
2	False	False	False
3	False	True	False
4	False	False	True
5	False	False	False
6	True	False	False

数据标准化

# 构造数据
import pandas as pd
X = pd.DataFrame({'酒精含量(%)': [50, 60, 40, 80, 90], '苹果酸含量(%)': [2, 1, 1, 3, 2]})
y = [0, 0, 0, 1, 1]

X  # 查看X

	酒精含量(%)	苹果酸含量(%)
0	50	2
1	60	1
2	40	1
3	80	3
4	90	2

min-max标准化

from sklearn.preprocessing import MinMaxScaler
X_new = MinMaxScaler().fit_transform(X)

print(X_new)  # 查看X_new

[[0.2 0.5]
 [0.4 0. ]
 [0.  0. ]
 [0.8 1. ]
 [1.  0.5]]

其中第一列为酒精含量归一化后的值，第二列为苹果酸含量归一化后的值，可以看到它们都属于[0,1]了。在实际应用中，通常将所有数据都归一化后，再进行训练集和测试集划分，演示代码如下：

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_new, y, test_size=0.2, random_state=123)

Z-score标准化

from sklearn.preprocessing import StandardScaler
X_new = StandardScaler().fit_transform(X)

print(X_new)  # 查看X_new

[[-0.75482941  0.26726124]
 [-0.21566555 -1.06904497]
 [-1.29399328 -1.06904497]
 [ 0.86266219  1.60356745]
 [ 1.40182605  0.26726124]]

数据分箱

import pandas as pd
data = pd.DataFrame([[22,1],[25,1],[20,0],[35,0],[32,1],[38,0],[50,0],[46,1]], columns=['年龄', '是否违约'])
data

	年龄	是否违约
0	22	1
1	25	1
2	20	0
3	35	0
4	32	1
5	38	0
6	50	0
7	46	1

# 通过如下代码即可进行等宽数据分箱：
data_cut = pd.cut(data['年龄'], 3)
print(data_cut)

0    (19.97, 30.0]
1    (19.97, 30.0]
2    (19.97, 30.0]
3     (30.0, 40.0]
4     (30.0, 40.0]
5     (30.0, 40.0]
6     (40.0, 50.0]
7     (40.0, 50.0]
Name: 年龄, dtype: category
Categories (3, interval[float64, right]): [(19.97, 30.0] < (30.0, 40.0] < (40.0, 50.0]]

# 通过groupby()函数进行分组，count()函数（详见14.3节补充知识点）进行计数可以获取每个分箱中的样本数目，代码如下：
data['年龄'].groupby(data_cut).count()

年龄
(19.97, 30.0]    3
(30.0, 40.0]     3
(40.0, 50.0]     2
Name: 年龄, dtype: int64

# 补充知识点，分箱并进行编号
print(pd.cut(data['年龄'], 3, labels=[1, 2, 3]))

0    1
1    1
2    1
3    2
4    2
5    2
6    3
7    3
Name: 年龄, dtype: category
Categories (3, int64): [1 < 2 < 3]

WOE值与IV值

WOE值的定义与计算

1. WOE值的定义

2. WOE值的计算过程演示

IV值的定义与计算

1. IV值的定义

2. IV值的计算过程演示

WOE值与IV值的代码实现

1. 数据分箱

# 首先通过如下代码构造数据：
import pandas as pd
data = pd.DataFrame([[22,1],[25,1],[20,0],[35,0],[32,1],[38,0],[50,0],[46,1]], columns=['年龄', '是否违约'])
data

	年龄	是否违约
0	22	1
1	25	1
2	20	0
3	35	0
4	32	1
5	38	0
6	50	0
7	46	1

# 有了数据之后，根据“年龄”这一特征变量进行数据分箱，代码如下：
data_cut = pd.cut(data['年龄'], 3)
data_cut

0    (19.97, 30.0]
1    (19.97, 30.0]
2    (19.97, 30.0]
3     (30.0, 40.0]
4     (30.0, 40.0]
5     (30.0, 40.0]
6     (40.0, 50.0]
7     (40.0, 50.0]
Name: 年龄, dtype: category
Categories (3, interval[float64, right]): [(19.97, 30.0] < (30.0, 40.0] < (40.0, 50.0]]

2. 统计各个分箱样本总数、坏样本数和好样本数

# 统计总客户数
cut_group_all = data['是否违约'].groupby(data_cut).count()
# 统计违约客户
cut_y = data['是否违约'].groupby(data_cut).sum()
# 统计未违约客户
cut_n = cut_group_all - cut_y

# 通过2.2.1节相关知识点将cut_group_all、cut_y、cut_n进行汇总，代码如下，这里我们将违约客户命名为“坏样本”，非违约客户命名为“好样本”。
df = pd.DataFrame()  # 创建一个空DataFrame用来汇总数据
df['总数'] = cut_group_all
df['坏样本'] = cut_y
df['好样本'] = cut_n
df

	总数	坏样本	好样本
年龄
(19.97, 30.0]	3	2	1
(30.0, 40.0]	3	1	2
(40.0, 50.0]	2	1	1

3. 统计各分箱中坏样本比率和好样本比率

# 计算坏样本%和好样本%
df['坏样本%'] = df['坏样本'] / df['坏样本'].sum()
df['好样本%'] = df['好样本'] / df['好样本'].sum()
df

	总数	坏样本	好样本	坏样本%	好样本%
年龄
(19.97, 30.0]	3	2	1	0.50	0.25
(30.0, 40.0]	3	1	2	0.25	0.50
(40.0, 50.0]	2	1	1	0.25	0.25

4. 计算WOE值

import numpy as np
df['WOE'] = np.log(df['坏样本%'] / df['好样本%'])
df

	总数	坏样本	好样本	坏样本%	好样本%	WOE
年龄
(19.97, 30.0]	3	2	1	0.50	0.25	0.693147
(30.0, 40.0]	3	1	2	0.25	0.50	-0.693147
(40.0, 50.0]	2	1	1	0.25	0.25	0.000000

此外，我们在11.5.1节第一部分也讲过，在实际应用中，我们不希望WOE值出现无穷大（这样会导致之后计算的IV值也变为无穷大，丧失了IV值的意义），但是有的时候可能由于数据特殊性及分箱的原因，它还是出现了WOE值为无穷大的情况（某个分箱中只含有一种类别的数据），此时解决办法是当WOE值为无穷大时，将它替换为0，代码如下：

df = df.replace({'WOE': {np.inf: 0, -np.inf: 0}})

df

	总数	坏样本	好样本	坏样本%	好样本%	WOE
年龄
(19.97, 30.0]	3	2	1	0.50	0.25	0.693147
(30.0, 40.0]	3	1	2	0.25	0.50	-0.693147
(40.0, 50.0]	2	1	1	0.25	0.25	0.000000

5. 计算IV值

df['IV'] = df['WOE'] * (df['坏样本%'] - df['好样本%'])
df

	总数	坏样本	好样本	坏样本%	好样本%	WOE	IV
年龄
(19.97, 30.0]	3	2	1	0.50	0.25	0.693147	0.173287
(30.0, 40.0]	3	1	2	0.25	0.50	-0.693147	0.173287
(40.0, 50.0]	2	1	1	0.25	0.25	0.000000	0.000000

iv = df['IV'].sum()
print(iv)

0.34657359027997264

整理上面计算WOE值和IV值的内容，完整代码如下所示：

# 1.构造数据
import pandas as pd
data = pd.DataFrame([[22,1],[25,1],[20,0],[35,0],[32,1],[38,0],[50,0],[46,1]], columns=['年龄', '是否违约'])

# 2.数据分箱
data_cut = pd.cut(data['年龄'], 3)

# 3.统计各个分箱样本总数、坏样本数和好样本数并汇总数据
# 统计总客户数
cut_group_all = data['是否违约'].groupby(data_cut).count()
# 统计违约客户
cut_y = data['是否违约'].groupby(data_cut).sum()
# 统计未违约客户
cut_n = cut_group_all - cut_y
# 汇总基础数据
df = pd.DataFrame()  # 创建一个空DataFrame用来汇总数据
df['总数'] = cut_group_all
df['坏样本'] = cut_y
df['好样本'] = cut_n

# 4.统计坏样本%和好样本%
df['坏样本%'] = df['坏样本'] / df['坏样本'].sum()
df['好样本%'] = df['好样本'] / df['好样本'].sum()

# 5.计算WOE值
import numpy as np
df['WOE'] = np.log(df['坏样本%'] / df['好样本%'])
df = df.replace({'WOE': {np.inf: 0, -np.inf: 0}})  # 替换可能存在的无穷大

# 6.计算各个分箱的IV值
df['IV'] = df['WOE'] * (df['坏样本%'] - df['好样本%'])

# 7.汇总各个分箱的IV值，获得特征变量的IV值
iv = df['IV'].sum()
print(iv)

0.34657359027997264

案例实战：客户流失预警模型的IV值计算

# 将上面的内容首先定义为一个函数
import pandas as pd
import numpy as np

def cal_iv(data, cut_num, feature, target):
    # 1.数据分箱
    data_cut = pd.cut(data[feature], cut_num)

    # 2.统计各个分箱样本总数、坏样本数和好样本数
    cut_group_all = data[target].groupby(data_cut).count()  # 总客户数
    cut_y = data[target].groupby(data_cut).sum()  # 坏样本数
    cut_n = cut_group_all - cut_y  # 好样本数
    # 汇总基础数据
    df = pd.DataFrame()  # 创建一个空DataFrame用来汇总数据
    df['总数'] = cut_group_all
    df['坏样本'] = cut_y
    df['好样本'] = cut_n

    # 3.统计坏样本%和好样本%
    df['坏样本%'] = df['坏样本'] / df['坏样本'].sum()
    df['好样本%'] = df['好样本'] / df['好样本'].sum()

    # 4.计算WOE值
    df['WOE'] = np.log(df['坏样本%'] / df['好样本%'])
    df = df.replace({'WOE': {np.inf: 0, -np.inf: 0}}) 

    # 5.计算各个分箱的IV值
    df['IV'] = df['WOE'] * (df['坏样本%'] - df['好样本%'])

    # 6.汇总各个分箱的IV值，获得特征变量的IV值
    iv = df['IV'].sum()
    
    print(iv)

# 有了上面的自动计算IV值的函数后，通过如下代码来读取客户流失预警模型中的相关数据：
data = pd.read_excel('股票客户流失.xlsx')
data.head()

	账户资金（元）	最后一次交易距今时间（天）	上月交易佣金（元）	本券商使用时长（年）	是否流失
0	22686.5	297	149.25	0	0
1	190055.0	42	284.75	2	0
2	29733.5	233	269.25	0	1
3	185667.5	44	211.50	3	0
4	33648.5	213	353.50	0	1

# 我们利用刚刚编好的函数进行第一个特征变量“账户资金（元）”的IV值计算，代码如下：
cal_iv(data, 4, '账户资金（元）', '是否流失')

0.15205722409339645

for i in data.columns[:-1]:
    print(i + '的IV值为：')
    cal_iv(data, 4, i, '是否流失')  # 调用函数

账户资金（元）的IV值为：
0.15205722409339645
最后一次交易距今时间（天）的IV值为：
0.2508468300174099
上月交易佣金（元）的IV值为：
0.30811632146662304
本券商使用时长（年）的IV值为：
0.6144219248359752

多重共线性的分析与处理

多重共线性的定义

多重共线性的分析与检验

# 使用Pandas库读入一组存在多重共线性的数据，并对其回归作为示例：
import pandas as pd
df = pd.read_excel('数据.xlsx')
df.head()

	X1	X2	X3	Y
0	8	16	-32	77
1	7	14	-31	52
2	4	9	-12	42
3	1	2	5	6
4	1	2	8	19

# 对数据集划分特征变量和目标变量：
X = df.drop(columns='Y')
Y = df['Y']

下面我们需要做的就是分析与检验这三个特征变量是否存在多重共线性，这里主要讲解两种判别方法：相关系数判断以及方差膨胀因子法（VIF检验）来检验多重共线性。

1. 相关系数判断

X.corr()

	X1	X2	X3
X1	1.000000	0.992956	-0.422788
X2	0.992956	1.000000	-0.410412
X3	-0.422788	-0.410412	1.000000

其中第i行第j列的内容表示的就是对应的第i个特征变量和第j个特征变量的相关系数，例如第1行第2列的相关系数：0.99表示的就是特征变量X1和特征变量X2的相关系数，可以看到这两个特征变量的相关性还是非常强的，因此有理由相信这两个变量会导致多重共线性的现象，因此需要删去其中一个特征变量。注意对角线上的相关系数都为1，这个其实没有什么意义，因为它表示的是自身与自身的相关系数，那自然是1了。

2. 方差膨胀因子法（VIF检验）

# 为了检验上述回归中是否存在严重的多重共线性，我们使用Python的VIF检验模块来验证：
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = [variance_inflation_factor(X.values, X.columns.get_loc(i)) for i in X.columns]

vif

[259.6430487184967, 257.6315718292196, 1.302330632715429]

# 如果对上面的快捷写法不太理解，上面的代码也可以写成：
vif = []
for i in X.columns:  # i对应的是每一列的列名
    vif.append(variance_inflation_factor(X.values, X.columns.get_loc(i)))
    
vif

[259.6430487184967, 257.6315718292196, 1.302330632715429]

# 对数据集重新划分特征变量和目标变量：
X = df[['X1', 'X3']]
Y = df['Y']

# 进行检验VIF检验：
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = [variance_inflation_factor(X.values, X.columns.get_loc(i)) for i in X.columns]

vif

[1.289349054516766, 1.289349054516766]

过采样和欠采样

过采样

1. 过采样的原理

(1) 随机过采样

(2) SMOTE法过采样

2. 过采样的代码实现

import pandas as pd
data = pd.read_excel("信用卡数据.xlsx")
data.head()

	编号	年龄	负债比率	月收入	贷款数量	家属人数	分类
0	1	29	0.22	7800	1	3	0
1	2	52	0.46	4650	1	0	0
2	3	28	0.10	3000	0	0	0
3	4	29	0.20	5916	0	0	0
4	5	27	1.28	1300	0	0	1

# 通过如下代码提取特征变量并将其赋值给变量X，提取目标变量并将其赋值给变量y：。
X = data.drop(columns='分类')
y = data['分类']

# 然后使用collections库中的Counter()方法，对目标变量进行计数：
from collections import Counter
Counter(y)

Counter({0: 1000, 1: 100})

不违约的样本数有1000个，远远大于违约的样本数100。为了防止建立信用违约模型时，模型着重拟合不违约的样本，而无法找出违约的样本，我们采用过采样的方法来改善样本比例不均衡的问题，这里我们将通过上面讲到的随机过采样和SMOTE法过采样来进行代码实现。

（1）随机过采样

from imblearn.over_sampling import RandomOverSampler
ros = RandomOverSampler(random_state=0)
X_oversampled, y_oversampled = ros.fit_resample(X, y)

# 用Counter()方法检验一下SMOTE过采样的效果。
Counter(y_oversampled)

Counter({0: 1000, 1: 1000})

违约的样本数从100上升至不违约的样本数1000，这证明我们的随机过采样有效。同时我们可以打印特征变量X_oversampled的shape来看看特征变量的变化：

X_oversampled.shape

(2000, 6)

这里的2000就是1000个违约样本和1000个不违约样本相加得到的，可以看到，随机过采样后特征变量的数据也随之增多。

（2）SMOTE过采样

# 通过如下代码即可进行SMOTE过采样：
from imblearn.over_sampling import SMOTE
smote = SMOTE(random_state=0)
X_smotesampled, y_smotesampled = smote.fit_resample(X, y)

# 用Counter()方法检验一下SMOTE过采样的效果。
Counter(y_smotesampled)

Counter({0: 1000, 1: 1000})

欠采样

1. 欠采样的原理

2. 欠采样的代码实现

# 仍然采用上方的信用违约数据进行欠采样代码的展示：
from imblearn.under_sampling import RandomUnderSampler
rus = RandomUnderSampler(random_state=0)
X_undersampled, y_undersampled = rus.fit_resample(X, y)

# 用Counter()方法检验一下随机欠采样的效果。
Counter(y_undersampled)

Counter({0: 100, 1: 100})

# 不违约的样本数从1000下降至违约的样本数100，这证明我们的随机欠采样有效。同时我们可以打印特征变量X_undersampled的shape来看看特征变量的变化：
X_undersampled.shape

(200, 6)