文章目录
- 前言
- 一、移动零(力扣283)【双指针】
- 二、轮转数组(力扣189)
- 三、寻找数组的中心下标(力扣728)
- 四、和为 K 的子数组(力扣560)
- 五、按奇偶排序数组 II(力扣922)【双指针】
- 六、爱吃香蕉的珂珂(力扣875)【二分法】
- 每日一题:按位与为零的三元组(力扣982)
- 每日一题:经营摩天轮的最大利润(力扣1599)
前言
1、移动零
2、轮转数组
3、寻找数组的中心下标
4、和为 K 的子数组
5、按奇偶排序数组||
6、爱吃香蕉的珂珂
一、移动零(力扣283)【双指针】
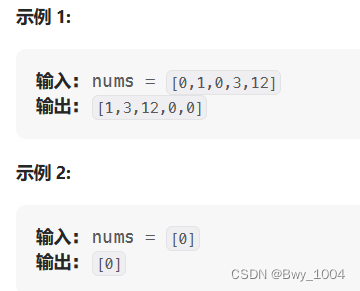
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
class Solution {
public void moveZeroes(int[] nums) {
int slowIndex =0;
int fastIndex = 0;
for(;fastIndex<nums.length;fastIndex++){
if(nums[fastIndex]!=0){
nums[slowIndex++]=nums[fastIndex];
}
}
//剩下的补零
for(int i=slowIndex;i<nums.length;i++){
nums[i] = 0;
}
}
}
二、轮转数组(力扣189)
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
最简单的想法 开辟一个新的数组暂时存放元素 空间复杂度为O(n)
还要注意一点:本题还有一个小陷阱,题目输入中,如果k大于nums.length了应该怎么办? ------>取模运算
class Solution {
public void rotate(int[] nums, int k) {
int Index =0;
int length = nums.length;
int moveTme = k%length;
int[] temp = new int[moveTme];
if(nums.length==1) return ;
for(int i=length-moveTme;i<length;i++){
temp[Index++] = nums[i];
}
int fastIndex = length-1;
for(int i=length-moveTme-1;i>=0;i--){
nums[fastIndex--] = nums[i];
}
int slowIndex = 0;
for(int i=0;i<=fastIndex;i++){
nums[slowIndex++] = temp[i];
}
}
}
方法二:翻转数组
第一步:把整个数组进行翻转
第二步:分为两部分:【0:k-1】 【k:nums.length-1】分别一次翻转即可
class Solution {
public void rotate(int[] nums, int k) {
//翻转数组
int moveTime = k%nums.length;
reverse(nums,0,nums.length-1);
reverse(nums,0,moveTime-1);
reverse(nums,moveTime,nums.length-1);
}
public void reverse(int[] nums,int start,int end){
while(start<end){
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start+=1;
end-=1;
}
}
}
三、寻找数组的中心下标(力扣728)
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。

一开始会想到双指针,但是需要修补很多边边角角,较为繁琐
左求和*2+中心索引值 = 总和
class Solution {
public int pivotIndex(int[] nums) {
int sum =0;
for(int i=0;i<nums.length;i++){
sum+=nums[i];
}
int left =0;
int right=0;
for(int i=0;i<nums.length;i++){
sum -=nums[i];
if(sum==left) return i;
left += nums[i];
}
return -1;
}
}
四、和为 K 的子数组(力扣560)
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。

分析:
第一感觉是滑动窗口,但是在试了很久之后发现并不可行。
为什么这题不可以用双指针/滑动窗口:因为nums[i]可以小于0,也就是说右指针i向后移1位不能保证区间会增大,左指针j向后移1位也不能保证区间和会减小。给定j,i的位置没有二段性,vice versa(反之亦然)。
暴力求解:
public class Solution {
public int subarraySum(int[] nums, int k) {
int count = 0;
for (int start = 0; start < nums.length; ++start) {
int sum = 0;
for (int end = start; end >= 0; --end) {
sum += nums[end];
if (sum == k) {
count++;
}
}
}
return count;
}
}
前缀和+哈希表
基于方法一利用数据结构进行进一步的优化

五、按奇偶排序数组 II(力扣922)【双指针】
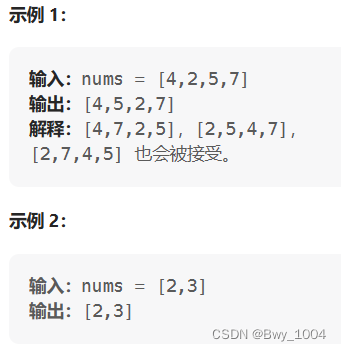
给定一个非负整数数组 nums, nums 中一半整数是 奇数 ,一半整数是 偶数 。
对数组进行排序,以便当 nums[i] 为奇数时,i 也是 奇数 ;当 nums[i] 为偶数时, i 也是 偶数 。
你可以返回 任何满足上述条件的数组作为答案 。
class Solution {
public int[] sortArrayByParityII(int[] nums) {
int jishuIndex = nums.length-1;
int oushuIndex = 0;
while(jishuIndex>0 && oushuIndex<nums.length-1){
while(jishuIndex>0 && nums[jishuIndex]%2==1){
jishuIndex-=2;
}
while(oushuIndex<nums.length-1 && nums[oushuIndex]%2==0){
oushuIndex+=2;
}
//交换元素:
if(jishuIndex>0 && oushuIndex<nums.length-1){
int temp = nums[oushuIndex];
nums[oushuIndex] = nums[jishuIndex];
nums[jishuIndex] = temp;
oushuIndex+=2;
jishuIndex-=2;
}
}
return nums;
}
}
六、爱吃香蕉的珂珂(力扣875)【二分法】
珂珂喜欢吃香蕉。这里有 n 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 h 小时后回来。
珂珂可以决定她吃香蕉的速度 k (单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉 k 根。如果这堆香蕉少于 k 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 h 小时内吃掉所有香蕉的最小速度 k(k 为整数)。

分析:
珂珂可以一小时吃一根香蕉 也可以一小时吃两根香蕉,最多一小时可以吃香蕉堆的最大值,速度可以一直增加,增加速度太慢,所以使用二分法增加
class Solution {
public int minEatingSpeed(int[] piles, int h) {
int maxBanana = 0;
//先找到二分查找的边界值
for(int i=0;i<piles.length;i++){
if(piles[i]>maxBanana){
maxBanana = piles[i];
}
}
int left = 1;
int mid = 0;
int k = maxBanana;
while(left<maxBanana){
mid = (left+maxBanana)/2;
//二分法 把此时的速度传进去,看看需要多长时间 比h大还是小
long res = checkEat(mid,piles);
if(res>h){
//k应该增加;
left=mid+1;
}else{
maxBanana = mid;
k=mid;
}
}
return k;
}
public long checkEat(int speed,int[] piles){
long time = 0;
for(int i=0;i<piles.length;i++){
if(piles[i]<speed){
time++;
}else{
int h = piles[i]/speed;
if(piles[i]%speed==0){
time+=h;
}else time+=(h+1);
}
}
return time;
}
}
每日一题:按位与为零的三元组(力扣982)
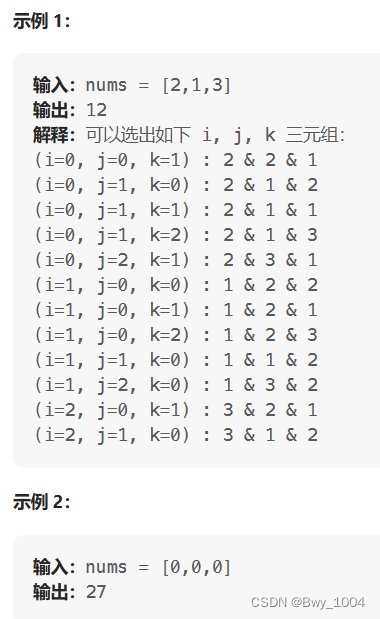
给你一个整数数组 nums ,返回其中 按位与三元组 的数目。
按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件:
0 <= i < nums.length
0 <= j < nums.length
0 <= k < nums.length
class Solution {
public int countTriplets(int[] nums) {
int[] map = new int[1<<16];
int count = 0;
//nums[i] 和 nums[j]的结果
for(int x:nums){
for(int y:nums){
++map[x & y];
}
}
for(int x:nums){
for(int y=0;y<1<<16;y++){
if((x&y)==0){
count += map[y];
}
}
}
return count;
}
}
每日一题:经营摩天轮的最大利润(力扣1599)
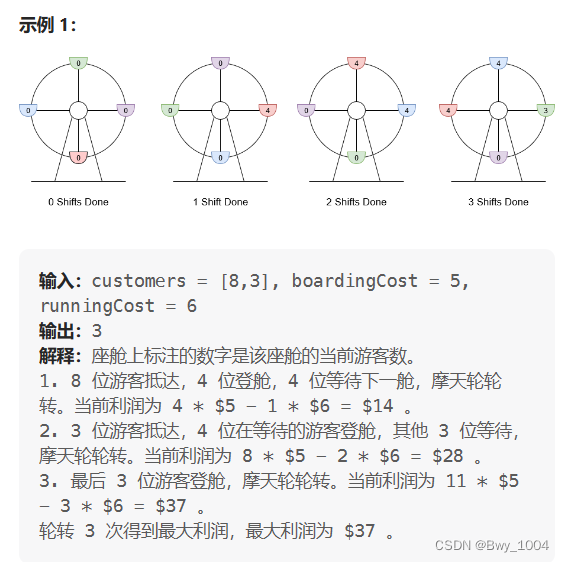
正在经营一座摩天轮,该摩天轮共有 4 个座舱 ,每个座舱 最多可以容纳 4 位游客 。你可以 逆时针 轮转座舱,但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。
给你一个长度为 n 的数组 customers , customers[i] 是在第 i 次轮转(下标从 0 开始)之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ,一旦该座舱再次抵达地面,他们就会离开座舱结束游玩。
你可以随时停下摩天轮,即便是 在服务所有游客之前 。如果你决定停止运营摩天轮,为了保证所有游客安全着陆,将免费进行所有后续轮转 。注意,如果有超过 4 位游客在等摩天轮,那么只有 4 位游客可以登上摩天轮,其余的需要等待 下一次轮转 。
返回最大化利润所需执行的 最小轮转次数 。 如果不存在利润为正的方案,则返回 -1 。
题目太费解。重新描述一下,为"最佳跑路时机"。 迪士尼把它的摩天轮游乐场卖给你了,约好明天付款,今天你先试运行一下。但你其实没有那么多钱,今天必须跑路。 摩天轮不能停,从早上开门就必须一直按固定的速率旋转。 电力公司不信任你,每旋转一格,电力公司就实时从你的账中划走一笔电费runningCost。 你有未卜先知的能力,知道每个时刻,达到的顾客数目有多少。而且这些顾客都是死忠,坐不上摩天轮就不走。 每个顾客在坐上去的同时,扫码转账给你boardingCost。 问:你什么时候拉闸跑路,钱最多?天上的顾客等救援机构来了再说。。。
class Solution {
public int minOperationsMaxProfit(int[] customers, int boardingCost, int runningCost) {
int wait =0;
int person=0;
int maxProfit = 0;
int res = -1;
int profit =0;
//首先肯定需要遍历顾客数量
for(int i=0;i<customers.length || person>0;i++){
if(i<customers.length){
person += customers[i];
}
profit += Math.min(person,4)* boardingCost-runningCost;
person-=Math.min(person,4);
if(profit>maxProfit){
maxProfit = profit;
res = i+1;
}
}
return res;
}
}