在看西瓜书的时候有些地方的数学推导（尤其是概率论的似然、各种分布）让我很懵逼，本科的忘光了，感觉有点懂又不太懂，基于此，干脆花一点时间简单从头归纳一下机器学习中的数学基础，也就是高数、线代、概率论（其实大学都学过）。
本文全部都是基于我自己的数学基础、尽量用方便理解的文字写的，记录的内容都是我本人记忆不太牢靠、需要时常来翻笔记复习的知识，已经完全掌握的比如极限连续性啥的都不会出现在这里。

学习内容来自这里

2 线代

2.1 矩阵

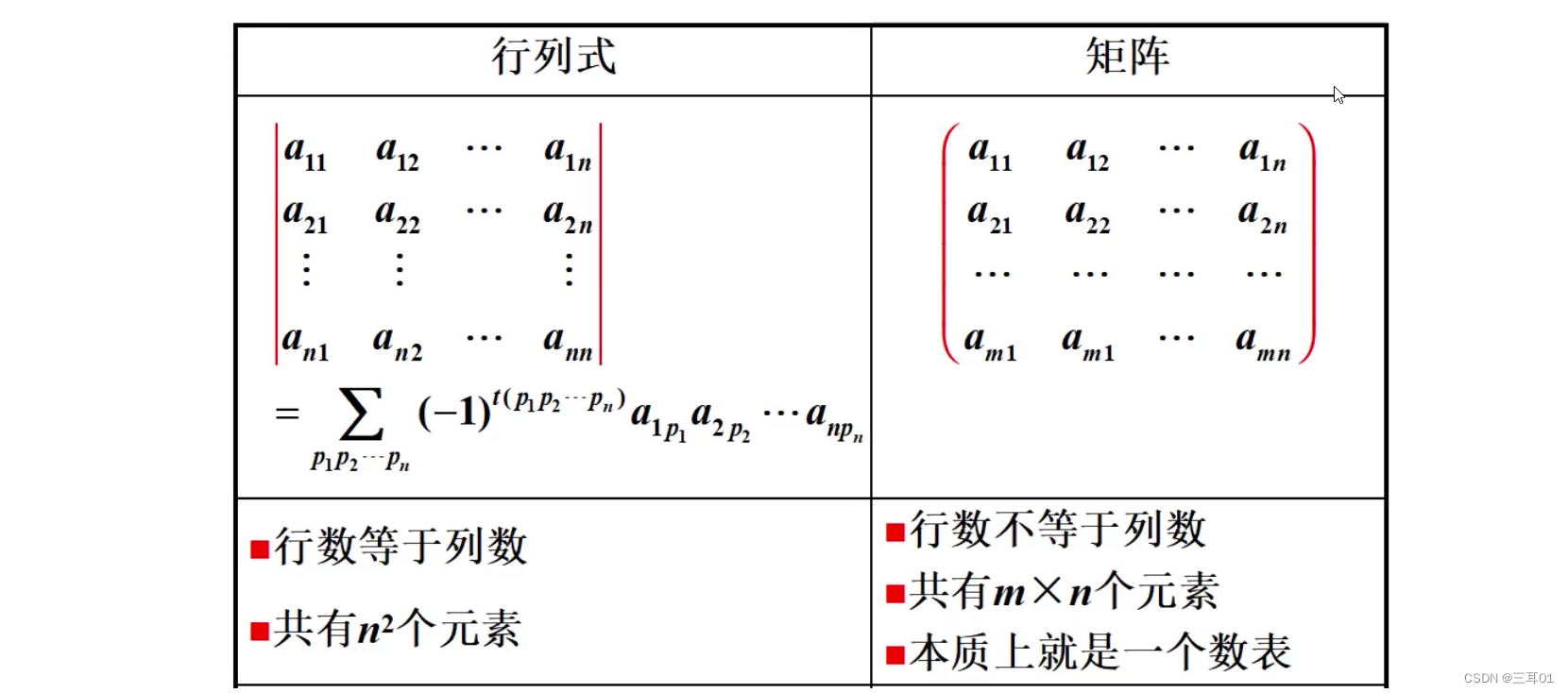
矩阵就是数据，对数据做任何操作都是对矩阵做操作。
行=列就是方阵。

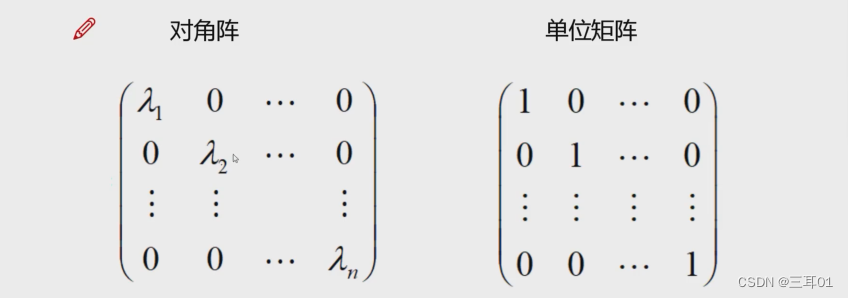
同型矩阵：行、列相同。

2.2 矩阵的秩

秩就是矩阵有几个极大线性无关组。
行的秩=列的秩。

理解：

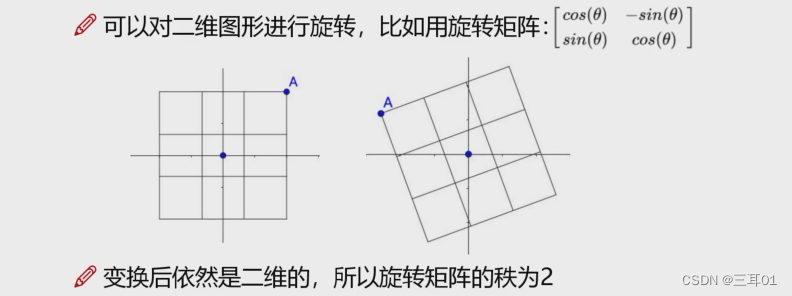
比如图中第一张图点A的坐标是(x,y)，经过旋转矩阵之后，变成了：
$$[xcos\theta +ysin\theta ,-xsin\theta +ycos\theta ]$$原来是二维图形，经过旋转矩阵之后，仍然是二维图形，所以旋转矩阵的秩=2。
这一点在图像也可以直观地看出来：旋转矩阵无法线性组合。

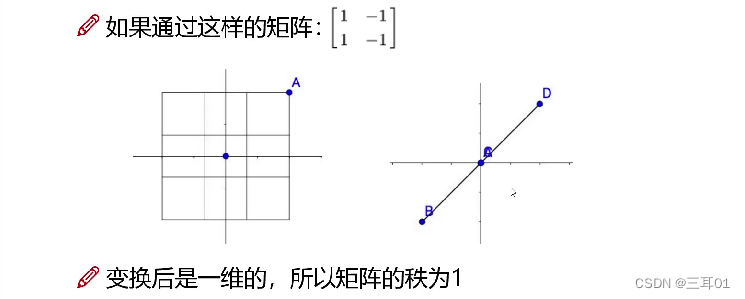
矩阵中最大不相关向量的个数就是秩。

2.3 内积与正交

内积=0，则向量正交：

2.4 特征值与特征向量

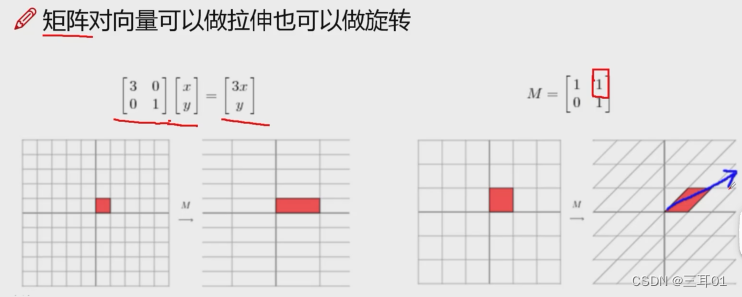
如图所示，对角矩阵表示对向量拉伸，如果在其它位置上有值，那就有旋转操作。

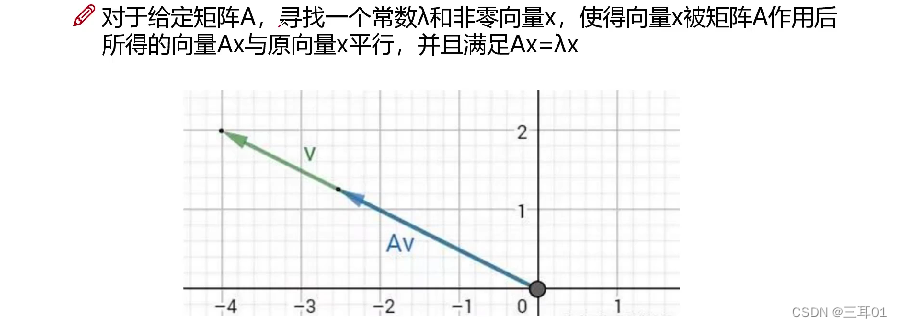
x是特征向量，$\lambda$是特征值。特征值与特征向量是矩阵中信息描述的主要工具。
普遍可以这样认为：特征向量代表方向，特征值代表这个方向的重要程度。特征值大，就是主要信息。
特征空间包含了所有的特征向量。

应用：
图像就是 长×宽×通道数 的矩阵，所以可以通过特征值，提取主要信息。这就是图像压缩。

特征值和特征向量是为了研究向量在经过线性变换后的方向不变性而提出的：
1）一个矩阵和该矩阵的非特征向量相乘是对该向量的旋转变换；
2）一个矩阵和该矩阵的特征向量相乘是对该向量的伸缩变换，其中伸缩程度取决于特征值大小
矩阵在特征向量所指的方向上具有 增强（或减弱）特征向量 的作用。这也就是说，如果矩阵持续地叠代作用于向量，那么特征向量的就会突显出来。

2.5 SVD矩阵分解

2.5.1 要解决的问题

问题：数据过大且稀疏。
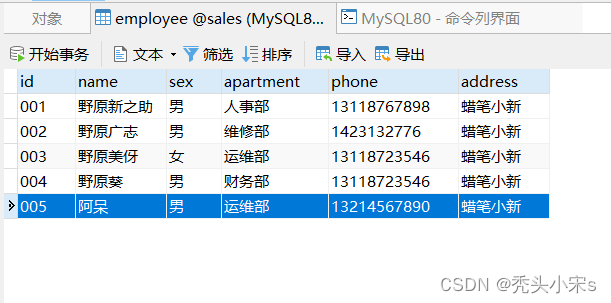
举例：以电商数据为例，如果有100万个客户，供选择的商品有10万个，那么这就是一个 100万×10万 的矩阵，这个数据量未免过于庞大，而且每一个客户可能只在这些商品中选择寥寥几种，所以这个矩阵会非常稀疏。那么就可以把它分解成一个 100万×10 的矩阵和一个 10×10万 的矩阵，前者表示客户，后者表示商品，这就是SVD矩阵分解要解决的问题。

2.5.2 基变换

什么是基？

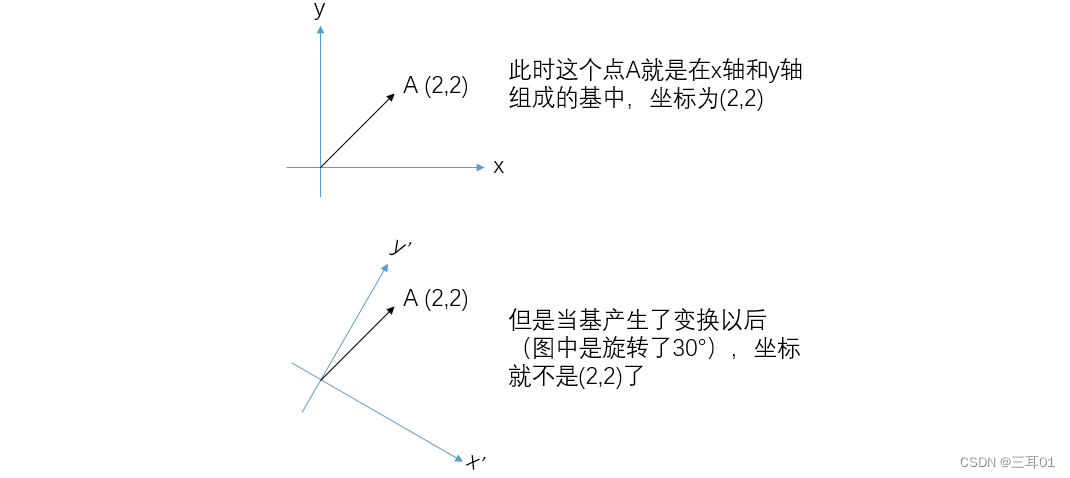
要计算的话，就是直接把原坐标与新的基相乘（矩阵乘法本质是一种变换，是把一个向量，通过旋转，拉伸，变成另一个向量的过程）：

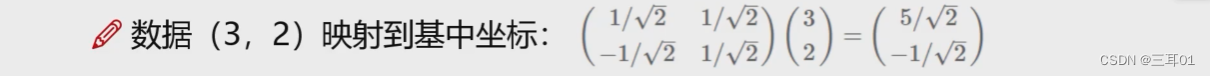
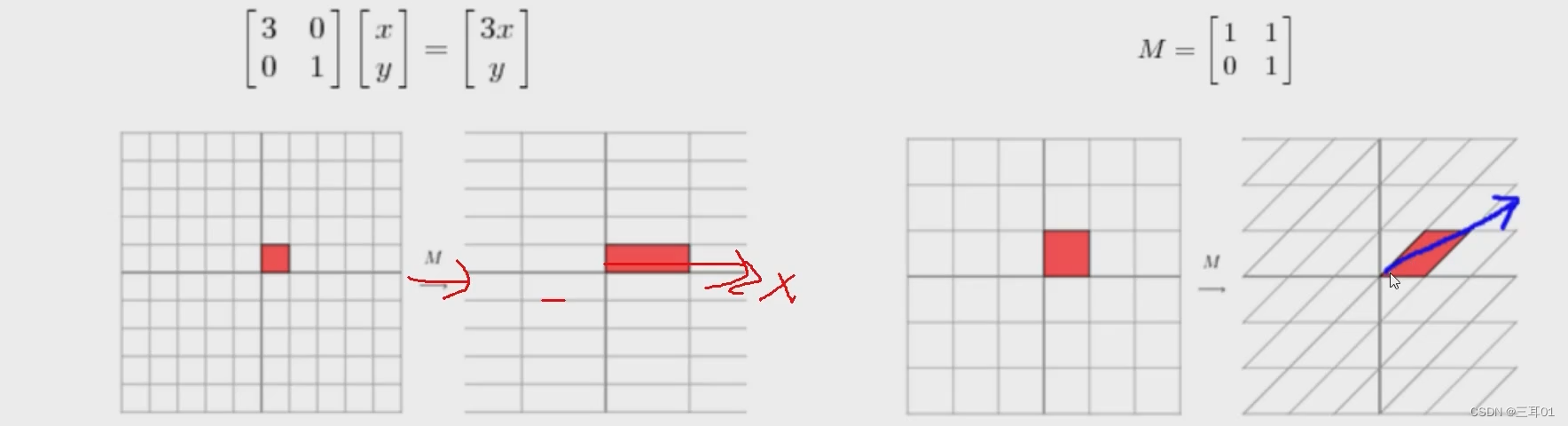
从下面这张图可以看到：左边是进行了x轴的拉伸，右边是有一个旋转。
所以左边的主要方向就是x轴，右边的主要方向就是图中箭头部分。

2.5.3 特征值分解

特征值分解是矩阵分解的一种方法，矩阵分解也称为矩阵因子分解，即将原始矩阵表示成新的结构简单或者具有特殊性质的两个或多个矩阵的乘积，类似于代数中的因子分解。

特征值分解的实质是求解给定矩阵的特征值和特征向盘，提取出矩阵最重要的特征，特征值分解公式：$$A=V\Lambda V^{-1}$$其中V为特征向量矩阵， $\Lambda$是特征值对角阵。

为什么是这样？
因为前面提过：

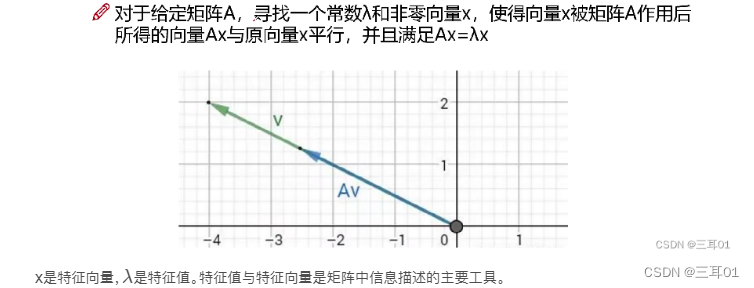
x是运动方向，$\lambda$是运动速度。
这个式子是不完备的，对于一个秩为m的矩阵 ，应该存在m个这样的式子，完备式子应该是：$AX=X\Lambda$，所以特征值分解公式就是$A=X\Lambda X^{-1}$。

基的要求：正交，即线性无关

缺陷：
特征值分解仅适用于提取方阵特征，但在实际应用中，大部分数据对应的矩阵都不是方阵；
矩阵可能是有很多0的稀疏矩阵，存储量大且浪费空间，这时就需要提取主要特征。

2.5.4 奇异值分解（SVD）

SVD是将任意较复杂的矩阵用更小、更简单的 3个子矩阵的相乘表示 ，用这3个小矩阵来描述大矩阵重要的特性。

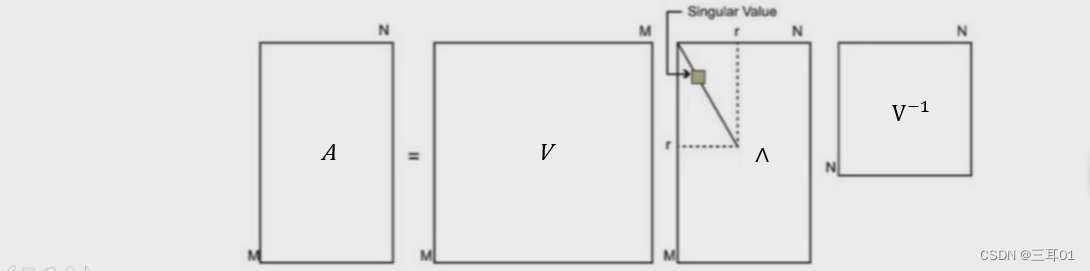
但是可以看到这三个分解出来的矩阵反而都很大。
所以只要提取特征向量里面的主要信息就可以了，比如这里我们提取k个主要信息，则中间的矩阵就变成了$k\times k$了：

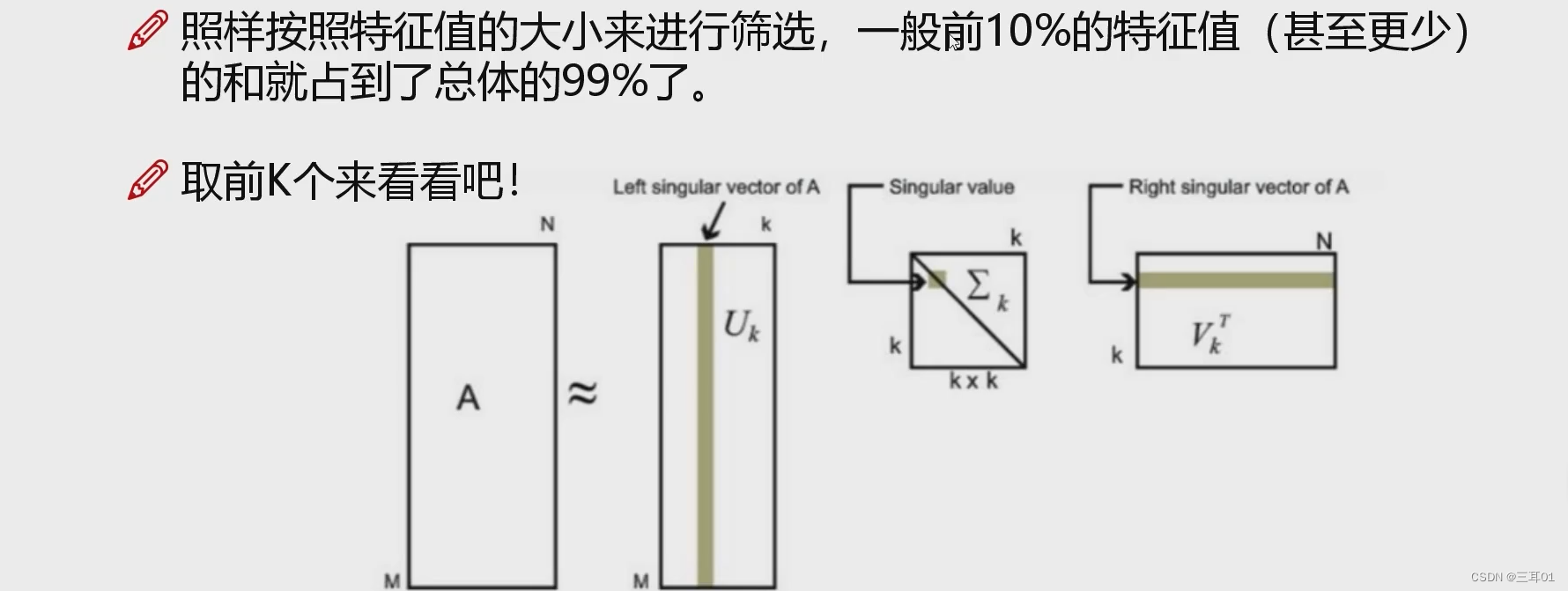
SVD推导：

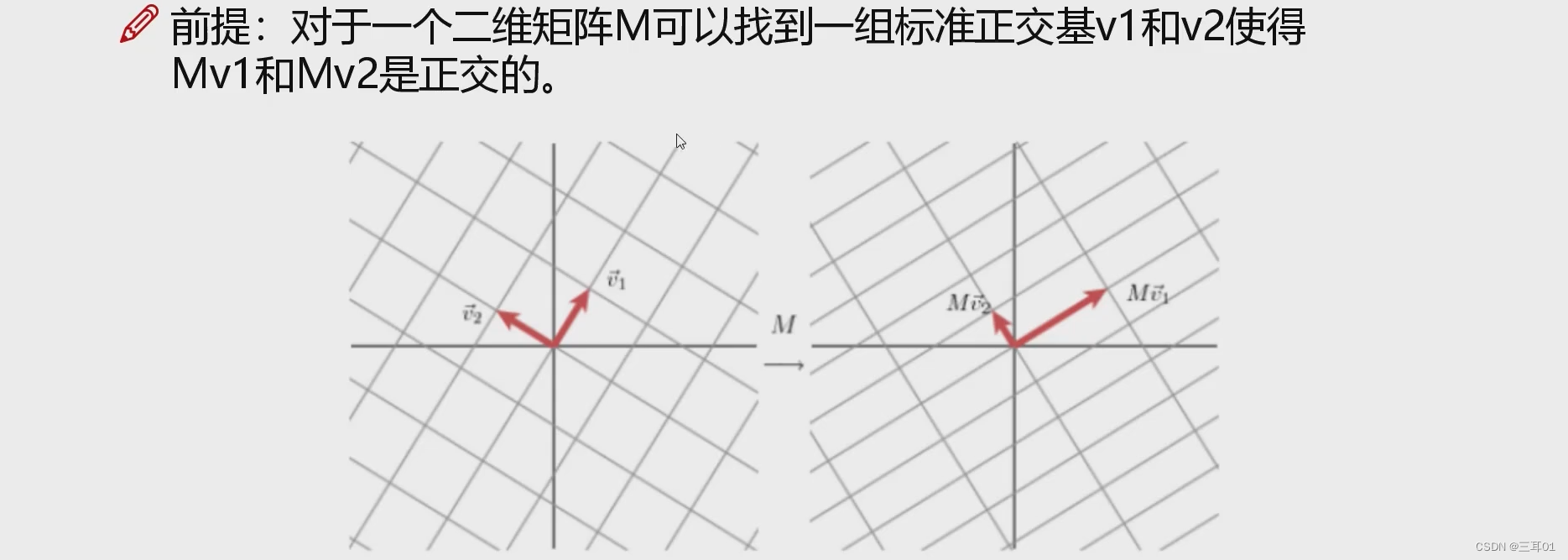
应用：
在使用线性代数的地方，基本上都要使用 SVD。 SVD 不仅仅应用在 PCA 、图像压缩、数字水印、 推荐系统和文章分类、 LSA (隐性语义分析)、特征压缩(或数据降维)中，在信号分解、信号重构、信号降噪、数据融合、同标识别、目标跟踪、故障检测和神经网络等方面也有很好的应用， 是很多机器学习算法的基石。