贪心算法
- 贪心
- 455.分发饼干
- 376.摆动序列
- 53.最大子序和
- 122.买卖股票的最佳时机||
- 55.跳跃游戏
- 45.跳跃游戏||
- 1005.K次取反后最大化的数组和
- 134.加油站
- 135.分发糖果
- 860.柠檬水找零
- 406.根据身高重建队列
- 452.用最少数量的箭引爆气球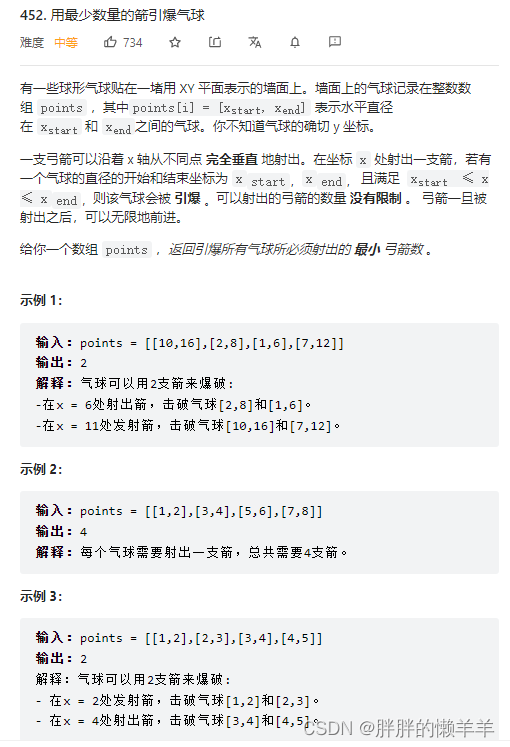
- 435.无重叠区间
- 763.划分字母区间
- 56.合并区间
- 738.单调递增的数字
贪心
455.分发饼干

思路:
要想总体上是最优解,那么局部上就要满足最优解,就要让尺寸大的饼干去让胃口大的孩子吃,而不能让尺寸很大的饼干去投喂胃口很小的孩子。,所以外层从后往前遍历孩子的胃口,内层去找满足的饼干数,这样下来就是最优解啦。
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int result=0;//喂饱的数量
int index=s.length-1;//大饼干的最后位置。
//要从孩子去遍历,找大饼干去满足
for(int i=g.length-1;i>=0;i--) {
if(index>=0&&s[index]>=g[i]) {
//较大饼干满足较大孩子的胃口了
result++;
index--;
}
}
return result;
}
376.摆动序列

思路:
1.当只有两个元素时,两个元素不一样,算两个摆动(解决:默认result=1,然后不去遍历最后一个元素)
2.第一个元素也算一个摆动。(pre=0)
3.当出现平坡的时候也算摆动。(判断条件时要加上等于0的情况)
public int wiggleMaxLength(int[] nums) {
int result=1;//初始值为1,因为要把最后的端点算进去,这样就不用遍历它了
int pre=0;//初始的坡度为0,因为要把第一个端点算上.
int post=0;//后边的坡度
for(int i=0;i<nums.length-1;i++) {
post=nums[i+1]-nums[i];
if(((pre>=0)&&(post<0))||((pre<=0)&&(post>0))) {//当满足坡度条件时
result++;
pre=post;//在if语句里边更新这个值是要防止单调平坡的情况,单调就是一直延一个方向走的情况,所以当方向改变的时候再去改变坡度的值。
}
}
return result;
}
53.最大子序和

思路:
如果前面的子序和是负数的话,那么就舍弃它从后边一位开始,因为不管后边是什么数,它都是拖后腿的。然后每次更新保存最大的值即可。
public static int maxSubArray(int[] nums) {
int start=0;
int end=0;
int result=Integer.MIN_VALUE;//更新最大的结果
int count=0;//当前的子序和
for(int i=0;i<nums.length;i++) {
count+=nums[i];
if(count>result) {
result=count;//更新最大值
end=i;
}
if(count<0) {
count=0;//当前子序和为负数,直接放弃这个,移动到下一步来更新
start=i+1;
}
}
System.out.println("start="+start);
System.out.println("end="+end);
return result;
}
122.买卖股票的最佳时机||

思路:
从第二天开始卖,收集利润为正数的利润,就是最后最大的利润。
比如1 2 3 5 7.
最后利润是6,等同于第一天买入,最后一天卖出。
public int maxProfit(int[] prices) {
int result=0;
for(int i=1;i<prices.length;i++) {
result+=Math.max(0, prices[i]-prices[i-1]);
}
return result;
}
55.跳跃游戏

思路:
每走一步,更新到当前步的最大覆盖范围,如果能覆盖到最后一个,那么就满足条件,否则,就不满足。能跳跃到的范围要保证在cover以内。
public boolean canJump(int[] nums) {
if(nums.length==1) {
return true;
}
int cover=0;
for(int i=0;i<=cover;i++) {
cover=Math.max(cover, i+nums[i]);//保证cover处于最大值
if(cover>=(nums.length-1)) {
return true;
}
}
return false;
}
45.跳跃游戏||

思路:
这道题不是去算具体的步数,而是计算最少跳几次就可以了。
要把以前遍历到的最大覆盖范围记录下来。每次都往最大的范围跳。
例如2,1,3,5,8.
第一步能跳到3的位置,但是此时还不能跳完,再去更新此时能覆盖到的最大范围。然后到了8后面的一个位置。所以说,当i走到cur的位置,如果没有遍历完,再去更新最大的覆盖范围。而最大的覆盖范围肯定是当前步数再加一步能够的到的,无论你停在前边的哪一步。都能达到这个的最大范围。
总结:当遍历到你当前的节点时,就去更新最大范围。
public int jump(int[] nums) {
if(nums.length==1) {
return 0;
}
int next=0;//代表覆盖的最大范围
int cur=0;//代表当前能移动到的步数
int result=0;
for(int i=0;i<nums.length;i++) {
next=Math.max(next,i+nums[i]);//每次更新能覆盖到的最大范围
if(cur==i) {//遍历到当前能移动的最大值了,去更新next
if(cur<nums.length) {
result++;//算移动了一步
//去更新cur的值
cur=next;
if(cur>=nums.length-1) {
break;
}
}else {
break;
}
}
}
return result;
}
1005.K次取反后最大化的数组和

思路:
这题有两个贪心策略,第一尽量将较小的负数取反,因为这样可以使结果更大。然后剩下的次数,用在绝对值最小的正数上,这样即使正数变成负数也会使代价最小。所以
先把数组按绝对值进行排序,然后把负数都变成正数。
最后看k有没有消耗完,如果没有消耗完,将绝对值最小的数改变符号即可。
public int largestSumAfterKNegations(int[] nums, int k) {
// 将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
nums = IntStream.of(nums)
.boxed()
.sorted((o1, o2) -> Math.abs(o2) - Math.abs(o1))
.mapToInt(x->x).toArray();
for(int i=0;i<nums.length;i++) {
//当遇到负数,将负数越小的值进行取反
if(k>0&&nums[i]<0) {
nums[i]=-nums[i];
k--;
}
}
//当剩下的k还是奇数的时候,将绝对值最小的正数取反即可。
if(k%2==1) {
nums[nums.length-1]=-nums[nums.length-1];
}
return IntStream.of(nums).sum();
}
134.加油站

思路:
求出每一站的净含量值,如果当前邮箱里边是负数,那么就从下一站开始。
如果邮箱总数都不能满足题意,那么直接返回-1.
为什么当前站邮箱为负数那以前的站点都不能满足呢。
可以把之前走过的站分为两个区间。
那么汽车走到这满足不了条件就代表区间1+区间2油量小于0。
如果从区间2开始走,区间2大于0的话。那么区间1肯定是小于0的,所以汽车根本不可能走到这。所以要从当前站点的下一站开始。
public int canCompleteCircuit(int[] gas, int[] cost) {
int start=0;//起始位置
int totalSum=0;//总共的邮箱净值含量
int curSum=0;//当前邮箱的含量。如果当前邮箱含量为负,那么就从下一站开始
for(int i=0;i<gas.length;i++) {
totalSum+=(gas[i]-cost[i]);
curSum+=(gas[i]-cost[i]);
if(curSum<0) {
start=i+1;
curSum=0;
}
}
if(totalSum<0) {//如果总量油都不能满足,那么从任何地方开始都不能满足题意了
return -1;
}
return start;
}
135.分发糖果

思路:
从左向右遍历一遍,保证右边分数高的孩子比左边孩子的糖果多。
从右向左遍历一遍,保证左边分数比右边分数高的孩子糖果比右边的多,同时,此时也要满足比左边孩子多的条件。
public int candy(int[] ratings) {
int []candyi=new int[ratings.length];//存糖果的数组
candyi[0]=1;//初始值为1
//从左向右遍历去分配糖果
for(int i=1;i<candyi.length;i++) {
candyi[i]=ratings[i]>ratings[i-1]?candyi[i-1]+1:1;//保证右边分数高的孩子比左边的低一个,然后默认值是1
}
//从右往左遍历去分配糖果
for(int i=candyi.length-2;i>=0;i--) {
//如果左边的孩子比右边孩子大的话
if(ratings[i]>ratings[i+1]) {
candyi[i]=Math.max(candyi[i+1]+1, candyi[i]);//保证左右两边的条件都要满足
}
}
int result=0;
for(int i:candyi) {
result+=i;
}
return result;
}
860.柠檬水找零

思路:
模拟整个过程就行,把不同的分值钞票记一个数,记录每个钞票的个数,遇到不匹配的情况返回false即可。
public boolean lemonadeChange(int[] bills) {
int five=0;
int ten=0;
int twen=0;
for(int bill:bills) {
if(bill==5) {//当收款为5的时候直接++
five++;
}
if(bill==10) {
if(five>0) {
five--;
ten++;
}else {
return false;
}
}
if(bill==20) {
if(ten>0&&five>0) {
ten--;
five--;
twen++;
}else if(five>=3) {
five-=3;
twen++;
}else {
return false;
}
}
}
return true;
}
406.根据身高重建队列

思路:
先将人按身高从大到小排列,如果身高一样,按k从小到大排列。这样就确定了一个变量,那就是前边的人一定比后边的人高,不管后边的人怎么往前插,都不会影响以及排好序的人的k。所以按身高从大到小排好序之后,只需要将人按k再进行排序即可。
public int[][] reconstructQueue(int[][] people) {
//将人根据身高从大到小排序,如果身高相同,k小的 在前边
Arrays.sort(people,(a,b)->{
if(a[0]==b[0]) {
return a[1]-b[1];
}
return b[0]-a[0];
});
LinkedList<int[]>que=new LinkedList<>();
for(int[]p:people) {
que.add(p[1],p);
}
return que.toArray(new int[people.length][]);
}
452.用最少数量的箭引爆气球
思路:
将气球左边界从小到大排序,然后判断后边的左边界是不是比上一个的右边界大,如果大,那么就需要多出来一把箭。如果不大,那么更新右边界,右边界为这两个气球中右边界较小的那个。
public int findMinArrowShots(int[][] points) {
if(points.length==0) {
return 0;
}
// 根据气球直径的开始坐标从小到大排序
// 使用Integer内置比较方法,不会溢出
Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));
int result=1;//默认就需要一个弓箭
for(int i=1;i<points.length;i++) {
if(points[i][0]>points[i-1][1]) {//当后一个气球的左边界大于前一个气球的右边界时,一定会多使用一个气球
result++;
}else {
//更新右边界为最小的那一个
points[i][1]=Math.min(points[i][1], points[i-1][1]);
}
}
return result;
}
435.无重叠区间

思路:
和扎气球那道题差不多,将所有区间先按左区间进行排序,然后如果后边的左边界小于前一个区间的右边界,那么就是边界覆盖了。然后count++.更新边界即可。
public int eraseOverlapIntervals(int[][] intervals) {
if(intervals.length==0) {
return 0;
}
//让区间根据左区间进行排序
Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
int result=0;//默认值是0
for(int i=1;i<intervals.length;i++) {
if(intervals[i][0]<intervals[i-1][1]) {//当后一个气球的左边界大于前一个气球的右边界时,一定会多使用一个气球
result++;
intervals[i][1]=Math.min(intervals[i][1], intervals[i-1][1]);//更新右边界为最小的那一个
}
}
return result;
}
763.划分字母区间

思路:
先遍历一遍数组,把每个字母出现的最右的边界记录下来。
然后第二次遍历数组的时候,right随着遍历的字母随时更新,更新的时候要保证right是最大的哪一个。
然后当i==right的时候将两个边界的差值放入结果集即可。
public List<Integer> partitionLabels(String s) {
int []hash=new int[27];//记录每个字母出现的最远距离
char []array=s.toCharArray();
for(int i=0;i<array.length;i++) {
hash[array[i]-'a']=i;
}
List<Integer> result=new ArrayList<Integer>();
int right=0;//右边界
int left=0;//左边界
for(int i=0;i<array.length;i++) {
right=Math.max(right,hash[array[i]-'a']);//保证右边界是最大的那个
if(i==right) {//当遍历到当前的最大边界时
result.add(right-left+1);
left=i+1;
}
}
return result;
}
56.合并区间

思路:
先把元素按左区间排序,如果后边的元素左边界大于上一个元素的右边界,直接加入结果集即可。如果不大于,那么更新右边界为两个边界的较大值。
public int[][] merge(int[][] intervals) {
List<int[]> res = new LinkedList<>();
//按照左边界排序
Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));
//initial start 是最小左边界
int start = intervals[0][0];
int rightmostRightBound = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
//如果左边界大于最大右边界
if (intervals[i][0] > rightmostRightBound) {
//加入区间 并且更新start
res.add(new int[]{start, rightmostRightBound});
start = intervals[i][0];
rightmostRightBound = intervals[i][1];
} else {
//更新最大右边界
rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);
}
}
res.add(new int[]{start, rightmostRightBound});
return res.toArray(new int[res.size()][]);
}
738.单调递增的数字

思路:
当发现前面的数字比后边的数字大时,前面的数字–。然后记录下当前的位置,让当前的位置以后的数字都变成9.
public int monotoneIncreasingDigits(int n) {
String s = String.valueOf(n);
char[] chars = s.toCharArray();
int start = s.length();
for (int i = s.length() - 2; i >= 0; i--) {
if (chars[i] > chars[i + 1]) {
chars[i]--;
start = i+1;
}
}
for (int i = start; i < s.length(); i++) {
chars[i] = '9';
}
return Integer.parseInt(String.valueOf(chars));
}
![[算法和数据结构]--回溯算法之DFS初识](https://img-blog.csdnimg.cn/06fa7cb876b64357b79b6fd393521712.png)
![[Pytorch]DataSet和DataLoader逐句详解](https://img-blog.csdnimg.cn/5fac6729a7374822b2c651f23afc56d9.png)