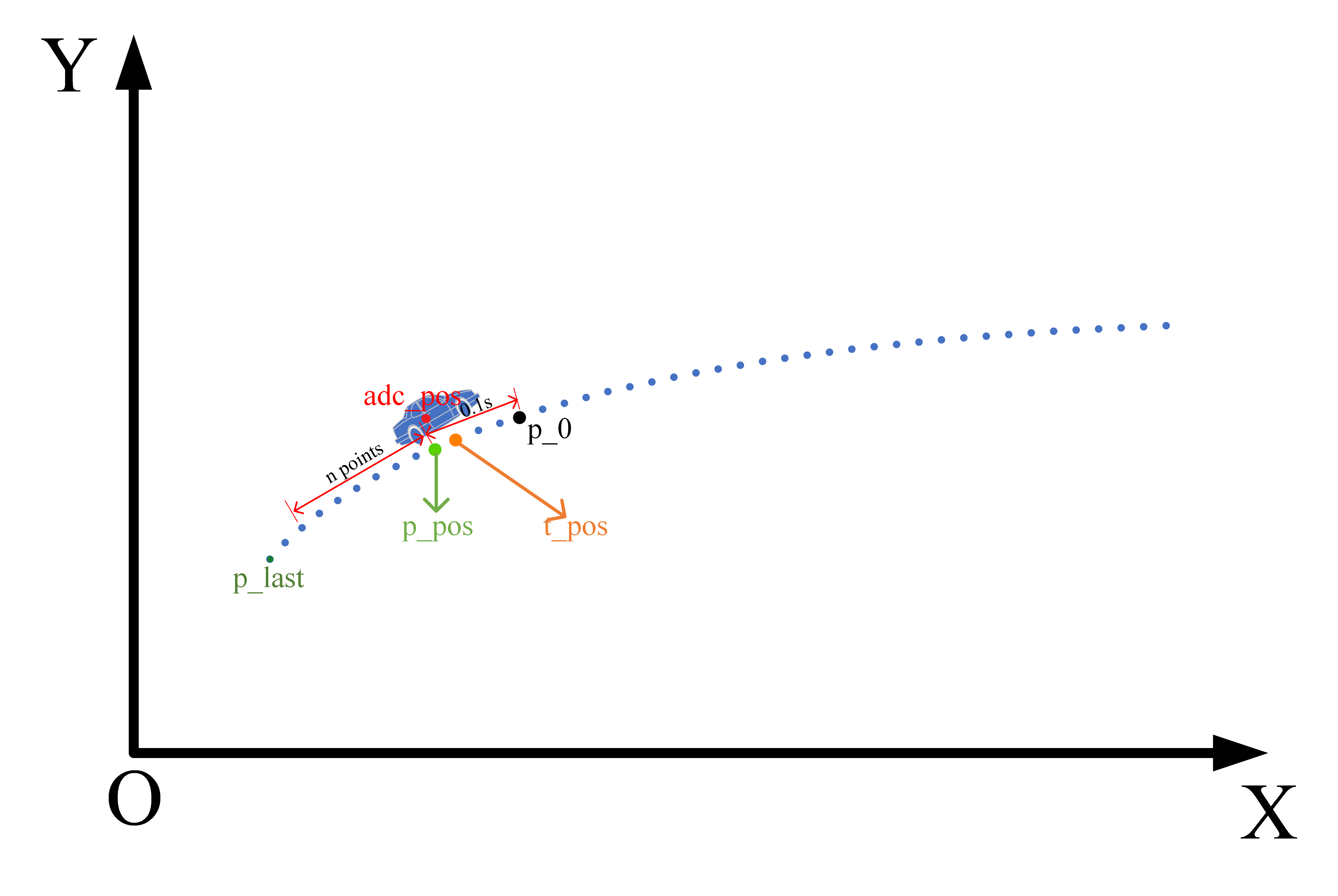
题解：

带权并查集

引言： 带权并查集是一种进阶的并查集，通常，结点i的权值等于结点i到根节点的距离，对于带权并查集，有两种操作需要掌握——Merge与Find，涉及到路径压缩与维护权值等技巧。

带权并查集的数据结构

• 使用顺序存储结构，定义结构体数组，其中a[i]的root代表节点 i 的根节点编号，weight代表它与root号节点之间的距离，也就是权值。

  struct node {
  	int root;ll weight;
  	node() :root(0), weight(0) {}
  }a[100005];
  

Find函数+权值合并

• 首先，在执行整个并查集算法之前，需要首先初始化每一个结点的根节点编号为它本身，意思就是说，每一个结点在初始状态时都被视为一颗单独的并查集树，即：

  for (int i = 1; i <= n; i++) {
      a[i].root = i;
  }
  

• 当我们想要去查询一个节点的根节点时，调用find函数：

  • 传入：想要查询的结点编号x

  • 返回： 第x号结点的根节点编号

    //路径压缩+权值合并
    int find(int x) {
     	if (x != a[x].root) {
    		//更新x的根节点
    		int tmp = a[x].root;
    		a[x].root = find(a[x].root);
    		a[x].weight += a[tmp].weight;
    	}
    	return a[x].root;
    }
    

  • 在函数体内：

    • 当结点x的root值为它自己时，即 x == a[x].root 时，直接返回a[x].root
    • 否则，递归查找它根节点的根节点
    • 在递归之前，使用tmp暂存x当前的根节点编号。这是由于在查找的过程中，我们使用了路径压缩的技巧，使a[x].root被赋值为find函数的返回值，但是在后续的计算中，我们又需要使用到这个旧的a[x].root值。
    • 在路径压缩的同时，我们必须要维护权值a[x].weight使其始终等于x号结点到a[x].root号结点的距离。
    • 在路径压缩之前，a[x].weight存储的是x到旧的root的距离，但root发生更改后，此时新的权值a[x].weight应该修改为dist(新root,旧root) + dist(旧root，x)才能符合权值的定义，dis(新root, 旧root)将会被递归计算出来，而dis(旧root, x)正是a[x].weight现在存储的值，因此，我们必须要记下旧root的编号才能找到旧root的位置，这也就是tmp发挥的作用。

合并

• 当我们得到了两个结点之间的距离，并且想要将这两个结点合并，按照并查集的思想，应当先找到他们各自的根节点，然后再将两颗树合并。然而，我们现在所获取的信息并不是根节点的信息，因此我们需要对已知的信息做一个转化：

  • 假设我们现在得到的新的信息是第l-1个节点到第r个节点的距离为w，设第l-1个节点的根节点编号为x，第r个节点的根节点编号为y。

  • 首先，我们通过$find(l-1)$和$find(r)$获得x与y的值，经过find函数内部的权值维护之后，此时，a[l-1].weight和a[r].weight已经分别被修改为l-1到x和r到y的距离了，设它们分别为w1和w2.

  • 通过上图，其实我们很容易就能看出x到y的距离为:$$w+w_2-w1$$

  • 在这，我们只需要算出x到y的距离就好了，在后续调用find函数执行路径压缩和权值合并时将会处理掉它，因此，我们合并的操作就是：

    int l, r, w;
    l = read(), r = read(), w = read();
    //x为l-1的根节点，y为r的根节点
    int x = find(l - 1), y = find(r);
    //若l-1与r的根节点不相同
    if (x != y) {
        //将结点x并入y的子树
        a[x].root = y;
        //根据向量的思想计算
        a[x].weight = w + a[r].weight - a[l - 1].weight;
    }
    

查询

写到这里，这个题目已经接近尾声。（此处再次强调a[i].weight的意义是从第i个节点到第a[i].root个节点的距离，接下来要用的） 当我们维护好了一颗带权并查集树之后，那我们查询区间和就只有两种情况：

• 设区间左端点为l，右端点为r，则
  • 当l与r的根不相同时，则无法查询出l到r的区间和。
  • 当l与r的根相同时，则有$s[l..r]=a[l-1].weight-a[r].weight$
  • 以图形的方式表达，蓝色部分即为所求的区间和：
    

完整代码：

#include <iostream>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;
ll n, m, q;

//带权并查集结点
struct node {
    int root;ll weight;
    node() :root(0), weight(0) {}
}a[100005];
//快读
int read() {
    char ch = getchar(); int res = 0;
    while (ch < '0' || ch>'9') {
        ch = getchar();
    }
    while (!(ch < '0' || ch>'9')) {
        res = res * 10 + (ch - '0');
        ch = getchar();
    }
    return res;
}
//快写
void print(ll x) {
    if (x > 9) {
        print(x / 10);
    }
    putchar(x % 10 + '0');
}

//路径压缩+权值合并
int find(int x) {
    if (x != a[x].root) {
        //更新x的根节点
        int tmp = a[x].root;
        a[x].root = find(a[x].root);
        a[x].weight += a[tmp].weight;
    }
    return a[x].root;
}

int main()
{
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++) {
        a[i].root = i;
    }
    for (int i = 1; i <= m; i++) {
        int l, r, w;
        l = read(), r = read(), w = read();
        //x为l-1的根节点，y为r的根节点
        int x = find(l - 1), y = find(r);
        //若l-1与r的根节点不相同
        if (x != y) {
            //将结点x并入y的子树
            a[x].root = y;
            //根据向量的思想计算
            a[x].weight = w + a[r].weight - a[l - 1].weight;
        }
    }
    for (int i = 1; i <= q; i++) {
        int l, r; cin >> l >> r;
        if (find(l - 1) != find(r)) {
            puts("UNKNOWN");
        }
        else {
            print(a[l - 1].weight - a[r].weight);
            putchar('\n');
        }
    }
    return 0;
}