---

本文只做简介，关于贝塞尔曲线和B样条曲线的详细介绍，请参考：详解样条曲线（上）（包含贝塞尔曲线）
部分图片来源于：https://zhuanlan.zhihu.com/p/344934774

一、贝塞尔曲线

讲之前，我们先看一张图：

这里的 P0、P1、P2 分别称之为控制点，贝塞尔曲线的产生完全与这三个点位置相关。

这也就意味着，我们可以通过调节控制点的位置，进而调整整个曲线。

那么，似乎最开始的控制点，也不一定是三个？如果是四个、五个，甚至更多呢？

如此一来，你会发现贝塞尔曲线内的递归结构。实际上，上述介绍的分别是三阶、四阶、五阶的贝塞尔曲线，贝塞尔曲线可以由阶数递归定义。

一个在线玩贝塞尔曲线的链接：在线玩贝塞尔曲线

下面直接给贝塞尔曲线的通用公式

假设一共有 $\mathrm{n}+1$ 个点 ${\mathrm{P}}_0,{\mathrm{P}}_1,\cdots ,{\mathrm{P}}_{\mathrm{n}}$ ，这 $\mathrm{n}+1$ 个点确定了 $\mathrm{n}$ 次的贝塞尔曲线。
$n$ 阶贝塞尔曲线 $B^n(t)$ 可以由前 $n$ 个点决定的 $n-1$ 次贝塞尔曲线 $B^{n-1}\left(t\mid P_0,\cdots ,P_{n-1}\right)$ 与后 $n$ 个点决定的 $n-1$ 次贝塞尔曲线 ${\mathrm{B}}^{\mathrm{n}-1}\left(\mathrm{t}\mid {\mathrm{P}}_1,\cdots ,{\mathrm{P}}_{\mathrm{n}}\right)$ 线性组合递推而来，即
$${\mathrm{B}}^{\mathrm{n}}\left(\mathrm{t}\mid {\mathrm{P}}_0,{\mathrm{P}}_1,\cdots ,{\mathrm{P}}_{\mathrm{n}}\right)=(1-\mathrm{t}){\mathrm{B}}^{\mathrm{n}-1}\left(\mathrm{t}\mid {\mathrm{P}}_0,{\mathrm{P}}_1,\cdots ,{\mathrm{P}}_{\mathrm{n}-1}\right)+\mathrm{t}{\mathrm{B}}^{\mathrm{n}-1}\left(\mathrm{t}\mid {\mathrm{P}}_1,{\mathrm{P}}_2,\cdots ,{\mathrm{P}}_{\mathrm{n}}\right)$$
且一次贝塞尔曲线，即为由两点决定的线段，也即
$${\mathrm{B}}^1\left(\mathrm{t}\mid {\mathrm{P}}_0,{\mathrm{P}}_1\right)=(1-\mathrm{t}){\mathrm{P}}_0+{\mathrm{tP}}_1$$
可以得到 $\mathrm{n}$ 次贝塞尔曲线的表达通式为
$$B(t)=\sum _{i=0}^n{C}_n^i(1-t{)}^{n-i}{t}^i{P}_i$$

有了通用公式，我们就可以通过遍历t来离散化贝塞尔曲线了！

二、B样条曲线

几个概念

• 控制点: 也就是控制曲线的点，等价于贝塞尔函数的控制点，通过控制点可以控制曲线形状。假设有 $n+1$ 个控制点 ${\mathrm{P}}_0,{\mathrm{P}}_1,{\mathrm{P}}_2,\cdots ,{\mathrm{P}}_{\mathrm{n}}$
• 节点: 这个跟控制点没有关系，而是人为地将目标曲线分为若干个部分，其目的就是尽量使得各个部分有所影响但也有一定独立性， 这也是为什么B样条中，有时一个控制点的改变，不会很大影响到整条曲线，而只影响到局部的原因，这是区别于贝塞尔曲线的一 点。节点划分影响到权重计算，可以预想到的是，实现局部性的影响的原理应该是在生成某区间内的点时，某些控制点前的权重值会 为 0 ，即对该点没有贡献，所以才有上述特点。事实上，就是如此的。先了解有这个概念即可。假设我们划分了 $m+1$ 个节点 ${\mathrm{t}}_0,{\mathrm{t}}_1,\cdots ,{\mathrm{t}}_{\mathrm{m}}$ ，将曲线分成了 $\mathrm{m}$ 段
• 次与阶：次的概念就是贝塞尔中次的概念，即权重中 $t$ 的最高幂次。而 阶=次 +1 。这里只需要知道次这个概念即可。假设我们用 $k$ 表示次，即 $\mathrm{k}$ 次。

B 样条曲线比贝塞尔曲线的设计要复杂许多，我们直接通过他们的公式大致比较一下贝塞尔曲线与 B 样条曲线的区别：

贝塞尔曲线

$$B(t)=\sum _{i=0}^n{C}_n^i(1-t{)}^{n-i}{t}^i{P}_i,t\in [0,1]$$

B样条曲线

对于 $n+1$ 个控制点 $P_0,P_1,\cdots ,P_n$ ，有一个包含 $m+1$ 个节点的列表 (或节点向量) $t_0,t_1,\cdots ,t_m$ ，其 $k$ 次 $B$ 样条曲线表达式为 (且 $m=n+k+1)$

$$\mathrm{P}(\mathrm{t})=\sum _{\mathrm{i}=0}^{\mathrm{n}}{\mathrm{B}}_{\mathrm{i},\mathrm{k}}(\mathrm{t}){\mathrm{P}}_{\mathrm{i}}$$

可以发现，B样条曲线的核心就是 ${\mathrm{B}}_{\mathrm{i},\mathrm{k}}(\mathrm{t})$ ，它被称为 k 次 B 样条基函数，也叫调和函数。

它满足如下递推式（deBoor递推式）：

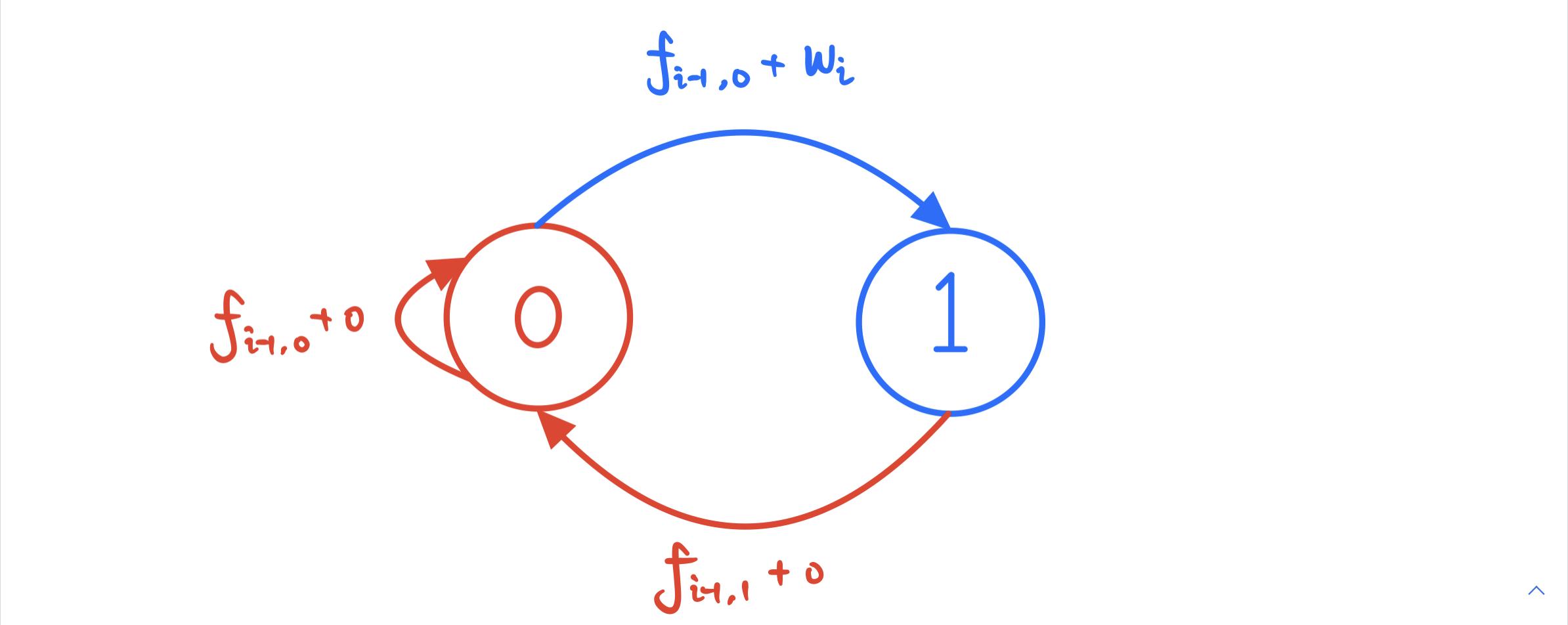
$$\begin{array}{c}\mathrm{k}=0,{\mathrm{B}}_{\mathrm{i},0}(\mathrm{t})=\{\begin{array}{ll}1,& \mathrm{t}\in \left[{\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}}+1\right]\\ 0,& \text{ Otherwise }\end{array}\\ \mathrm{k}>0,{\mathrm{B}}_{\mathrm{i},\mathrm{k}}(\mathrm{t})=\frac{\mathrm{t}-{\mathrm{t}}_{\mathrm{i}}}{{\mathrm{t}}_{\mathrm{i}+\mathrm{k}}-{\mathrm{t}}_{\mathrm{i}}}{\mathrm{B}}_{\mathrm{i},\mathrm{k}-1}(\mathrm{t})+\frac{{\mathrm{t}}_{\mathrm{i}+\mathrm{k}+1}-\mathrm{t}}{{\mathrm{t}}_{\mathrm{i}+\mathrm{k}+1}-{\mathrm{t}}_{\mathrm{i}+1}}{\mathrm{B}}_{\mathrm{i}+1,\mathrm{k}-1}(\mathrm{t})\end{array}$$

三、Python 代码实现B样条曲线离散化

import time

import numpy as np
from matplotlib import pyplot as plt


def getB(i, k, t, T, B):
    '''
    获取B[i][k]的值
    :param i: B样条基函数矩阵行索引
    :param k: 当前阶数（B样条基函数矩阵列索引）
    :param t: 当前t值
    :param T: 节点值列表
    :param B: B样条基函数矩阵
    :return: B[i][k]的值
    '''
    if B[i, k] < 0:
        if k == 0:
            if T[i] <= t <= T[i + 1]:
                B[i, k] = 1
            else:
                B[i, k] = 0
        else:
            w1 = w2 = 0
            if T[i + k] - T[i] != 0:
                w1 = (t - T[i]) / (T[i + k] - T[i])
            if T[i + k + 1] - T[i + 1] != 0:
                w2 = (T[i + k + 1] - t) / (T[i + k + 1] - T[i + 1])
            B[i, k] = w1 * getB(i, k - 1, t, T, B) + w2 * getB(i + 1, k - 1, t, T, B)
    return B[i][k]


def plot_spline(P, K, T):
    '''
    根据P、K、T绘制离散化的B样条曲线及其控制点
    :param P: 控制点列表
    :param K: B样条曲线阶数
    :param T: 节点值列表
    :return: None
    '''
    startTime = time.time()
    t = min(T)
    step = T[-1] / 100
    X, Y = [], []
    while t <= max(T):
        B = np.zeros((len(T) - 1, K + 1))
        B.fill(-1)
        x = y = 0
        for i in range(len(P)):
            b = getB(i, K, t, T, B)
            x += b * P[i][0]
            y += b * P[i][1]
        X.append(x)
        Y.append(y)
        t += step
    print("用时:", (time.time() - startTime), "s")
    plt.plot(X, Y, marker='o', label="fit point")
    plt.scatter([p[0] for p in P], [p[1] for p in P], color="red", label="control point")
    plt.legend()
    plt.show()


if __name__ == '__main__':
    '''
    P: 控制点列表
    T: 节点值列表
    K: B样条曲线阶数
    '''

    # 测试案例1
    P = [[50, 50], [100, 300], [300, 100], [380, 200], [400, 600]]
    T = [0, 0, 0, 4 / 9, 5 / 9, 1, 1, 1]
    K = 2
    plot_spline(P, K, T)

    # 测试案例2
    P = [[2982.51, 9384.89], [3478.42, 4212.45], [9353.02, 6690.64], [4635.54, 1810.51], [12951.5, 5940.83],
         [7458.4, 10299.9], [14973.3, 7948.8], [8780.82, 11392.9], [14792.3, 10948.1]]
    T = [0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 6, 6, 6]
    K = 3
    plot_spline(P, K, T)

控制台输出

用时: 0.001992940902709961 s
用时: 0.003986835479736328 s

结果展示

四、C++ 代码实现B样条曲线离散化

4.1 主要代码

// 递归填B表
double getBValue(int i, int k, double t, vector<double> kVector, vector<vector<double>> B){
	if (B[i][k] == NULL){
		if (k == 0){
			if (kVector[i] <= t && kVector[i + 1] >= t){
				B[i][k] = 1;
			}
			else{
				B[i][k] = 0;
			}
		}
		else{
			double w1 = 0;
			double w2 = 0;
			if (kVector[i + k] - kVector[i] != 0){
				w1 = (t - kVector[i]) / (kVector[i + k] - kVector[i]);
			}
			if (kVector[i + k + 1] - kVector[i + 1] != 0){
				w2 = (kVector[i + k + 1] - t) / (kVector[i + k + 1] - kVector[i + 1]);
			}
			B[i][k] = w1 * getBValue(i, k - 1, t, kVector, B) + w2 * getBValue(i + 1, k - 1, t, kVector, B);
		}
	}
	return B[i][k];
}

// B样条曲线离散化
DXFPolyLineEntities splineDiscretization(DXFSpline spline){
	DXFPolyLineEntities poly = DXFPolyLineEntities();
	int K = spline.degree;
	// 获取kVector
	vector<double> kVector(spline.kVector.size());
	for (int i = 0; i < spline.kVector.size(); i++){
		kVector[i] = spline.kVector[i].k;
	}
	// 根据函数获得离散点
	for (double t = kVector[0]; t <= kVector[spline.nKnots - 1]; t += (kVector[spline.nKnots - 1] / SPLINE_D)){
		double x = 0.0;
		double y = 0.0;
		// 初始化B表
		vector<vector<double>> B(spline.nKnots - 1, vector<double>(K + 1,NULL));
		// 遍历控制点集合
		for (int i = 0; i < spline.controlPointVector.size(); i++){
			// 已知 i,K,t, 推出B值
			double bValue = getBValue(i, K, t, kVector, B);
			x += (bValue * spline.controlPointVector[i].x);
			y += (bValue * spline.controlPointVector[i].y);
		}
		poly.vertex.push_back(DL_VertexData(x, y));
	}
	return poly;
}

4.2 其余类

//多段线实体对象
class DXFPolyLineEntities
{
public:
	vector<DL_VertexData> vertex;//顶点
	bool isclose;//闭合标志位
};

/**
 * Vertex Data.
 */
struct DXFLIB_EXPORT DL_VertexData {
    /**
     * Constructor.
     * Parameters: see member variables.
     */
    DL_VertexData(double px=0.0, double py=0.0, double pz=0.0,
                  double pBulge=0.0) {
        x = px;
        y = py;
        z = pz;
        bulge = pBulge;
    }

    /*! X Coordinate of the vertex. */
    double x;
    /*! Y Coordinate of the vertex. */
    double y;
    /*! Z Coordinate of the vertex. */
    double z;
    /*! Bulge of vertex.
     * (The tangent of 1/4 of the arc angle or 0 for lines) */
    double bulge;
};

// 样条曲线对象
class DXFSpline
{
public:
	// 样条曲线的阶数
	int degree;
	// 节点数
	int nKnots;
	// 控制点数
	int nControl;
	// 拟合点数（如果有）
	int nFit;
	// 样条曲线标志（按位编码）
	// 1 = 闭合样条曲线;
	// 2 = 周期样条曲线;
	// 4 = 有理样条曲线;
	// 8 = 平面;
	// 16 = 线性（同时设置平面位）
	int flags;

	// 相切开始和结束点坐标
	double tangentStartX;
	double tangentStartY;
	double tangentStartZ;
	double tangentEndX;
	double tangentEndY;
	double tangentEndZ;

	// 控制点集合
	vector<DL_ControlPointData> controlPointVector;
	// 拟合点集合
	vector<DL_FitPointData> fitPointVector;
	// 节点值集合
	vector<DL_KnotData> kVector;
};

/**
* Spline control point data.
*/
struct DXFLIB_EXPORT DL_ControlPointData {
	/**
	* Constructor.
	* Parameters: see member variables.
	*/
	DL_ControlPointData(){}
	DL_ControlPointData(double px, double py, double pz, double weight) {
		x = px;
		y = py;
		z = pz;
		w = weight;
	}

	/*! X coordinate of the control point. */
	double x;
	/*! Y coordinate of the control point. */
	double y;
	/*! Z coordinate of the control point. */
	double z;
	/*! Weight of control point. */
	double w;
};

/**
* Spline fit point data.
*/
struct DXFLIB_EXPORT DL_FitPointData {
	/**
	* Constructor.
	* Parameters: see member variables.
	*/
	DL_FitPointData(){}
	DL_FitPointData(double x, double y, double z) : x(x), y(y), z(z) {}

	/*! X coordinate of the fit point. */
	double x;
	/*! Y coordinate of the fit point. */
	double y;
	/*! Z coordinate of the fit point. */
	double z;
};

/**
* Spline knot data.
*/
struct DXFLIB_EXPORT DL_KnotData {
	/**
	* Constructor.
	* Parameters: see member variables.
	*/
	DL_KnotData() {}
	DL_KnotData(double pk) {
		k = pk;
	}

	/*! Knot value. */
	double k;
};

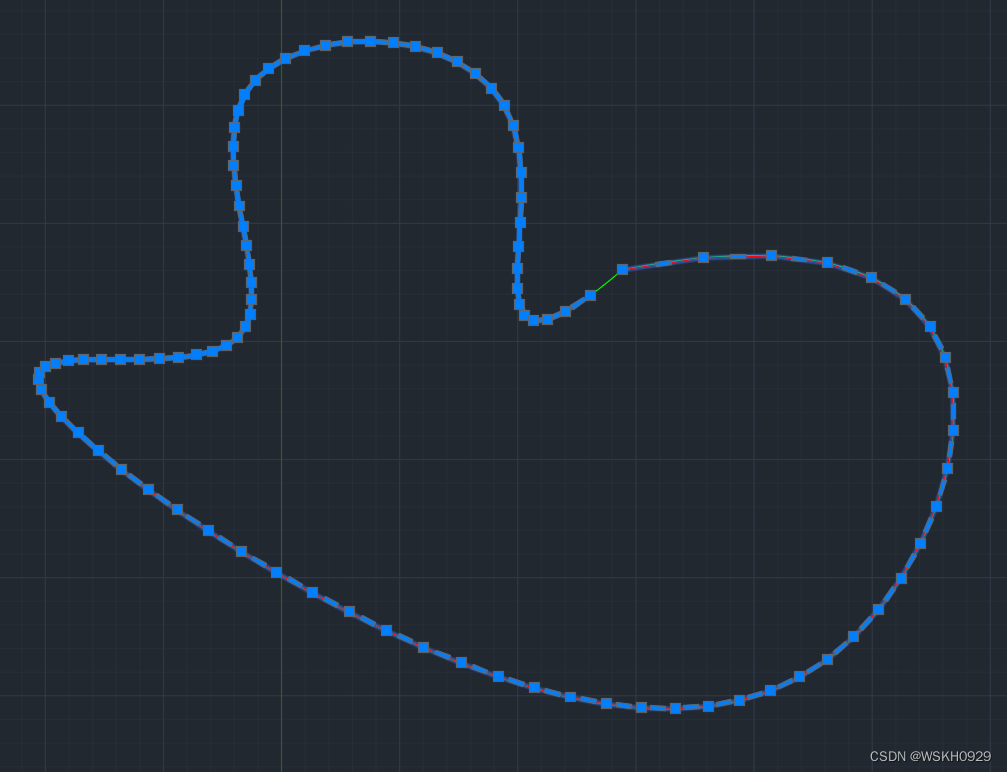
4.3 离散效果展示（在CAD中展示）

案例1

案例2

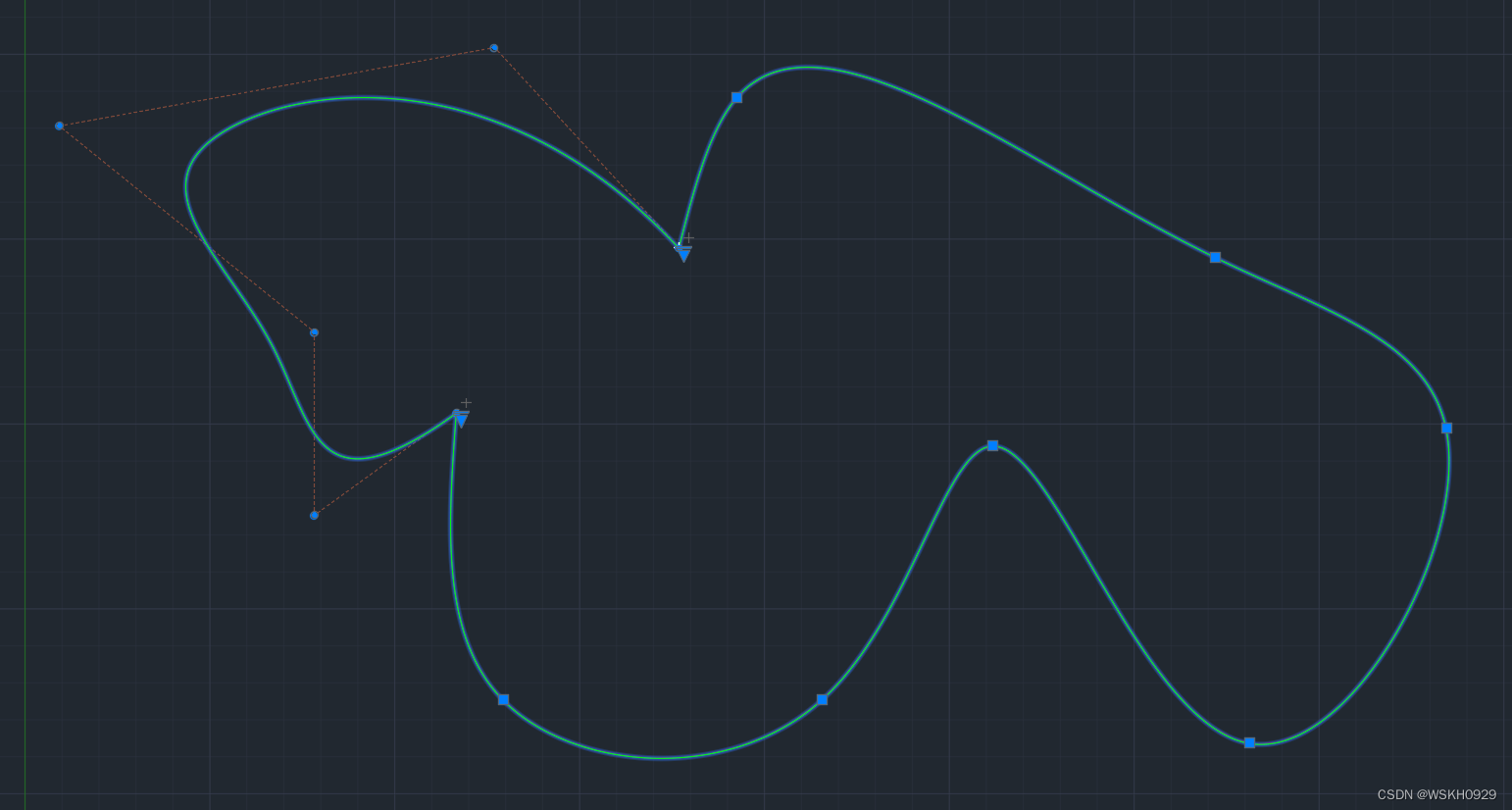
案例3