使用Python通过拉马努金公式快速求π
一、前言
π是一个数学常数,定义为:圆的周长与直径的比值。
π是一个无理数,也是一个超越数,它的小数部分无限不循环。
π可以用来精确计算圆周长、圆面积、球体积等几何形状的关键值。
有关π的有趣知识有很多,例如:
- π在数学中有很多重要的应用,例如欧拉公式e^(iπ)=-1,这个公式被称为“数学之美”,因为它将5个看似无关的符号紧密地联系了起来。
- π符号是由瑞士数学家欧拉在1736年首次使用的。之前,人们通常用分数或无穷级数来表示圆周率。
- π是希腊语“周长”的开头字母。
- π的小数部分中,第762位到第766位是“99999”,这被称为“Feynman点”,因为物理学家费曼(Richard Feynman)曾经说过,如果他能记住π的所有数字,他就会以这五个9为结尾。
- 3月14日被称为“圆周率日”,因为这个日期的美式写法是3/14,和π的前两位数字相同。
- 7月22日也被称为“圆周率近似日”,因为这个日期的欧式写法是22/7,和π的一个常用近似值相同。
π是否是一个正规数还没有确定,正规数是指在任何进制下,它的小数部分包含了所有可能出现的数字序列。但是目前还没有确定的答案。
一种可能的情况是,π是一个正规数,也就是说它在任何进制下的小数部分包含了所有可能出现的数字序列,并且每个数字出现的概率都相同。如果这样的话,由于π是一个无限不循环小数,那么π中所有数字出现的概率确实均等。也就是说,我们在π中找到任何数字的组合,比如: - 所有人的生日
- 所有人的银行卡密码
这里介绍一个在π中查找特殊数字组合起始位置的网站:
http://www.subidiom.com/pi/pi.asp
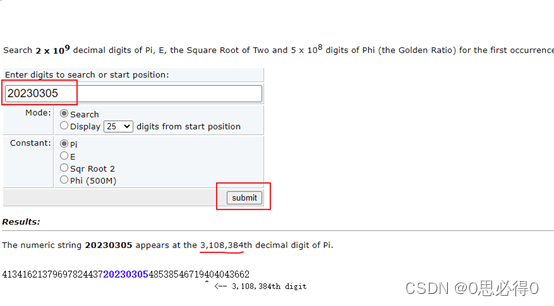
只要输入一个你想在π中找寻的数字组合,这个网站就会通过在π中搜索并反馈搜索结果给你:
- 进入网站,输入想要查询的数字组合:20230305
- 点击
submit - 等待查询结果:3108384
1.1 为什么要算π
π是一个无理数,也就是说它不能用两个整数的比值来表示。它的小数部分是无限不循环的,目前已经计算出了超过50万亿位。
实际上,如果用圆周公式来计算整个宇宙的周长,只需要使用π的前40位就可以精确计算出来了,我们假设宇宙的直径是93亿光年,那么它的周长就是2π×93亿光年。如果我们用π的前40位来计算这个值,那么误差就不到一个质子的直径。也就是说,用π的前40位就足以精确地描述宇宙的大小了。
那为什么还要用超级计算机不停的计算π呢?用超级计算机不停的算π,是因为人们对这个神奇的数有着强烈的好奇心和探索欲。
一方面,计算π可以检验超级计算机的性能和稳定性,也可以推动计算方法和软件技术的发展。
另一方面,计算π也有一些实际应用,比如密码学、随机数生成、数据压缩等。
不过,由于π是一个无理数,它的小数部分是无限不循环的,所以用任何有限的资源都无法算尽它。
1.2 π的求法
π在历史上被不同的文明用不同的方法估算过,最早可以追溯到4000年前的古埃及和巴比伦。其中一个简单的方法是用绳子测量圆形物体的周长和直径,然后计算它们的比值。
求π值的方法有很多种,比如:
阿基米德法:用正多边形逼近圆,计算其周长和面积,得到π的上下界。
无穷级数法:利用一些收敛速度快的无穷级数公式,如莱布尼茨公式、马青公式等,不断求和得到π的近似值。
莱布尼茨公式:π/4 = 1 - 1/3 + 1/5 - 1/7 + …
马青公式:π = 16 arctan(1/5) - 4 arctan(1/239)
阿基米德法变形:π = 2 + 2/3 + 2/3x2/5 + 2/3x2/5x3/7 + …
蒙特卡罗法:用随机数模拟撒豆子或者投针实验,统计落在圆内和圆外的比例,得到π的近似值。
今天要介绍的是是拉马努金公式(Ramanujan formula),它是印度数学家拉马努金(Srinivasa Ramanujan)在1910年发现的一系列级数公式,可以用来快速计算π的近似值。这个公式每计算一项可以得到8位的十进制精度。
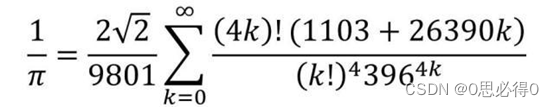
二、准备
2.1 高精度库
在Python中,默认的小数位数为17位,如果想要计算更多的小数位,则需要专门的库。这里使用decimal库。decimal是一个Python内置库,无需安装。可以直接导入使用。
2.2 π的值
因为后面要涉及到核对,所以需要准备正确的π的前xx位,这里是使用了前1万位。如下:
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315155748572424541506959508295331168617278558890750983817546374649393192550604009277016711390098488240128583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912933136770289891521047521620569660240580381501935112533824300355876402474964732639141992726042699227967823547816360093417216412199245863150302861829745557067498385054945885869269956909272107975093029553211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000816470600161452491921732172147723501414419735685481613611573525521334757418494684385233239073941433345477624168625189835694855620992192221842725502542568876717904946016534668049886272327917860857843838279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863067442786220391949450471237137869609563643719172874677646575739624138908658326459958133904780275900994657640789512694683983525957098258226205224894077267194782684826014769909026401363944374553050682034962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382686838689427741559918559252459539594310499725246808459872736446958486538367362226260991246080512438843904512441365497627807977156914359977001296160894416948685558484063534220722258284886481584560285060168427394522674676788952521385225499546667278239864565961163548862305774564980355936345681743241125150760694794510965960940252288797108931456691368672287489405601015033086179286809208747609178249385890097149096759852613655497818931297848216829989487226588048575640142704775551323796414515237462343645428584447952658678210511413547357395231134271661021359695362314429524849371871101457654035902799344037420073105785390621983874478084784896833214457138687519435064302184531910484810053706146806749192781911979399520614196634287544406437451237181921799983910159195618146751426912397489409071864942319615679452080951465502252316038819301420937621378559566389377870830390697920773467221825625996615014215030680384477345492026054146659252014974428507325186660021324340881907104863317346496514539057962685610055081066587969981635747363840525714591028970641401109712062804390397595156771577004203378699360072305587631763594218731251471205329281918261861258673215791984148488291644706095752706957220917567116722910981690915280173506712748583222871835209353965725121083579151369882091444210067510334671103141267111369908658516398315019701651511685171437657618351556508849099898599823873455283316355076479185358932261854896321329330898570642046752590709154814165498594616371802709819943099244889575712828905923233260972997120844335732654893823911932597463667305836041428138830320382490375898524374417029132765618093773444030707469211201913020330380197621101100449293215160842444859637669838952286847831235526582131449576857262433441893039686426243410773226978028073189154411010446823252716201052652272111660396665573092547110557853763466820653109896526918620564769312570586356620185581007293606598764861179104533488503461136576867532494416680396265797877185560845529654126654085306143444318586769751456614068007002378776591344017127494704205622305389945613140711270004078547332699390814546646458807972708266830634328587856983052358089330657574067954571637752542021149557615814002501262285941302164715509792592309907965473761255176567513575178296664547791745011299614890304639947132962107340437518957359614589019389713111790429782856475032031986915140287080859904801094121472213179476477726224142548545403321571853061422881375850430633217518297986622371721591607716692547487389866549494501146540628433663937900397692656721463853067360965712091807638327166416274888800786925602902284721040317211860820419000422966171196377921337575114959501566049631862947265473642523081770367515906735023507283540567040386743513622224771589150495309844489333096340878076932599397805419341447377441842631298608099888687413260472156951623965864573021631598193195167353812974167729478672422924654366800980676928238280689964004824354037014163149658979409243237896907069779422362508221688957383798623001593776471651228935786015881617557829735233446042815126272037343146531977774160319906655418763979293344195215413418994854447345673831624993419131814809277771038638773431772075456545322077709212019051660962804909263601975988281613323166636528619326686336062735676303544776280350450777235547105859548702790814356240145171806246436267945612753181340783303362542327839449753824372058353114771199260638133467768796959703098339130771098704085913374641442822772634659470474587847787201927715280731767907707157213444730605700733492436931138350493163128404251219256517980694113528013147013047816437885185290928545201165839341965621349143415956258658655705526904965209858033850722426482939728584783163057777560688876446248246857926039535277348030480290058760758251047470916439613626760449256274204208320856611906254543372131535958450687724602901618766795240616342522577195429162991930645537799140373404328752628889639958794757291746426357455254079091451357111369410911939325191076020825202618798531887705842972591677813149699009019211697173727847684726860849003377024242916513005005168323364350389517029893922334517220138128069650117844087451960121228599371623130171144484640903890644954440061986907548516026327505298349187407866808818338510228334508504860825039302133219715518430635455007668282949304137765527939751754613953984683393638304746119966538581538420568533862186725233402830871123282789212507712629463229563989898935821167456270102183564622013496715188190973038119800497340723961036854066431939509790190699639552453005450580685501956730229219139339185680344903982059551002263535361920419947455385938102343955449597783779023742161727111723643435439478221818528624085140066604433258885698670543154706965747458550332323342107301545940516553790686627333799585115625784322988273723198987571415957811196358330059408730681216028764962867446047746491599505497374256269010490377819868359381465741268049256487985561453723478673303904688383436346553794986419270563872931748723320837601123029911367938627089438799362016295154133714248928307220126901475466847653576164773794675200490757155527819653621323926406160136358155907422020203187277605277219005561484255518792530343513984425322341576233610642506390497500865627109535919465897514131034822769306247435363256916078154781811528436679570611086153315044521274739245449454236828860613408414863776700961207151249140430272538607648236341433462351897576645216413767969031495019108575984423919862916421939949072362346468441173940326591840443780513338945257423995082965912285085558215725031071257012668302402929525220118726767562204154205161841634847565169998116141010029960783869092916030288400269104140792886215078424516709087000699282120660418371806535567252532567532861291042487761825829765157959847035622262934860034158722980534989650226291748788202734209222245339856264766914905562842503912757710284027998066365825488926488025456610172967026640765590429099456815065265305371829412703369313785178609040708667114965583434347693385781711386455873678123014587687126603489139095620099393610310291616152881384379099042317473363948045759314931405297634757481193567091101377517210080315590248530906692037671922033229094334676851422144773793937517034436619910403375111735471918550464490263655128162288244625759163330391072253837421821408835086573917715096828874782656995995744906617583441375223970968340800535598491754173818839994469748676265516582765848358845314277568790029095170283529716344562129640435231176006651012412006597558512761785838292041974844236080071930457618932349229279650198751872127267507981255470958904556357921221033346697499235630254947802490114195212382815309114079073860251522742995818072471625916685451333123948049470791191532673430282441860414263639548000448002670496248201792896476697583183271314251702969234889627668440323260927524960357996469256504936818360900323809293459588970695365349406034021665443755890045632882250545255640564482465151875471196218443965825337543885690941130315095261793780029741207665147939425902989695946995565761218656196733786236256125216320862869222103274889218654364802296780705765615144632046927906821207388377814233562823608963208068222468012248261177185896381409183903673672220888321513755600372798394004152970028783076670944474560134556417254370906979396122571429894671543578468788614445812314593571984922528471605049221242470141214780573455105008019086996033027634787081081754501193071412233908663938339529425786905076431006383519834389341596131854347546495569781038293097164651438407007073604112373599843452251610507027056235266012764848308407611830130527932054274628654036036745328651057065874882256981579367897669742205750596834408697350201410206723585020072452256326513410559240190274216248439140359989535394590944070469120914093870012645600162374288021092764579310657922955249887275846101264836999892256959688159205600101655256375678
三、代码
from decimal import Decimal, getcontext # 高精度小数库
from mdTools import ftDecTimeIt # 计算函数运行时长的装饰器
from math import factorial # 阶乘
from π import str_real_pi # π的真实值(前1万位小数)
count_numbers = 5000 # 要计算的前N位,请勿超过10000,否则无数据核对
effective_numbers = int(count_numbers * 1.1) # 有效数字位数
print(f'本程序即将计算π的前:{count_numbers}位,并核对。')
@ftDecTimeIt(1)
def count_π(prec=1000):
getcontext().prec = prec # 设置有效的数字位数
x = 0
for k in range(int(prec / 8) + 1): # 这个公式每计算一项可以得到8位的十进制精度。
a = 2 * Decimal.sqrt(Decimal(2)) / 9801
b = factorial(4 * k) * (1103 + 26390 * k)
c = pow(factorial(k), 4) * pow(396, 4 * k)
x = x + a * b / c
return 1 / x
pi = count_π(effective_numbers)
# 核对
flag = True
for i in range(2, count_numbers):
if str_real_pi[i] != str(pi)[i]:
print(f'出错啦!出错的位数为:{i}, 该小数位正确的为:{str_real_pi[i]}, 错误的计算为:{str(pi)[i]}')
flag = False
break
if flag:
print('核对无误!')
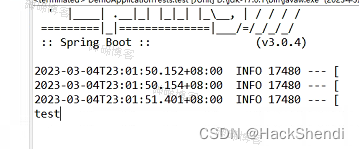
本程序即将计算π的前:5000位,并核对。
函数 count_π 运行 1 次的总耗时为:18.5894 秒
核对无误!
> 本程序即将计算π的前:5000位,并核对。
> 函数 count_π 运行 1 次的总耗时为:18.5894 秒
> 核对无误!