md,离开学校好多年了,这些基础趁现在还记得记录一下,不然怕哪天还给老师就尴尬了,方便复习
基本概念
- 二进制:(逢2进1)由0和1组成。
- 十六进制:(逢16进1)由0-9,A-F组成。
- 各种进制数的后缀字母分别为:
- B :二进制数 (binary)。
- O :八进制数 (octal)。
- D :十进制数 (decimal)。
- H :十六进制数 (hexadecimal)(十六进制一般会以“0x”开头,或以“H”结尾。
- 十进制数通常不加后缀,十进制数后的字母 D 可省略。
二进制转化为十进制
1、无符号整数二进制数转化为十进制
无符号整数的二进制转化为十进制数,从二进制数的右边第一位起,从右往左,先用二制位置上的数乘以2的相应位数的幂,然后把每一位的乘积相加即可得到二进制数对应的十进制数。
【例题】把二进制数1101001转化为十进制数。
解析:从二进制数1101001右边第一位开始,第一位的数字是1,则有1 * 2^0 =1,第二位的数字是0,则有0 * 2^1 =0,第三位的数字是0,则有0 * 2^2 =0,第四位数字是1,则有1 * 2^3 =8,第五位数字是0,则有0 * 2^4 =0,第六位数字是1,则有1 * 2^5 =32,第七位数字是1,则有1 * 2^6 =64。
再把所有积相加即可得1+0+0+8+0+32+64=105,故二进制数1101001转化为十进制数是105。
2、带符号二进制整数转化为十进制数
带符号的二进制数转化为十进制数,先观察二进制数最高位是什么数,如果是1,则表示是负数,如果是0则表示是正数,确定符号后再来转化为十进制数。
【例题】把带符号的二进制数10000000 00010000转化为十进制数。
解析:带符号的二进制数原码,最高位代表的是符合位,我们先观察最高位是1,则表示这个是负数,故可求得此二进制数对应的十进制数是
-(0 * 2^0 + … + 1 * 2^4 + … )=-16。
3、小数转化为十进制数
小数的二进制数转化为十进制数的方法,从左往右,用二进制位数上的数字乘以2的负位数次幂,然后把所有乘积相加即可得。
【例题】把二进制1.1101转化为十进制数。
解析:整数部分转化为十进制数是1 * 2^0 =1,
小数部分1 * 2^ -1 + 1 * 2^-2 + 0 * 2^-3 + 1 * 2^-4 =0.8125,
则二进制数1.1101对应的十进制数是1.8125。
十六进制转化为十进制
十六进制与十进制的对应关系:
- 十六进制:0 1 2 3 4 5 6 7 8 9 A B C D E F(字母不区分大小写)
- 十进制:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
- 十进制中的数位排列是这样的…… 万 千 百 十 个 十分 百分……
- 16进制中的数位排列是这样的…… 16^4 16^3 16^2 16^1 16^0 16^-1 16^-2 ……
【例题】2AF5换算成10进制。
5 * 16^0 + F * 16^1 + A * 16^2 + 2 * 16^3 =
5 * 16^0 + 15 * 16^1 + 10 * 16^2 + 2 * 16^3 = 10,997
十进制转化为二进制
1、整数转化为二进制数
十进制整数转换为二进制整数采用"除2取余,逆序排列"法。
具体做法是:用2整除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为小于1时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。

【例题】789=1100010101(B)
789/2=394 余1 第10位
394/2=197 余0 第9位
197/2=98 余1 第8位
98/2=49 余0 第7位
49/2=24 余1 第6位
24/2=12 余0 第5位
12/2=6 余0 第4位
6/2=3 余0 第3位
3/2=1 余1 第2位
1/2=0 余1 第1位
2、小数转化为二进制数
十进制小数转换成二进制小数采用"乘2取整,顺序排列"法。具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,此时0或1为二进制的最后一位。或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
【例题】0.625=(0.101)B
0.625 * 2=1.25 取出整数部分1
0.25 * 2=0.5 取出整数部分0
0.5 * 2=1 取出整数部分1
【例题】0.7=(0.1 0110 0110…)B
0.7 * 2=1.4 取出整数部分1
0.4 * 2=0.8 取出整数部分0
0.8 * 2=1.6 取出整数部分1
0.6 * 2=1.2 取出整数部分1
0.2 * 2=0.4 取出整数部分0
0.4 * 2=0.8 取出整数部分0
0.8 * 2=1.6 取出整数部分1
0.6 * 2=1.2 取出整数部分1
0.2 * 2=0.4 取出整数部分0
十进制转化为十六进制
与十进制转二进制类似;
对于整数部分,用被除数反复除以16,除第一次外,每次除以16均取前一次商的整数部分作被除数并依次记下每次的余数,直到商为小于1时为止;对于小数部分,采用连续乘以基数16,并依次取出的整数部分,直至结果的小数部分为0为止。
十六进制与十进制的对应关系:
- 十六进制:0 1 2 3 4 5 6 7 8 9 A B C D E F(字母不区分大小写)
- 十进制:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
【例题】十进制数23785转为十六进制。
第一步:23785/16=1486余9;
第二步:1486/16=92余14;
第三步:92/16=5余12;
第四步:5/16=0余5;
第五步:而十六进制中,10对应为a、11对应为b…15对应为f,再将余数倒写为5ce9;
二进制与十六进制互相转换、
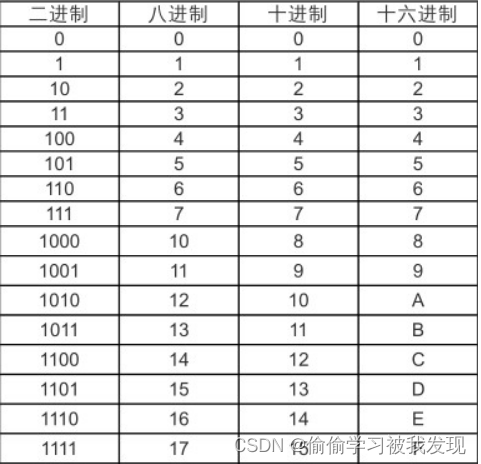
以小数点为分界点,小数点的位置不变,分整数转换和小数转换,一位十六进制对应四位二进制,不足则补0,凑够1比4的规律;
整数部分,从右到左每四位分开,不足四位时补0;
小数部分,从左到右每四位分开,不足四位时补0;
然后按一位十六进制对应四位二进制的规律进行转换,对换规律如上图所示;
【例题】二进制100101100转成十六进制。
先将二进制100101100从右到左每四位分开,不足四位时补0:
1 0010 1100 ----> 0001 0010 1100
然后按:一位十六进制对应四位二进制的规律进行转换,对换规律如上图所示;
所以:二进制100101100转成十六进制为:12C;
【例题】将二进制101011.101转换为十六进制。
首先,以小数点为分界点,小数点的位置不变;
然后,整数部分,101011,从右到左每四位分开,不足四位时补0:
10 1011 ----> 0010 1011;
其次,小数部分,101,从左到右每四位分开,不足四位时补0:
101 ----> 1010;
所以101011.101 ----> 0010 1011.1010;
最后转换,按一位十六进制对应四位二进制的规律进行转换,对换规律如上图所示;
101011.101 ----> 0010 1011.1010 的十六进制为:2B.A