大家好😃，我是想要慢慢变得优秀的向阳🌞同学👨‍💻，断更了整整一年，又开始恢复CSDN更新，从今天开始更新备战蓝桥30天系列，一共30天，如果对你有帮助或者正在备战蓝桥杯的小伙伴可以支持一下哦！~不能说肯定是干货，但会让你有所收获！💓💓💓

🍭 🍭 我们总是在生活扮演各种角色，却唯独很少扮演自己 🍭 🍭

奇数倍数 - 蓝桥云课 (lanqiao.cn)

思路：纯暴力模拟就行，填空题只要答案没什么好说的

public static void main(String[] args) {
        for (int i = 2; ; i++) {
            if (check(i * 2019)) {
                System.out.println(i * 2019);
                break;
            }
        }
    }

    public static boolean check(int n) {
        while (n != 0) {
            int tmp = n % 10;
            if (tmp % 2 == 0) return false;
            n /= 10;
        }
        return true;
    }

求值 - 蓝桥云课 (lanqiao.cn)

思路①：纯暴力模拟，因为数比较小，加上是一道填空题，考场遇到用的方法越简单越好
思路②：约数个数定理+唯一整数分解定理，一道数论题，相当于，已知约数个数，求对应的最小的自然数

思路①

//这段代码在idea跑着也挺费劲的，3秒左右出答案，但放在oj平台上肯定超时，我们只用System.out.println(45360);提交就行了
public static void main(String[] args) {

        for (int i = 1; ; i++) {
            int count = 0;
            for (int j = 1; j <= i; j++) {
                if(i % j == 0) count++;
                if (count == 100) {
                    System.out.println(i);//45360
                    return;
                }
            }
        }
    }

思路②

这道题本质其实是约数个数定理的逆用

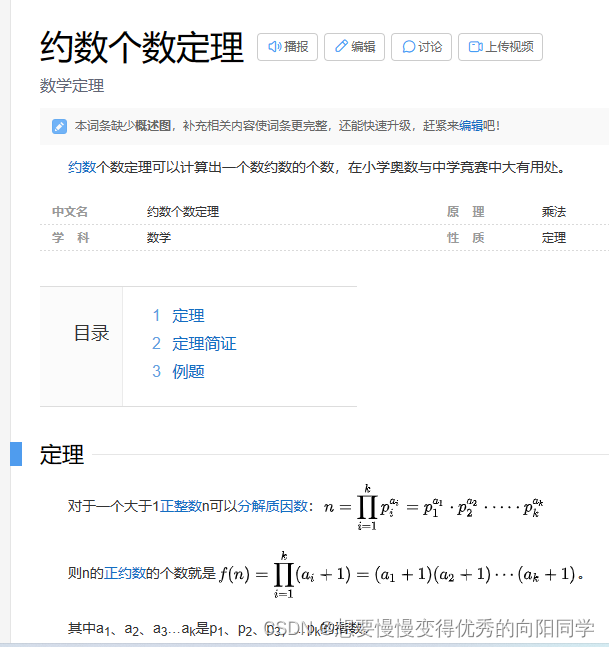
这个是百度定义的还有例题

例题：正整数378000共有多少个正约数？
解：将378000分解质因数378000=2^4×3^3×5^3×7^1//根据唯一整数分解定理我们知道任何一个整数都能拆成一堆质数的幂相乘，这里的质是2357
由约数个数定理可知378000共有正约数(4+1)×(3+1)×(3+1)×(1+1)=160个。//又根据约数个数定理，一个数的所有质因数数的幂+1之和相乘是这个数所有约数的之和

已知约数个数是100，100是根据约数个数定理，是正整数t（t是题目让我们求的值）的所有素因子的幂+1的和相乘得到的，那我们逆向思考可以得到，把10根据整数唯一分级定理拆成100=2*2*5*5，又因为求最小，把最小质数按顺序找到四个，分别是2345，把最大的幂给最小的质数（记得-1），答案就是2^(5-1)*3^(5-1)*5^(2-1)*7^(2-1)，得到最小的自然数

求和 - 蓝桥云课 (lanqiao.cn)

思路：前缀和，看S的表达式，会发现如果提取一个公因数那么S=a1*(a2+a3..an)+a2*(a3+..an)...这样思路一下子就清晰起来了，括号里面的数据就是在暗示我们用前缀和

//因为这道题输入数据达到200000，蓝桥比赛是IO赛制的比赛，提交根本不知道对不对，可能有数据太大超时了，为了稳妥
//避免这种情况可能的发生，我们这里使用了快读，虽然说正常的输入输出也能过，但如果真正的比赛你是不清楚的，稳一点总是好的
public static void main(String[] args) throws IOException {
        long ans = 0;
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] s = br.readLine().split(" ");
        int n = Integer.parseInt(s[0]);
        s = br.readLine().split(" ");
        for (int i = 1; i <= n; i++) {
            a[i] = Integer.parseInt(s[i - 1]);
        }
        for (int i = 1; i <= n; i++) {
            a[i] += a[i - 1];
        }
        for (int i = 1; i <= n; i++) {
            //这里写的有点复杂其实就是a[1]*(a[2]+a[3]..a[n])因为是前缀和数组，a[1]表达起来有点费劲
            //当然这道题甚至可以不用专门再写个前缀和循环了，因为是从头到尾遍历了，直接用一个sum变量来接受更加简单
            //long sum = 0;
            //for (int i = 0; i < n; i++) {
            //ans+=a[i]*sum;
            //sum+=a[i];
            //}
            ans += (long) (a[i] - a[i - 1]) * (a[n] - a[i]);
        }
        System.out.println(ans);
    }