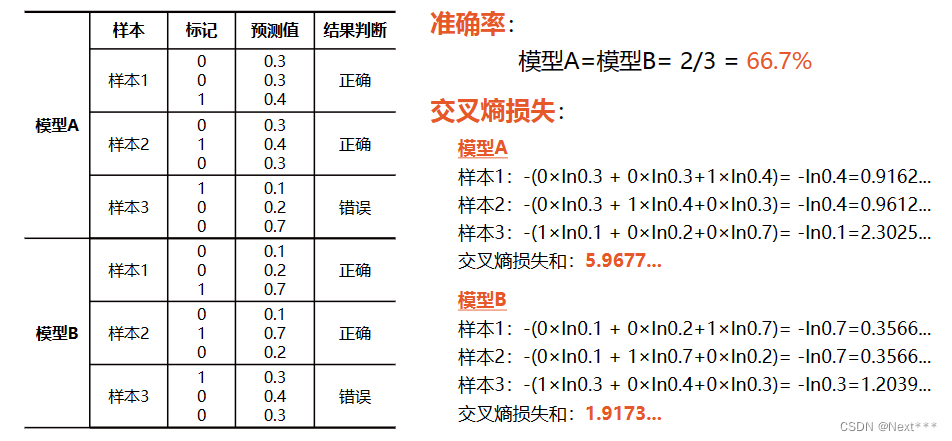
解释：将图像映射成图，以图为研究对象，利用图的理论知识获得图像的分割。

下面介绍：图的基本理论，基于图论的归一化分割算法

一、图的基本理论

图G＝（V，E，），分别是：节点、边、顶点和边的对应关系。简单记为G＝（V，E）。

图的几个基本概念

1.顶点的度【无向图、有向图(入度、出度)
2.连通图【无向图(有路径)、有向图(任意两点之间连通)
3.子图和割【补图(V1∪V2=V，则图G1和G2互为补图)、割集(如果将图G分为两个互不相交的子图，我们称连接两个子图的边的集合为割集)

割集S是一个边集:如果在图G中去掉边集S中所有的边，则图G就变成一个二分支的分离图。
割集的边的权重之和叫做割:

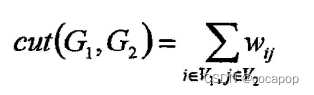
 图像与图的映射关系

图像的像素《——》图的顶点V
图像的相邻像素《——》图的边E
相邻像素间的相似度《——》图的权值W

图像构造图的过程

步骤：(1)节点的选取与边的连接
节点的选取分为：一对一(每个像素对应图的一个节点)、多对一(多像素对应一节点，超像素)
边的连接方式(像素间的邻接关系)：4邻接、8邻接(常用这个作为标准的像素邻接关系)、不太常用的全连接(任何像素都与图像中的其他所有像素连边，增加算法复杂性了)、固定区域内的全连接(以某个像素为中心，限定某个固定半径区域内的像素全部连边)

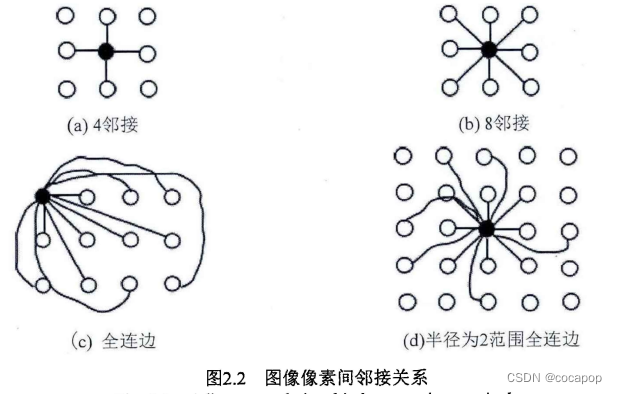
（2）权重的选择 

边上的权重反应像素间的相似性或差异性。度量两个节点间颜色、亮度、距离、纹理等方面
常见的计算函数：

第一种：

 第二种：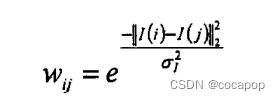

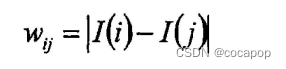
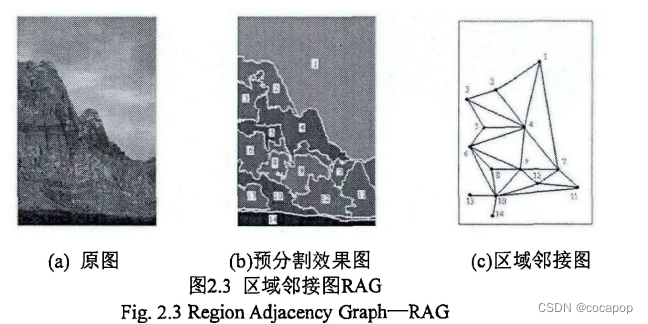
 （3）区域邻接图(RAG)

 选多个像素组成的区域映射为一个节点，两邻域区域建立连接边。

 基于图论的分割算法

他们主要是围绕着分割准则进行分割。
介绍几个代表性的分割准则：
（1）基于特征向量的分割准则——类似于权重的矩阵对角化。构造目标函数并当其取最大值时，各元素之间具有很大相似度，属于该类的可能性大，从而达到分类目的。
（2）基于区域合并的分割准则——设计了一种预测两个区域块之间是否能产生边界的法则，这个法则产生的分割可以达到全局最优
（3）基于归一化分割的准则Ncuts——将整幅图分成两部分，然后每一步都把其中一个部分继续再分成两部分，直到达到某种条件再停止分割。

二、归一化分割算法

算法基本原理

定义一个将图分成两部分的目标函数：

 Wu和Leahy提出的基于最小割准则的聚类方法：求上面目标函数cut（A，B）的最小值，就得到了图的最优分割。递归调用这个最小割准则可以将一幅图一直二分下去，最终得到满意的结果。但是最小割准则会把一些孤立的点分割为独立的一类，这样最小割准则会失去意义的。

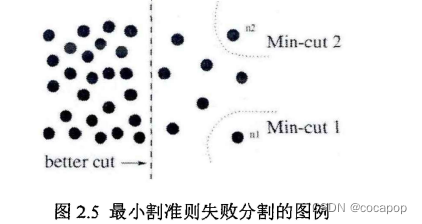
 为了弥补这个最小割的“偏见”，Shi和Malik提出归一化分割方法。它定义了一个新的准则来衡量A，B间的相似度。

 

 归一化分割的求解

（数学公式推导）

 

 归一化分割结果

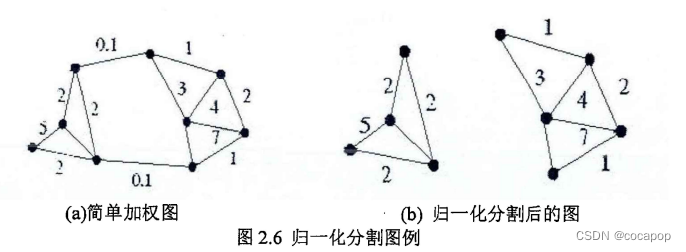
归一化分割实现方式

（1）递归调用二分归一化分割 
缺点：只利用了第二小特征值对应的特征向量，舍弃了其他的特征向量。其他特征向量也包含了有用的分割信息。

（2）多分归一化分割
改进的地方：取前n个特征向量作为每个像素的n维指标向量。
步骤：先用K-means聚类算法将图像过分割成k类，然后使用下面两种方法处理：