Lesson11---分类问题

11.1 逻辑回归

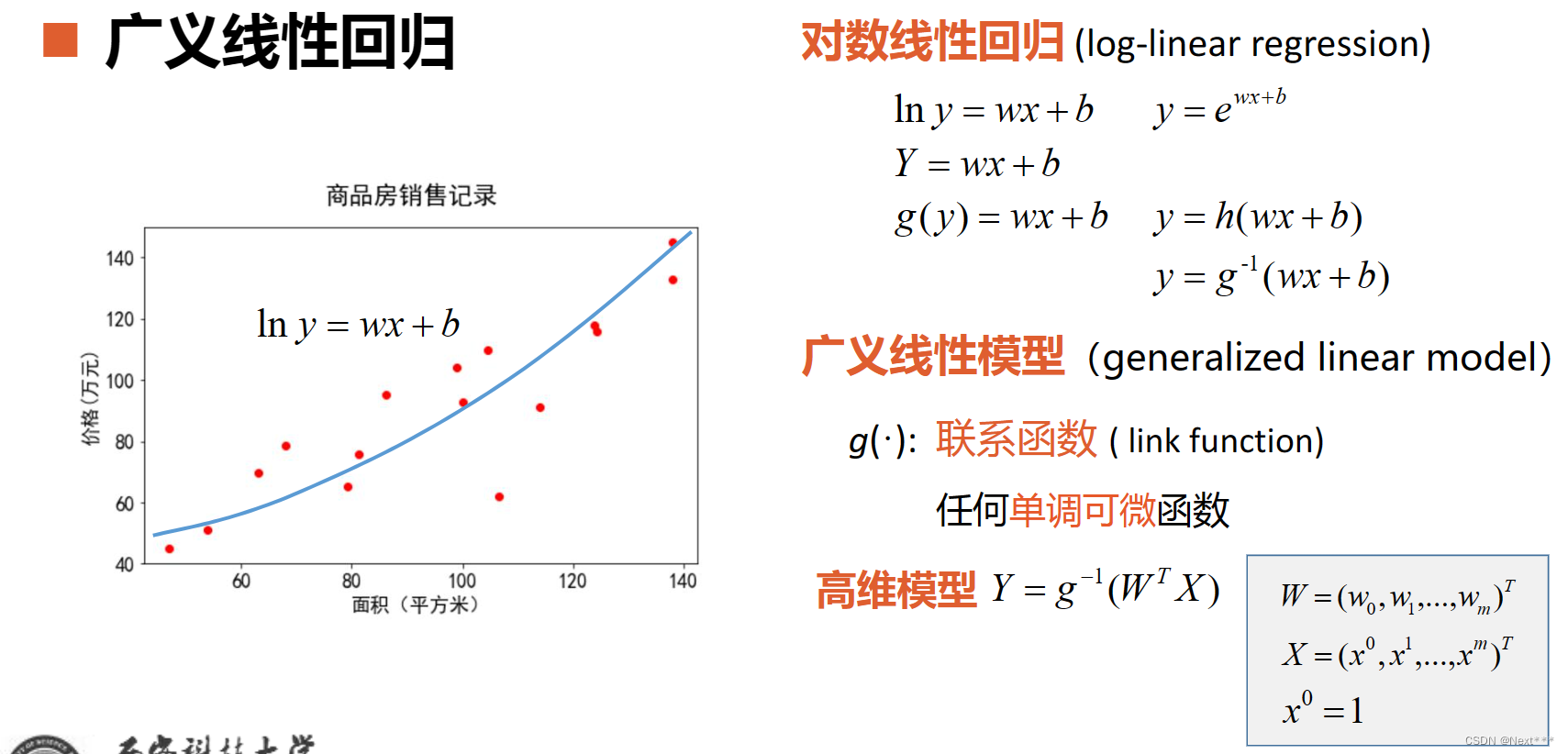
11.1.1 广义线性回归

课程回顾

线性回归：将自变量和因变量之间的关系，用线性模型来表示；根据已知的样本数据，对未来的、或者未知的数据进行估计

11.1.2 逻辑回归

11.1.2.1 分类问题

分类问题：垃圾邮件识别，图片分类，疾病判断
分类器：能偶自动对输入的数据进行分类
输入：特征；输出：离散值

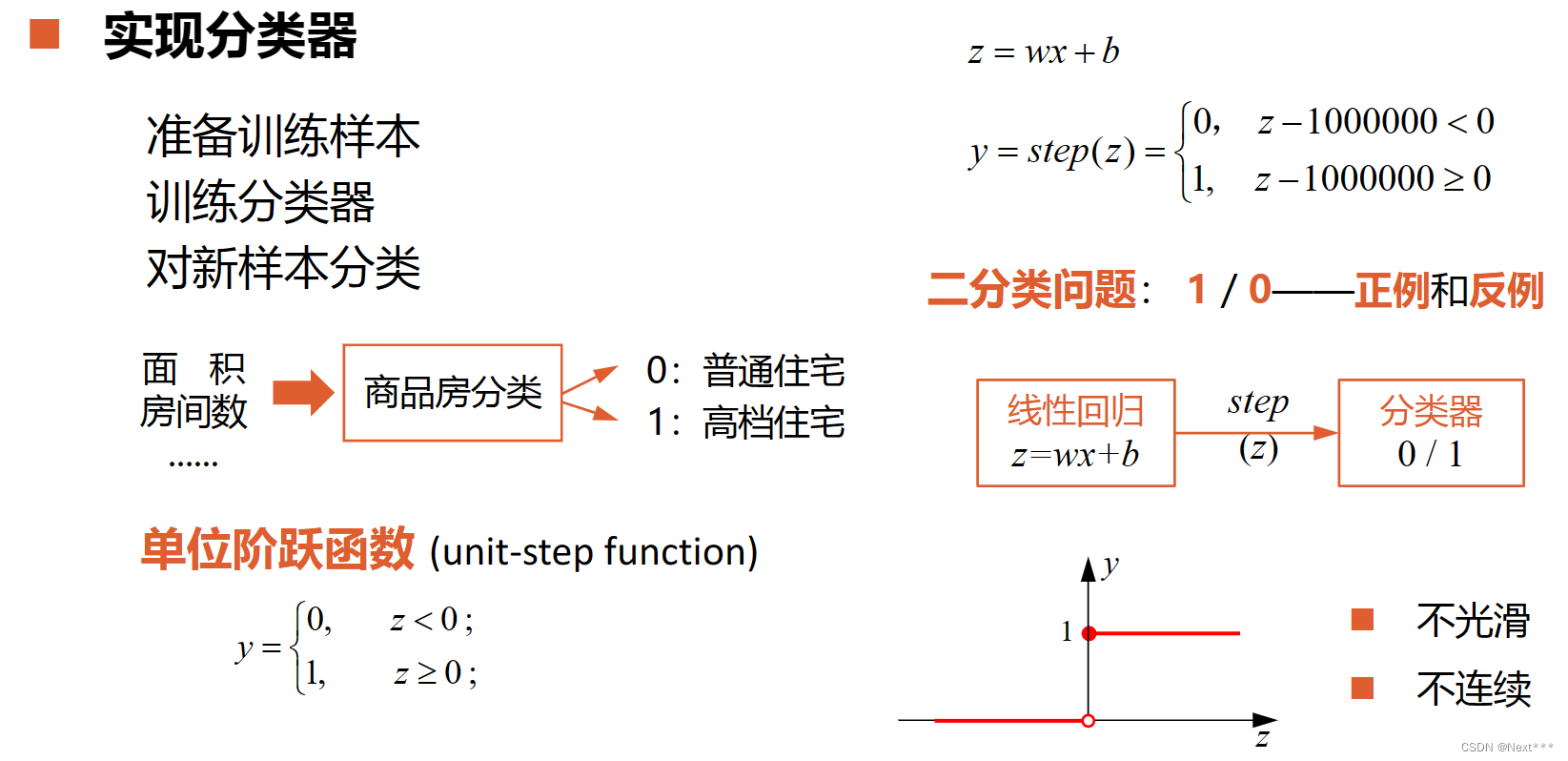
11.1.2.2 实现分类器

准备训练样本
训练分类器
对新样本分类
单位阶跃函数（unit-step function）
不光滑
不连续
二分类问题 1/0–正例和反例
对数几率函数（logistic function）: $y=1/(1+e^{-z})$
单调上升，连续，光滑
任意阶可导
对数几率回归/逻辑回归（logistic regression）： $y=1/（1+e^{-(wx+b)}）$
Sigmoid函数：形状s的函数，能够将取值范围无穷大的函数转化为一个0到1范围的值；
$y=g^{-1}(z)=σ(z)=σ(wx+b)=1/(1+e^{-z})=1/(1+e^{-(wx+b)})$
多元模型
$y = 1/(1+e^{-(W^TX)})$
$W = (w_{0},w_{1},…,w_{m})^{T}$
$X = (x_{0},x_{1},…,x_{m})^{T}$
$x^{0}=1$

在这里插入图片描述

11.1.3 交叉熵损失函数

交叉熵损失函数

每一项误差都是非负的
函数值和误差的变化趋势一致
凸函数
对模型参数求偏导数，无σ’()项

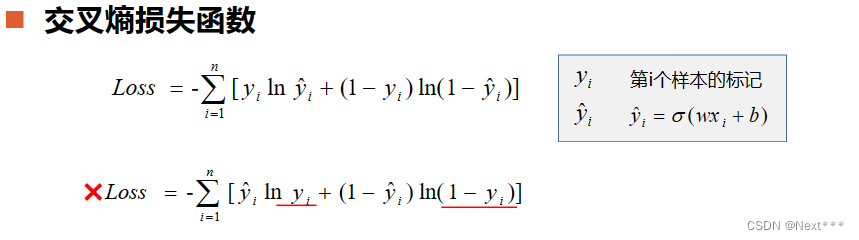
在这里插入图片描述

平均交叉熵损失函数

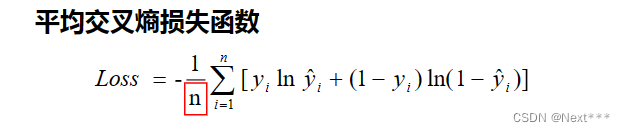
在这里插入图片描述

偏导数的值只受到标签值和预测值偏差的影响
交叉熵损失函数是凸函数，因此使用梯度下降法得到的极小值就是全局最小值

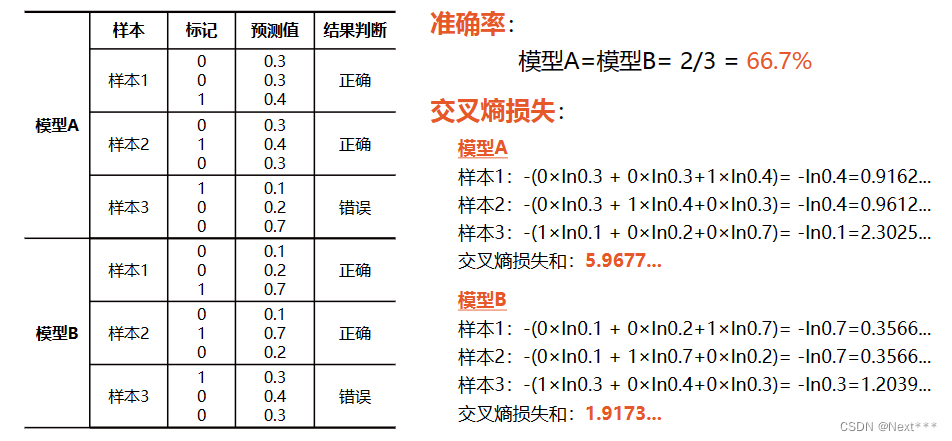
11.1.4 准确率（accuracy）

可以使用准确率来评价一个分类器性能
准确率=正确分类的样本数/总样本数
仅仅通过准确率是无法细分出模型分类器的优劣的

11.1.5 手推三分类问题-交叉熵损失函数，权值更新公式

11.2 实例：实现一元逻辑回归

11.2.1 sigmoid()函数-代码实现

$y = 1 / ( 1 + e^{-(wx+b)})$

>>> import tensorflow as tf
>>> import numpy as np
>>> x = np.array([1.,2.,3.,4.])
>>> w = tf.Variable(1.)
>>> b = tf.Variable(1.)
>>> y = 1/(1+tf.exp(-(w*x+b)))
>>> y
<tf.Tensor: id=46, shape=(4,), dtype=float32, numpy=array([0.880797  , 0.95257413, 0.98201376, 0.9933072 ], dtype=float32)>

注意tf.exp()函数的参数要求是浮点数，否则会报错

11.2.2 交叉熵损失函数-代码实现

在这里插入图片描述

>>> import tensorflow as tf
>>> import numpy as np

>>> y = np.array([0,0,1,1])
>>> pred=np.array([0.1,0.2,0.8,0.49])

>>> # 交叉熵损失函数
>>> -tf.reduce_sum(y*tf.math.log(pred)+(1-y)*tf.math.log(1-pred))
<tf.Tensor: id=58, shape=(), dtype=float64, numpy=1.2649975061637104>

>>> # 平均交叉熵巡损失函数
>>> -tf.reduce_mean(y*tf.math.log(pred)+(1-y)*tf.math.log(1-pred)) 
<tf.Tensor: id=70, shape=(), dtype=float64, numpy=0.3162493765409276>

11.2.3 准确率-代码实现

11.2.3.1 判断阈值是0.5-tf.round()函数

准确率=正确分类的样本数/总样本数

>>> import tensorflow as tf
>>> import numpy as np

>>> y = np.array([0,0,1,1])
>>> pred=np.array([0.1,0.2,0.8,0.49])

>>> # 如果将阈值设为0.5，可以使用四舍五入函数round()将其转换为0或1 
>>> tf.round(pred)
<tf.Tensor: id=83, shape=(4,), dtype=float64, numpy=array([0., 0., 
1., 0.])>

>>> # 然后使用equal()函数逐元素比较预测值和标签值，得到的结果是一个
和y形状相同的一维张量
>>> tf.equal(tf.round(pred),y)
<tf.Tensor: id=87, shape=(4,), dtype=bool, numpy=array([ True,  True,  True, False])>

>>> # 下面使用cast()函数把这个结果转化为整数
>>> tf.cast(tf.equal(tf.round(pred),y),tf.int8)
<tf.Tensor: id=92, shape=(4,), dtype=int8, numpy=array([1, 1, 1, 0], dtype=int8)>

>>> # 然后对所有的元素求平均值，就是得到正确样本在所有样本中的比例 
>>> tf.reduce_mean(tf.cast(tf.equal(tf.round(pred),y),tf.int8))    
<tf.Tensor: id=99, shape=(), dtype=int8, numpy=0>

>>> # 记得，如果round()函数，参数是0.5，返回的值是0
>>> tf.round(0.5)
<tf.Tensor: id=101, shape=(), dtype=float32, numpy=0.0>

11.2.3.2 判断阈值不是0.5–where(condition,a,b)函数

where(condition,a,b)

根据条件condition返回a或者b的值
如果condition中的某个元素为真，对应位置返回a，否则返回b

>>> import tensorflow as tf
>>> import numpy as np

>>> y = np.array([0,0,1,1])
>>> pred=np.array([0.1,0.2,0.8,0.49])

>>> tf.where(pred<0.5,0,1)
<tf.Tensor: id=105, shape=(4,), dtype=int32, numpy=array([0, 0, 1, 
0])>

>>> pred<0.5
array([ True,  True, False,  True])

>>> tf.where(pred<0.4,0,1)

参数a和b还可以是数组或者张量，这时，a和b必须有相同的形状，并且他们的第一维必须和condition形状一致

>>> import tensorflow as tf
>>> import numpy as np

>>> pred=np.array([0.1,0.2,0.8,0.49])

>>> a = np.array([1,2,3,4])
>>> b = np.array([10,20,30,40])

>>> # 当pred中的元素小于0.5时，就返回a中对应位置的元素，否则，返回b中对应位置的元素
>>> tf.where(pred<0.5,a,b)
<tf.Tensor: id=117, shape=(4,), dtype=int32, numpy=array([ 1,  2, 30,  4])>
>>> # 可以看到数组pred中1、2、4个元素都小于0.5，因此取数组a中的元素
，而第3个元素大于0.5，取b中的元素

参数a和b也可以省略，这时的返回值数组pred中大于等于0.5的元素的索引，返回值以一个二维张量的形式给出

>>> tf.where(pred>=0.5)
<tf.Tensor: id=119, shape=(1, 1), dtype=int64, numpy=array([[2]], dtype=int64)>

下面使用where计算准确率

>>> import tensorflow as tf
>>> import numpy as np
>>> y = np.array([0,0,1,1]) 
>>> pred=np.array([0.1,0.2,0.8,0.49])  

>>> tf.reduce_mean(tf.cast(tf.equal(tf.where(pred<0.5,0,1),y),tf.float32))
<tf.Tensor: id=136, shape=(), dtype=float32, numpy=0.75>

11.2.4 一元逻辑回归-房屋销售记录实例

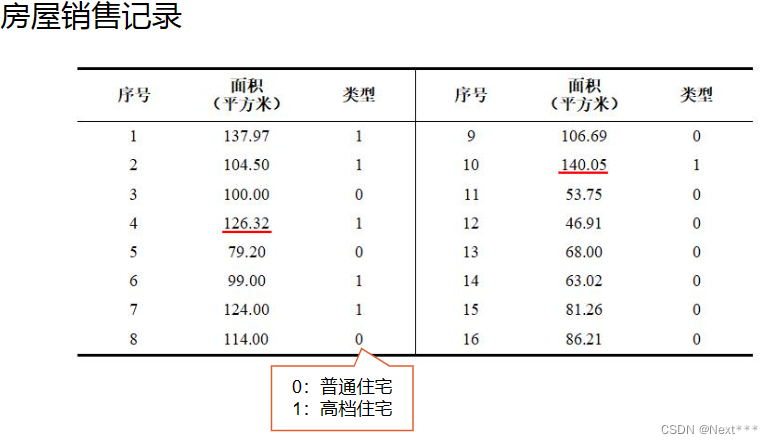
在这里插入图片描述

11.2.4.1 加载数据

# 1 加载数据
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# 面积
x = np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
# 类型
y = np.array([1,1,0,1,0,1,1,0,0,1,0,0,0,0,0,0])

plt.scatter(x,y)
plt.show()

输出结果为：
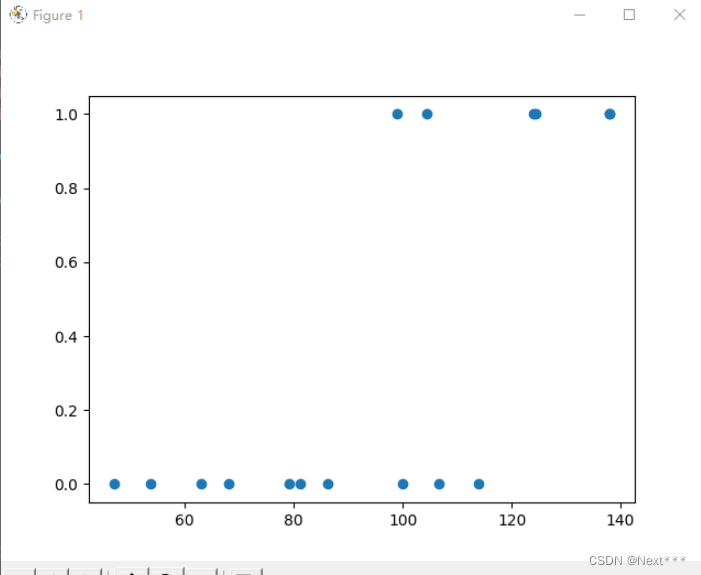
在这里插入图片描述

类别只有0和1两种

11.2.4.2 数据处理

# 2 数据处理
# sigmoid函数是以0点为中心的，所以对数据中心化
x_train = x - np.mean(x)
y_train = y

plt.scatter(x_train,y_train)
plt.show()

输出结果为：
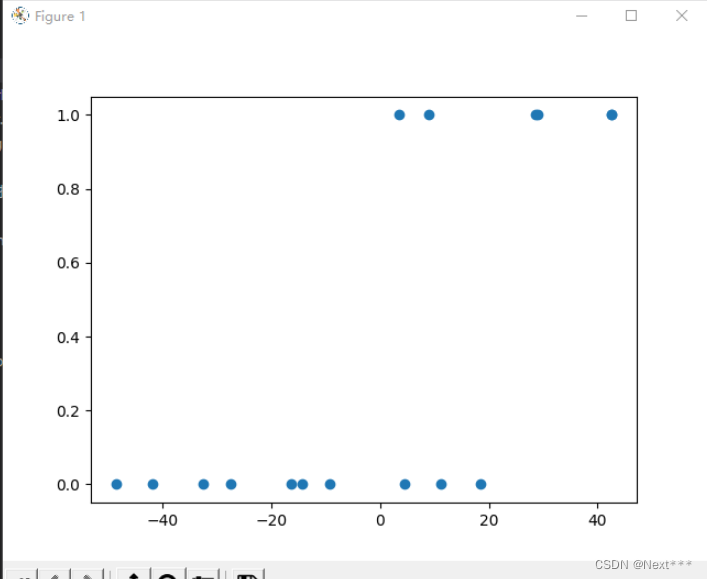
在这里插入图片描述

可以看到，这些点整体平移，这些点相对位置不变

11.2.4.3 设置超参数

# 3 设置超参数
learn_rate = 0.005
iter = 5
display_step = 1

11.2.4.4 设置模型变量初始值

# 4 设置模型变量初始值
np.random.seed(612)
w = tf.Variable(np.random.randn())
b = tf.Variable(np.random.randn())

11.2.4.5 训练模型

# 5 训练模型
cross_train = []
acc_train = []

for i in range(0,iter+1):

    with tf.GradientTape() as tape:
        pred_train = 1/(1+tf.exp(-w*x_train+b))
        Loss_train = -tf.reduce_mean(y_train*tf.math.log(pred_train)+(1-y_train)*tf.math.log(1-pred_train))
        Accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(pred_train<0.5,0,1),y_train),tf.float32))

    cross_train.append(Loss_train)
    acc_train.append(Accuracy_train)

    dL_dw,dL_db = tape.gradient(Loss_train,[w,b])

    w.assign_sub(learn_rate*dL_dw)
    b.assign_sub(learn_rate*dL_db)

    if i % display_step == 0:
        print("i: %i, Train Loss: %f, Accuracy: %f" % (i,Loss_train,Accuracy_train))

输出结果为：

i: 0, Train Loss: 1.140986, Accuracy: 0.375000
i: 1, Train Loss: 0.703207, Accuracy: 0.625000
i: 2, Train Loss: 0.648479, Accuracy: 0.625000
i: 3, Train Loss: 0.631729, Accuracy: 0.687500
i: 4, Train Loss: 0.624276, Accuracy: 0.687500
i: 5, Train Loss: 0.620331, Accuracy: 0.750000

11.2.4.6 增加sigmoid曲线可视化输出

# 1 加载数据
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# 面积
x = np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
# 类型
y = np.array([1,1,0,1,0,1,1,0,0,1,0,0,0,0,0,0])

# 2 数据处理
# sigmoid函数是以0点为中心的，所以对数据中心化
x_train = x - np.mean(x)
y_train = y

# 3 设置超参数
learn_rate = 0.005
iter = 5
display_step = 1

# 4 设置模型变量初始值
np.random.seed(612)
w = tf.Variable(np.random.randn())
b = tf.Variable(np.random.randn())

x_ = range(-80,80)
y_ = 1/(1+tf.exp(-(w*x_+b)))

# 迭代之前，输出数据的散点图
plt.scatter(x_train,y_train)
# 使用初始化参数时的sigmoid曲线
plt.plot(x_,y_,c='r',linewidth=3)

# 5 训练模型
cross_train = []
acc_train = []

for i in range(0,iter+1):

    with tf.GradientTape() as tape:
        pred_train = 1/(1+tf.exp(-w*x_train+b))
        Loss_train = -tf.reduce_mean(y_train*tf.math.log(pred_train)+(1-y_train)*tf.math.log(1-pred_train))
        Accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(pred_train<0.5,0,1),y_train),tf.float32))

    cross_train.append(Loss_train)
    acc_train.append(Accuracy_train)

    dL_dw,dL_db = tape.gradient(Loss_train,[w,b])

    w.assign_sub(learn_rate*dL_dw)
    b.assign_sub(learn_rate*dL_db)

    if i % display_step == 0:
        print("i: %i, Train Loss: %f, Accuracy: %f" % (i,Loss_train,Accuracy_train))
        y_ = 1/(1+tf.exp(-(w*x_+b)))
        plt.plot(x_,y_)
        # 输出当前权值时的sigmoid曲线
plt.show()

输出结果为：

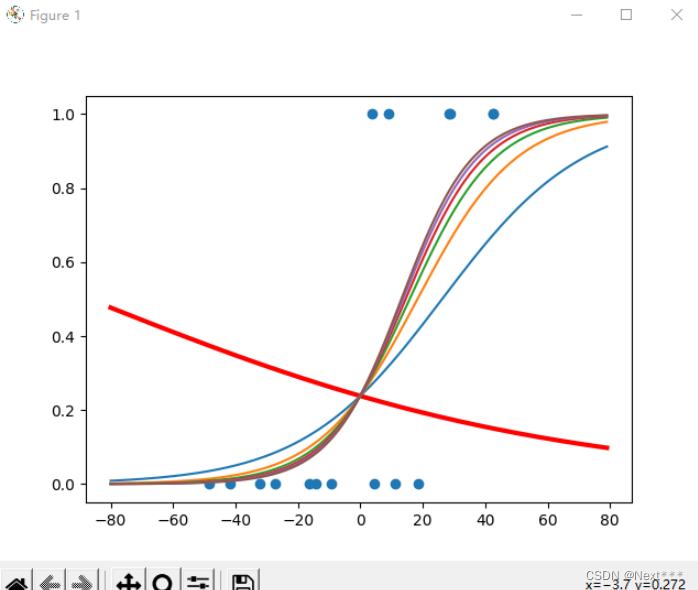
在这里插入图片描述

红色是使用初始参数时的sigmoid曲线，虽然看起来很离谱，但是恰好属于普通住宅的这10个样本的概率都在0.5以下，所以分类正确率为10/16
蓝色是第一次迭代结果
紫色是最后一次迭代的结果
在0-20之间，出现一段的重合，有一定的交集，所以这个区域中的点可能会出现分类错误，导致准确率无法达到100
第一次分类的结果，虽然正确率更大，但是从整体来看，还是经过更多次迭代之后更加合理

11.2.4.7 验证模型

x_test = [128.15,45.00,141.43,106.27,99.00,53.84,85.36,70.00,162.00,114.60]
pred_test = 1/(1+tf.exp(-(w*(x_test-np.mean(x))+b)))
y_test = tf.where(pred_test<0.5,0,1)
for i in range(len(x_test)):
    print(x_test[i],"\t",pred_test[i].numpy(),"\t",y_test[i].numpy(),"\t")

输出结果为：

128.15   0.84752923      1 
45.0     0.003775026     0
141.43   0.94683856      1
106.27   0.4493811       0
99.0     0.30140132      0
53.84    0.008159011     0
85.36    0.11540905      0
70.0     0.032816157     0
162.0    0.99083763      1
114.6    0.62883806      1

11.2.4.8 预测值的sigmoid曲线和散点图

# 1 加载数据
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# 面积
x = np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
# 类型
y = np.array([1,1,0,1,0,1,1,0,0,1,0,0,0,0,0,0])

# 2 数据处理
# sigmoid函数是以0点为中心的，所以对数据中心化
x_train = x - np.mean(x)
y_train = y

# 3 设置超参数
learn_rate = 0.005
iter = 5
display_step = 1

# 4 设置模型变量初始值
np.random.seed(612)
w = tf.Variable(np.random.randn())
b = tf.Variable(np.random.randn())

#x_ = range(-80,80)
#y_ = 1/(1+tf.exp(-(w*x_+b)))

# 迭代之前，输出数据的散点图
#plt.scatter(x_train,y_train)
# 使用输出参数时的sigmoid曲线
#plt.plot(x_,y_,c='r',linewidth=3)

# 5 训练模型
cross_train = []
acc_train = []

for i in range(0,iter+1):

    with tf.GradientTape() as tape:
        pred_train = 1/(1+tf.exp(-w*x_train+b))
        Loss_train = -tf.reduce_mean(y_train*tf.math.log(pred_train)+(1-y_train)*tf.math.log(1-pred_train))
        Accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(pred_train<0.5,0,1),y_train),tf.float32))

    cross_train.append(Loss_train)
    acc_train.append(Accuracy_train)

    dL_dw,dL_db = tape.gradient(Loss_train,[w,b])

    w.assign_sub(learn_rate*dL_dw)
    b.assign_sub(learn_rate*dL_db)

    if i % display_step == 0:
        print("i: %i, Train Loss: %f, Accuracy: %f" % (i,Loss_train,Accuracy_train))
        #y_ = 1/(1+tf.exp(-(w*x_+b)))
        #plt.plot(x_,y_)
# 虽然使用x_test表示，但是它们不是测试集，测试集是有标签的数据
x_test = [128.15,45.00,141.43,106.27,99.00,53.84,85.36,70.00,162.00,114.60]
pred_test = 1/(1+tf.exp(-(w*(x_test-np.mean(x))+b)))
y_test = tf.where(pred_test<0.5,0,1)
for i in range(len(x_test)):
    print(x_test[i],"\t",pred_test[i].numpy(),"\t",y_test[i].numpy(),"\t")

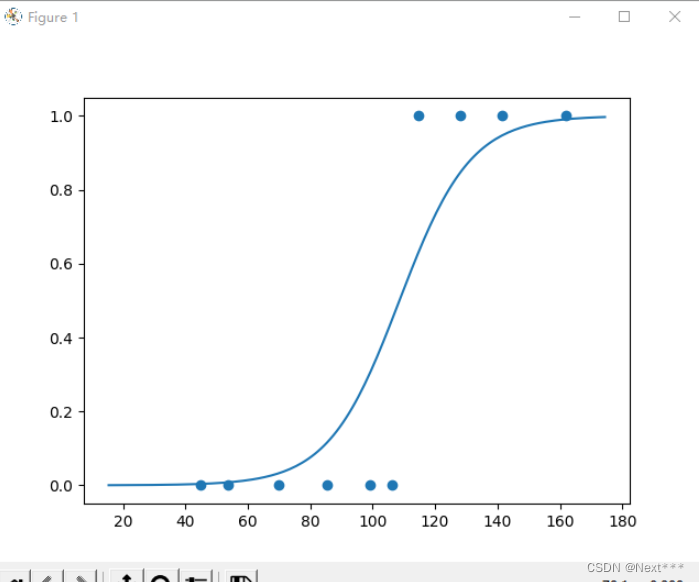
plt.scatter(x_test,y_test)

x_ = range(-80,80)
y_ = 1/(1+tf.exp(-(w*x_+b)))
plt.plot(x_+np.mean(x),y_)

plt.show()

输出结果为:
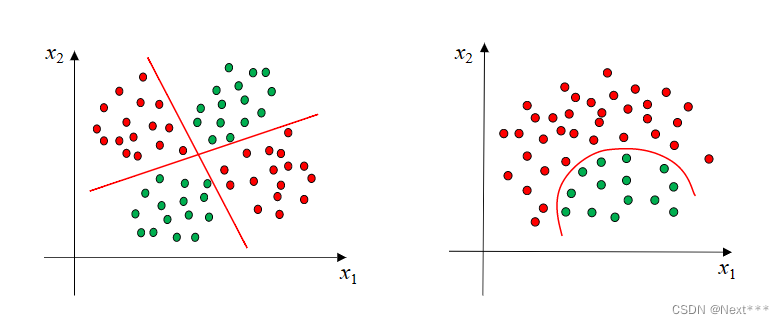
在这里插入图片描述

11.3 线性分类器（Linear Classifier）

11.3.1 决策边界-线性可分

二维空间中的数据集，如果可以被一条直线分为两类，我们称之为线性可分数据集，这条直线就是一个线性分类器
在三维空间中，如果数据集线性可分，是指被一个平面分为两类
在一维空间中，所有的点都在一条直线上，线性可分可以理解为可以被一个点分开
这里的，分类直线、平面、点被称为决策边界
一个m维数据集，
如果可以被一个超平面一分为二，那么这个数据集就是线性可分的，这个超平面就是决策边界

11.3.2 线性不可分

线性不可分：样本得两条直线分开，或者一条曲线分开

11.3.3 逻辑运算

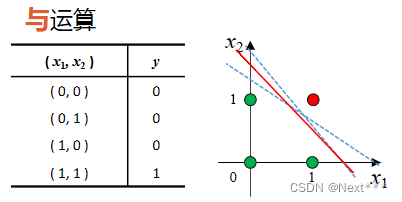
11.3.3.1 线性可分-与、或、非

在逻辑运算中，与&、或|、非！都是线性可分的
显然可以通过训练得到对应的分类器，并且一定收敛
与运算
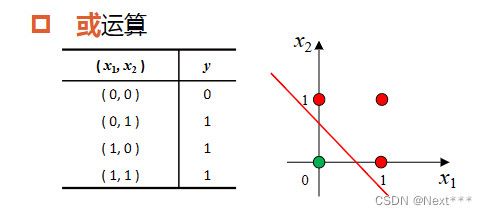
或运算
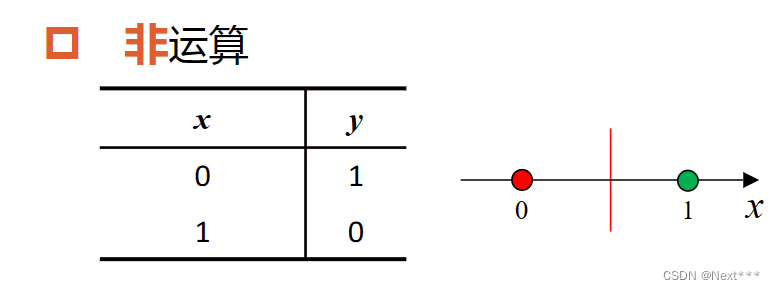
非运算

11.3.3.2 线性不可分-异或

异或运算，也可以看作是按类加运算

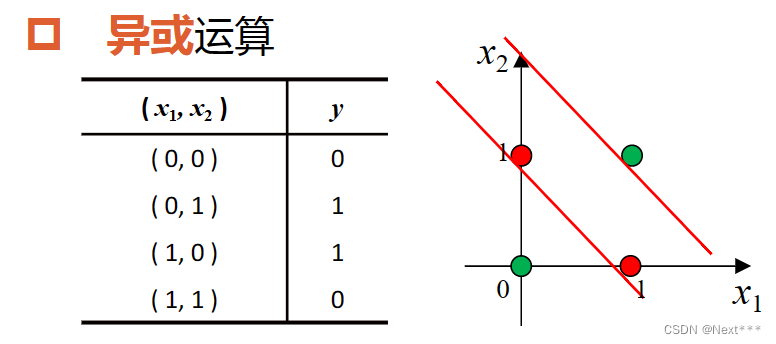
在这里插入图片描述

显然，要分开它，最少得两条直线

11.4 实例：实现多元逻辑回归

11.4.1 实现多元逻辑回归

11.4.1.1 鸢尾花数据集（iris）再次介绍

在这里，使用逻辑回归实现对鸢尾花（iris）的分类
Iris数据集

150个样本
4个属性：花萼长度（Sepal Length）、花萼宽度（Sepal Width）、花瓣长度（Petal Length）、花瓣宽度（Petal Width）
1个标签：山鸢尾（Setosa）、变色鸢尾（Versicolour）、维吉尼亚鸢尾（Virginica）
属性两两可视化后的结果为：

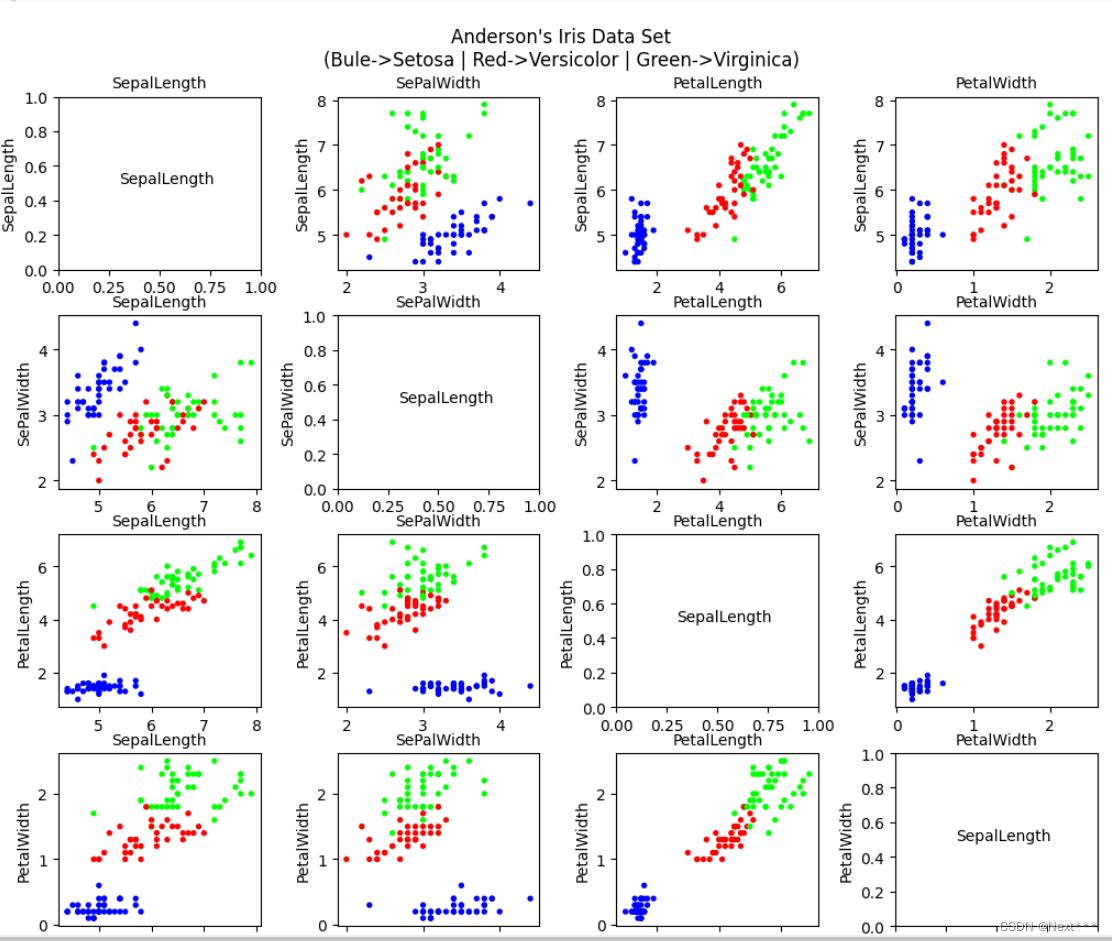
山鸢尾（蓝色）、变色鸢尾（红色）、维吉尼亚鸢尾（绿色）

蓝色的与其他两个差别大，选择任何两个都可以区分开；所以选择蓝色（山鸢尾）的和红色（变色鸢尾）两种鸢尾花，花萼长度和花萼宽度两种属性，通过逻辑回归实现对他们的分类
了解鸢尾花数据集的具体使用方法可以参考Lesson6—Matplotlib数据可视化中的6.5节

11.4.1.2 实现多元逻辑回归

11.4.1.2.1 加载数据

# 1 加载数据
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)

df_iris = pd.read_csv(train_path,header=0) # 是一个pandas二维数据表

11.4.1.2.2 处理数据

11.4.1.2.2.1 自己定义色彩方案mpl.colors.ListedColormap()

11.4.1.2.2.2 无须归一化，只需中心化

# 2 处理数据
# 首先将二维数据表转化为numpy数组
iris= np.array(df_iris)  # shape(120,5)

# 提取属性和标签
train_x = iris[:,0:2]  # （120，2）
train_y = iris[:,4] # （120，）

# 提取山鸢尾和变色鸢尾，提取出标签纸为0和1的值
x_train = train_x[train_y < 2] # (78,2)
y_train = train_y[train_y < 2] # (78,)

# 记录现在的样本数
num = len(x_train)
# 中心化处理
x_train = x_train - np.mean(x_train,axis= 0)

# 生成多元模型的属性矩阵和标签列向量
x0_train = np.ones(num).reshape(-1,1)
X = tf.cast(tf.concat((x0_train,x_train),axis=1),tf.float32) # shape(78,3)
Y = tf.cast(y_train.reshape(-1,1),tf.float32) # shape(78,1)
# 可视化样本
#cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案
#plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
#plt.show()

处理结果为：

在这里插入图片描述

可以看到中心化之后，样本点被平移，样本点的横坐标和纵坐标都是0

11.4.1.2.3 设置超参数

# 3 设置超参数
learn_rate = 0.2 
iter = 120
display_step = 30

11.4.1.2.4 设置模型参数初始值

# 4 设置模型参数初始值
np.random.seed(612)
W = tf.Variable(np.random.randn(3,1),dtype=tf.float32)

11.4.1.2.5 训练模型

# 5 训练模型
ce = []
acc = []

for i in range(0,iter+1):
    with tf.GradientTape() as tape:
        PRED = 1/(1+tf.exp(-tf.matmul(X,W))) # 每个样本的预测概率
        Loss = -tf.reduce_mean(Y*tf.math.log(PRED)+(1-Y)*tf.math.log(1-PRED))

    accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED.numpy()<0.5,0.,1.),Y),tf.float32))
    ce.append(Loss)
    acc.append(accuracy)

    dL_dW = tape.gradient(Loss,W)
    W.assign_sub(learn_rate*dL_dW)

    if i % display_step ==0:
        print("i: %i, Acc: %f, Loss: %f" % (i,accuracy,Loss))

输出结果为：

i: 0, Acc: 0.230769, Loss: 0.994269
i: 30, Acc: 0.961538, Loss: 0.481892
i: 60, Acc: 0.987179, Loss: 0.319128
i: 90, Acc: 0.987179, Loss: 0.246626
i: 120, Acc: 1.000000, Loss: 0.204982

11.4.1.2.6 代码汇总（包含前五个步骤）

# 1 加载数据
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)

df_iris = pd.read_csv(train_path,header=0) # 是一个pandas二维数据表

# 2 处理数据
# 首先将二维数据表转化为numpy数组
iris= np.array(df_iris)  # shape(120,5)

# 提取属性和标签
train_x = iris[:,0:2]  # （120，2）
train_y = iris[:,4] # （120，）

# 提取山鸢尾和变色鸢尾，提取出标签纸为0和1的值
x_train = train_x[train_y < 2] # (78,2)
y_train = train_y[train_y < 2] # (78,)

# 记录现在的样本数
num = len(x_train)
# 中心化处理
x_train = x_train - np.mean(x_train,axis= 0)

# 生成多元模型的属性矩阵和标签列向量
x0_train = np.ones(num).reshape(-1,1)
X = tf.cast(tf.concat((x0_train,x_train),axis=1),tf.float32) # shape(78,3)
Y = tf.cast(y_train.reshape(-1,1),tf.float32) # shape(78,1)
# 可视化样本
#cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案
#plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
#plt.show()

# 3 设置超参数
learn_rate = 0.2 
iter = 120
display_step = 30

# 4 设置模型参数初始值
np.random.seed(612)
W = tf.Variable(np.random.randn(3,1),dtype=tf.float32)

# 5 训练模型
ce = []
acc = []

for i in range(0,iter+1):
    with tf.GradientTape() as tape:
        PRED = 1/(1+tf.exp(-tf.matmul(X,W))) # 每个样本的预测概率
        Loss = -tf.reduce_mean(Y*tf.math.log(PRED)+(1-Y)*tf.math.log(1-PRED))

    accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED.numpy()<0.5,0.,1.),Y),tf.float32))
    ce.append(Loss)
    acc.append(accuracy)

    dL_dW = tape.gradient(Loss,W)
    W.assign_sub(learn_rate*dL_dW)

    if i % display_step ==0:
        print("i: %i, Acc: %f, Loss: %f" % (i,accuracy,Loss))

11.4.1.2.6 可视化

11.4.1.2.6.1 绘制损失和准确率变化曲线

# 损失和准确率变化曲线
plt.figure(figsize=(5,3))
plt.plot(ce,c='b',label="Loss")
plt.plot(acc,c='r',label="acc")
plt.legend()
plt.show()

输出结果为：
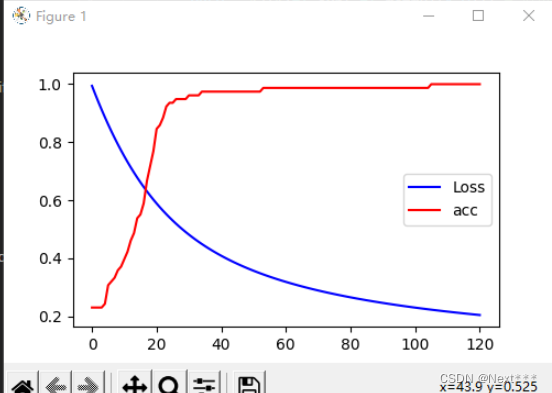
在这里插入图片描述

损失一直单调下降，所以损失下降曲线很光滑
而准确率上升到一定的数值之后，有时候会停留在某个时间一段时间，因此呈现出台阶上升的趋势

11.4.1.2.6.2 绘制决策边界
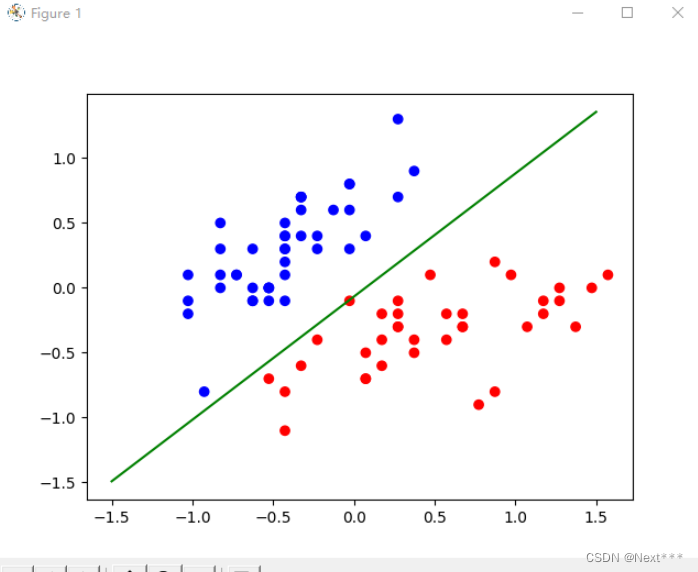
在这里插入图片描述

# 绘制决策边界
cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
x_ = [-1.5,1.5]
y_ = -(W[1]*x_+W[0])/W[2]
plt.plot(x_,y_,c='g')
plt.show()

输出结果为：
在这里插入图片描述
11.4.1.2.6.3 在训练过程中绘制决策边界

# 1 加载数据
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)

df_iris = pd.read_csv(train_path,header=0) # 是一个pandas二维数据表

# 2 处理数据
# 首先将二维数据表转化为numpy数组
iris= np.array(df_iris)  # shape(120,5)

# 提取属性和标签
train_x = iris[:,0:2]  # （120，2）
train_y = iris[:,4] # （120，）

# 提取山鸢尾和变色鸢尾，提取出标签纸为0和1的值
x_train = train_x[train_y < 2] # (78,2)
y_train = train_y[train_y < 2] # (78,)

# 记录现在的样本数
num = len(x_train)
# 中心化处理
x_train = x_train - np.mean(x_train,axis= 0)

# 生成多元模型的属性矩阵和标签列向量
x0_train = np.ones(num).reshape(-1,1)
X = tf.cast(tf.concat((x0_train,x_train),axis=1),tf.float32) # shape(78,3)
Y = tf.cast(y_train.reshape(-1,1),tf.float32) # shape(78,1)
# 可视化样本
#cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案
#plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
#plt.show()

# 3 设置超参数
learn_rate = 0.2 
iter = 120
display_step = 30

# 4 设置模型参数初始值
np.random.seed(612)
W = tf.Variable(np.random.randn(3,1),dtype=tf.float32)

cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案

x_ = [-1.5,1.5]
y_ = -(W[0]+W[1]*x_)/W[2]

plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
plt.plot(x_,y_,c='r',linewidth=3)
plt.xlim([-1.5,1.5])
plt.ylim([-1.5,1.5])

# 5 训练模型
ce = []
acc = []

for i in range(0,iter+1):
    with tf.GradientTape() as tape:
        PRED = 1/(1+tf.exp(-tf.matmul(X,W))) # 每个样本的预测概率
        Loss = -tf.reduce_mean(Y*tf.math.log(PRED)+(1-Y)*tf.math.log(1-PRED))

    accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED.numpy()<0.5,0.,1.),Y),tf.float32))
    ce.append(Loss)
    acc.append(accuracy)

    dL_dW = tape.gradient(Loss,W)
    W.assign_sub(learn_rate*dL_dW)

    if i % display_step ==0:
        print("i: %i, Acc: %f, Loss: %f" % (i,accuracy,Loss))
        y_ = -(W[0]+W[1]*x_)/W[2]
        plt.plot(x_,y_)

plt.show()

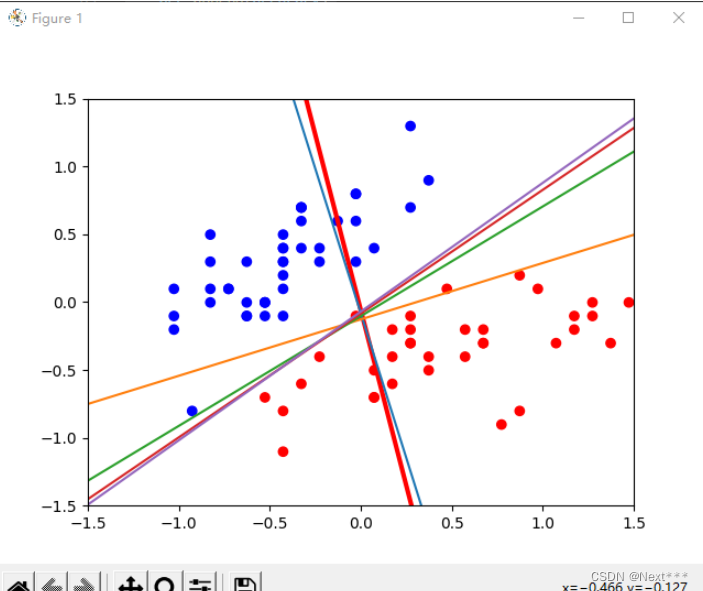
在这里插入图片描述

红色的是初始的，之后慢慢调增

11.4.1.2.7 使用测试集

# 1 加载数据
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
TEST_URL = "http://download.tensorflow.org/data/iris_test.csv"
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)
test_path = tf.keras.utils.get_file(TEST_URL.split('/')[-1],TEST_URL)

df_iris_train = pd.read_csv(train_path,header=0) # 是一个pandas二维数据表
df_iris_test =  pd.read_csv(test_path,header=0)

# 2 处理数据
# 首先将二维数据表转化为numpy数组
iris_train= np.array(df_iris_train)  # shape(120,5)
iris_test= np.array(df_iris_test)  # shape(30,5)

# 提取属性和标签
train_x = iris_train[:,0:2]  # （120，2）
train_y = iris_train[:,4] # （120，）

test_x = iris_test[:,0:2]  # （30，2）
test_y = iris_test[:,4] # （30，）
# 提取山鸢尾和变色鸢尾，提取出标签纸为0和1的值
x_train = train_x[train_y < 2] # (78,2)
y_train = train_y[train_y < 2] # (78,)

x_test = test_x[test_y < 2] # (22,2)
y_test = test_y[test_y < 2] # (22,)
# 记录现在的样本数
num_train = len(x_train)
num_test = len(x_test)
# 分别进行按列中心化处理，要求训练集和测试集独立同分布的，具有相同的均值和方差，数量有限的情况下，只要尽量接近即可
# 使用划分好的不用太考虑，但是自己划分数据集，要考虑这点
x_train = x_train - np.mean(x_train,axis= 0)
x_test = x_test - np.mean(x_test,axis=0)

# 生成多元模型的属性矩阵和标签列向量
x0_train = np.ones(num_train).reshape(-1,1)
X_train = tf.cast(tf.concat((x0_train,x_train),axis=1),tf.float32) # shape(78,3)
Y_train = tf.cast(y_train.reshape(-1,1),tf.float32) # shape(78,1)

x0_test = np.ones(num_test).reshape(-1,1)
X_test = tf.cast(tf.concat((x0_test,x_test),axis=1),dtype=tf.float32) # (22,3)
Y_test = tf.cast(y_test.reshape(-1,1),dtype=tf.float32) # (22,1)

# 可视化样本
#cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案
#plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
#plt.show()

# 3 设置超参数
learn_rate = 0.2 
iter = 120
display_step = 30

# 4 设置模型参数初始值
np.random.seed(612)
W = tf.Variable(np.random.randn(3,1),dtype=tf.float32)

cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案

x_ = [-1.5,1.5]
y_ = -(W[0]+W[1]*x_)/W[2]



# 5 训练模型
ce_train = []
acc_train = []
ce_test = []
acc_test = []

for i in range(0,iter+1):
    with tf.GradientTape() as tape:
        PRED_train = 1/(1+tf.exp(-tf.matmul(X_train,W))) # 每个样本的预测概率
        Loss_train = -tf.reduce_mean(Y_train*tf.math.log(PRED_train)+(1-Y_train)*tf.math.log(1-PRED_train))
        PRED_test = 1/(1+tf.exp(-tf.matmul(X_test,W))) # 每个样本的预测概率
        Loss_test = -tf.reduce_mean(Y_test*tf.math.log(PRED_test)+(1-Y_test)*tf.math.log(1-PRED_test))

    accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED_train.numpy()<0.5,0.,1.),Y_train),tf.float32))
    accuracy_test = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED_test.numpy()<0.5,0.,1.),Y_test),tf.float32))

    ce_train.append(Loss_train)
    acc_train.append(accuracy_train)
    ce_test.append(Loss_test)
    acc_test.append(accuracy_test)

    dL_dW = tape.gradient(Loss_train,W)
    W.assign_sub(learn_rate*dL_dW)

    if i % display_step ==0:
        print("i: %i, TrainAcc: %f, TrainLoss: %f, TestAcc: %f, TestLoss: %f" % (i,accuracy_train,Loss_train,accuracy_test,Loss_test))

# 6 可视化
plt.figure(figsize=(10,3))

plt.subplot(121)
plt.plot(ce_train,c='b',label="train")
plt.plot(ce_test,c='r',label="test")
plt.ylabel("Loss")
plt.legend()

plt.subplot(122)
plt.plot(acc_train,c='b',label="train")
plt.plot(acc_test,c='r',label="test")
plt.ylabel("Accuracy")

plt.legend()
plt.show()

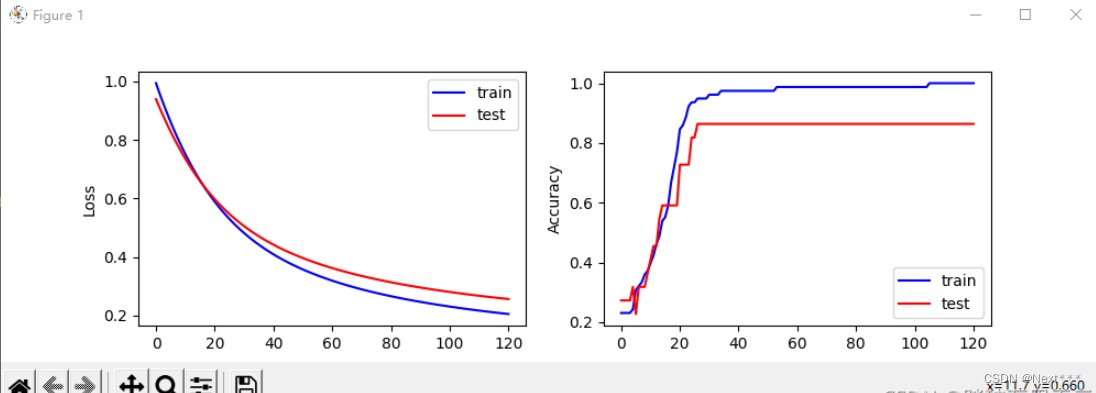
输出结果为：

i: 0, TrainAcc: 0.230769, TrainLoss: 0.994269, TestAcc: 0.272727, TestLoss: 0.939684
i: 30, TrainAcc: 0.961538, TrainLoss: 0.481892, TestAcc: 0.863636, TestLoss: 0.505456
i: 60, TrainAcc: 0.987179, TrainLoss: 0.319128, TestAcc: 0.863636, TestLoss: 0.362112
i: 90, TrainAcc: 0.987179, TrainLoss: 0.246626, TestAcc: 0.863636, TestLoss: 0.295611
i: 120, TrainAcc: 1.000000, TrainLoss: 0.204982, TestAcc: 0.863636, TestLoss: 0.256212

在这里插入图片描述

11.4.2 绘制分类图

在这里插入图片描述

11.4.2.1 生成网格坐标矩阵np.meshgrid()

X,Y = np.meshgrid(x,y)

11.4.2.2 填充网格 plt.pcolomesh()

11.4.2.2.1 rainbow色彩方案

plt.pcolomesh(X,Y,Z,cmap)

前两个参数：X和Y确定网格位置
第三个参数：Z决定网格的颜色
第四个参数：cmap指定所使用的颜色方案
可以使用plt.contourf()函数代替plt.pcolomesh()函数

# 1 加载数据
import tensorflow as tf
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

n = 10
x = np.linspace(-10,10,n)
y = np.linspace(-10,10,n)
X,Y = np.meshgrid(x,y)
Z = X+Y
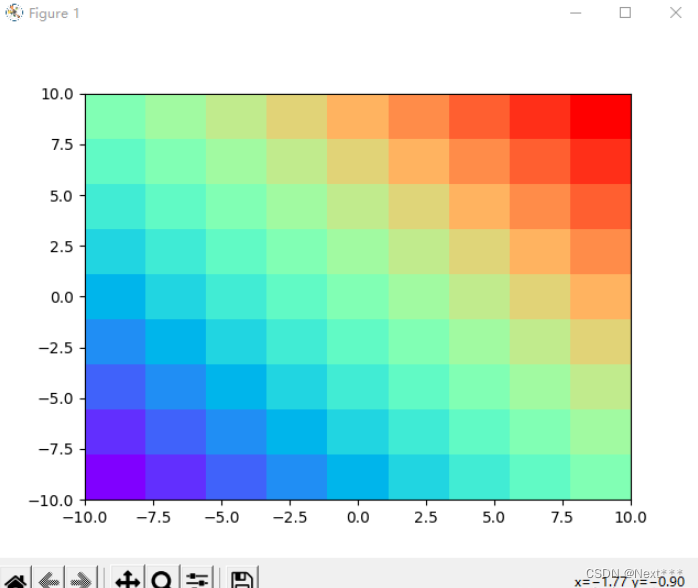
plt.pcolormesh(X,Y,Z,cmap="rainbow")

plt.show()

输出结果为：
在这里插入图片描述
11.4.2.2.2 自己定义的色彩方案

如果定义了两种颜色，就平均按照颜色值划分两类，如果是三种颜色，就划分为三个区域

# 1 加载数据
import tensorflow as tf
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

n = 200
x = np.linspace(-10,10,n)
y = np.linspace(-10,10,n)
X,Y = np.meshgrid(x,y)
Z = X+Y
cm_bg = mpl.colors.ListedColormap(["#FFA0A0","#A0FFA0"])
plt.pcolormesh(X,Y,Z,cmap=cm_bg)

plt.show()

输出结果为：
在这里插入图片描述

11.4.2.3 绘制轮廓线plt.contour()

plt.contour()：根据类的取值绘制出相同取值的边界
可以理解为三维模型的等高线

# 1 加载数据
import tensorflow as tf
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

n = 200
x = np.linspace(-10,10,n)
y = np.linspace(-10,10,n)
X,Y = np.meshgrid(x,y)
Z = X+Y

plt.contour(X,Y,Z,cmap="rainbow")

plt.show()

输出结果为：
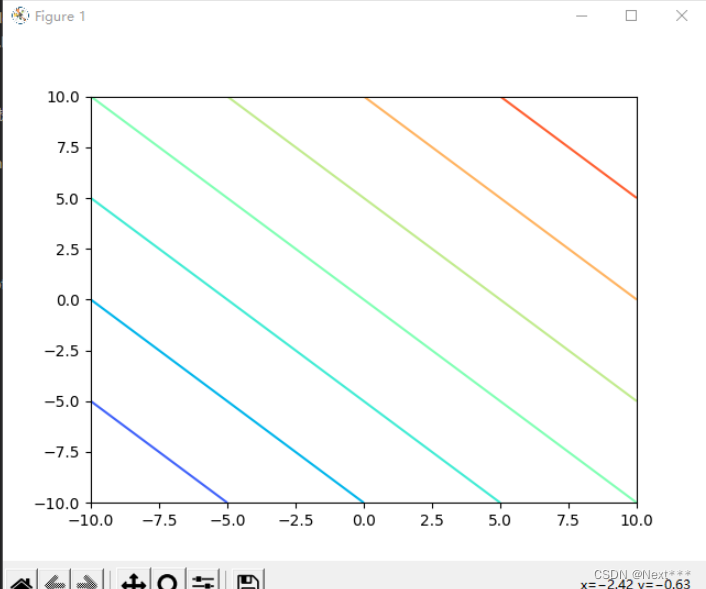
在这里插入图片描述
修改为

Z = X**2+Y**2

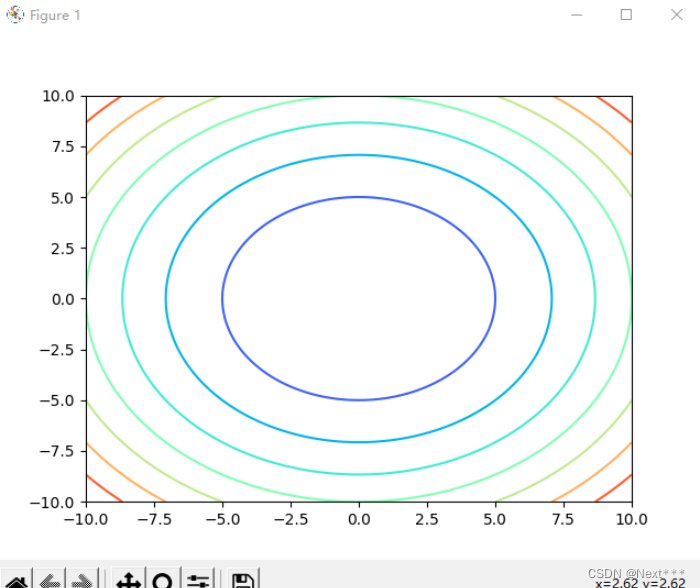
在这里插入图片描述
11.4.2.3.1 给轮廓线之间填充颜色plt.contourf(X,Y,Z,a,cmap)

填充分区

plt.contourf(X,Y,Z,a,cmap)

前两个参数：X和Y确定网格位置
第三个参数：Z决定网格的颜色
第四个参数：a，指定颜色细分的数量
第五个参数：cmap指定所使用的颜色方案
可以使用plt.contourf()函数代替plt.pcolomesh()函数

# 1 加载数据
import tensorflow as tf
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

n = 200
x = np.linspace(-10,10,n)
y = np.linspace(-10,10,n)
X,Y = np.meshgrid(x,y)
Z = X**2+Y**2

plt.contourf(X,Y,Z,cmap="rainbow")

plt.show()

输出结果为：
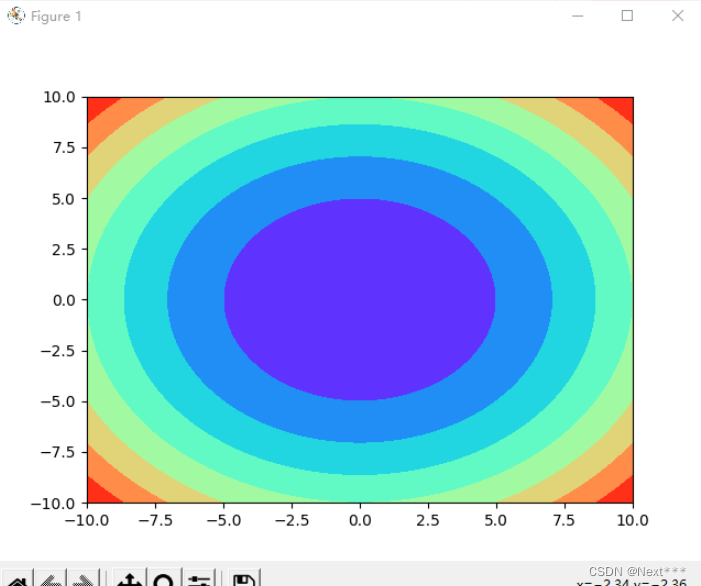
在这里插入图片描述

11.4.2.4 绘制分类图例子

# 1 加载数据
import tensorflow as tf
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

n = 200
x = np.linspace(-10,10,n)
y = np.linspace(-10,10,n)
X,Y = np.meshgrid(x,y)
Z = X+Y

cm_bg = mpl.colors.ListedColormap(["#FFA0A0","#A0FFA0"])
Z = tf.where(Z<5,0,1)
plt.contourf(X,Y,Z,cmap=cm_bg)

plt.show()

输出结果为：
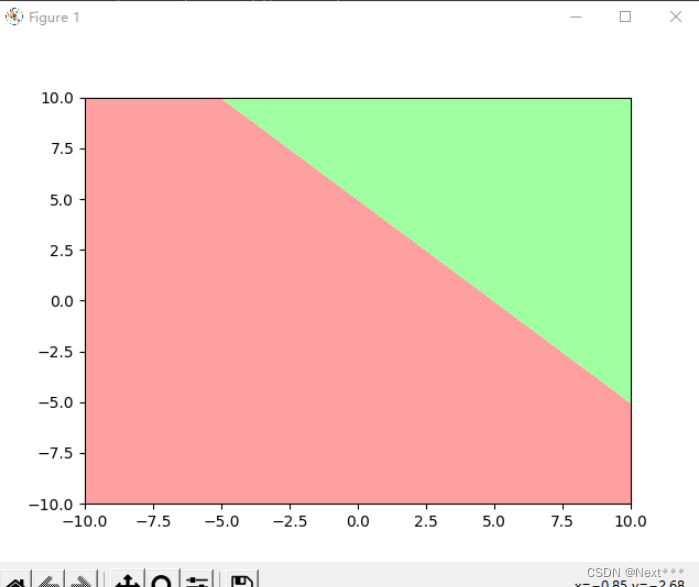
在这里插入图片描述

11.4.2.5 根据鸢尾花分类模型，绘制训练集和测试集分类图

# 1 加载数据
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
TEST_URL = "http://download.tensorflow.org/data/iris_test.csv"
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)
test_path = tf.keras.utils.get_file(TEST_URL.split('/')[-1],TEST_URL)

df_iris_train = pd.read_csv(train_path,header=0) # 是一个pandas二维数据表
df_iris_test =  pd.read_csv(test_path,header=0)

# 2 处理数据
# 首先将二维数据表转化为numpy数组
iris_train= np.array(df_iris_train)  # shape(120,5)
iris_test= np.array(df_iris_test)  # shape(30,5)

# 提取属性和标签
train_x = iris_train[:,0:2]  # （120，2）
train_y = iris_train[:,4] # （120，）

test_x = iris_test[:,0:2]  # （30，2）
test_y = iris_test[:,4] # （30，）
# 提取山鸢尾和变色鸢尾，提取出标签纸为0和1的值
x_train = train_x[train_y < 2] # (78,2)
y_train = train_y[train_y < 2] # (78,)

x_test = test_x[test_y < 2] # (22,2)
y_test = test_y[test_y < 2] # (22,)
# 记录现在的样本数
num_train = len(x_train)
num_test = len(x_test)
# 分别进行按列中心化处理，要求训练集和测试集独立同分布的，具有相同的均值和方差，数量有限的情况下，只要尽量接近即可
# 使用划分好的不用太考虑，但是自己划分数据集，要考虑这点
x_train = x_train - np.mean(x_train,axis= 0)
x_test = x_test - np.mean(x_test,axis=0)

# 生成多元模型的属性矩阵和标签列向量
x0_train = np.ones(num_train).reshape(-1,1)
X_train = tf.cast(tf.concat((x0_train,x_train),axis=1),tf.float32) # shape(78,3)
Y_train = tf.cast(y_train.reshape(-1,1),tf.float32) # shape(78,1)

x0_test = np.ones(num_test).reshape(-1,1)
X_test = tf.cast(tf.concat((x0_test,x_test),axis=1),dtype=tf.float32) # (22,3)
Y_test = tf.cast(y_test.reshape(-1,1),dtype=tf.float32) # (22,1)

# 可视化样本
#cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案
#plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
#plt.show()

# 3 设置超参数
learn_rate = 0.2 
iter = 120
display_step = 30

# 4 设置模型参数初始值
np.random.seed(612)
W = tf.Variable(np.random.randn(3,1),dtype=tf.float32)

cm_pt = mpl.colors.ListedColormap(["blue","red"]) # 设置色彩方案

x_ = [-1.5,1.5]
y_ = -(W[0]+W[1]*x_)/W[2]



# 5 训练模型
ce_train = []
acc_train = []
ce_test = []
acc_test = []

for i in range(0,iter+1):
    with tf.GradientTape() as tape:
        PRED_train = 1/(1+tf.exp(-tf.matmul(X_train,W))) # 每个样本的预测概率
        Loss_train = -tf.reduce_mean(Y_train*tf.math.log(PRED_train)+(1-Y_train)*tf.math.log(1-PRED_train))
        PRED_test = 1/(1+tf.exp(-tf.matmul(X_test,W))) # 每个样本的预测概率
        Loss_test = -tf.reduce_mean(Y_test*tf.math.log(PRED_test)+(1-Y_test)*tf.math.log(1-PRED_test))

    accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED_train.numpy()<0.5,0.,1.),Y_train),tf.float32))
    accuracy_test = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED_test.numpy()<0.5,0.,1.),Y_test),tf.float32))

    ce_train.append(Loss_train)
    acc_train.append(accuracy_train)
    ce_test.append(Loss_test)
    acc_test.append(accuracy_test)

    dL_dW = tape.gradient(Loss_train,W)
    W.assign_sub(learn_rate*dL_dW)

    if i % display_step ==0:
        print("i: %i, TrainAcc: %f, TrainLoss: %f, TestAcc: %f, TestLoss: %f" % (i,accuracy_train,Loss_train,accuracy_test,Loss_test))

# 6 可视化
# 根据鸢尾花分类模型，绘制分类图
# 定义绘制散点的颜色方案
cm_pt = mpl.colors.ListedColormap(["blue","red"])
# 定义背景颜色方案
cm_bg = mpl.colors.ListedColormap(["#FFA0A0","#A0FFA0"])
plt.rcParams['font.sans-serif']="SimHei"


plt.figure(figsize=(15,5))

# 绘制训练集
plt.subplot(121)
M = 300
x1_min,x2_min = x_train.min(axis=0)
x1_max,x2_max = x_train.max(axis=0)
t1 = np.linspace(x1_min,x1_max,M) # 使用花萼长度的取值范围作为横坐标取值范围
t2 = np.linspace(x2_min,x2_max,M) # 使用花萼宽度的取值范围作为纵坐标取值范围
m1,m2 = np.meshgrid(t1,t2) # 生成网格点坐标矩阵

m0 = np.ones(M*M)
# 生成多元线性模型需要的属性矩阵
X_mesh = tf.cast(np.stack((m0,m1.reshape(-1),m2.reshape(-1)),axis=1),dtype=tf.float32)
# 使用训练得到的W，根据sigmoid公式计算所有网格点对应的函数值
Y_mesh = tf.cast(1/(1+tf.exp(-tf.matmul(X_mesh,W))),dtype=tf.float32)
# 把分类结果转化为0，1，作为填充粉色，还是绿色的依据
Y_mesh = tf.where(Y_mesh<0.5,0,1)

# 并对其进行唯独变换，使其和m1，m2有相同的形状
n = tf.reshape(Y_mesh,m1.shape)

# 注意，TensorFlow中的绘图是有层次的，首先绘制分区图作为背景，然后在上面绘制散点图
# 绘制分区图
plt.pcolormesh(m1,m2,n,cmap=cm_bg)
# 绘制散点图
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
plt.title("训练集分类图",fontsize = 14)
plt.legend()

# 绘制测试集
plt.subplot(122)
M = 300
x1_min,x2_min = x_test.min(axis=0)
x1_max,x2_max = x_test.max(axis=0)
t1 = np.linspace(x1_min,x1_max,M) # 使用花萼长度的取值范围作为横坐标取值范围
t2 = np.linspace(x2_min,x2_max,M) # 使用花萼宽度的取值范围作为纵坐标取值范围
m1,m2 = np.meshgrid(t1,t2) # 生成网格点坐标矩阵

m0 = np.ones(M*M)
# 生成多元线性模型需要的属性矩阵
X_mesh = tf.cast(np.stack((m0,m1.reshape(-1),m2.reshape(-1)),axis=1),dtype=tf.float32)
# 使用训练得到的W，根据sigmoid公式计算所有网格点对应的函数值
Y_mesh = tf.cast(1/(1+tf.exp(-tf.matmul(X_mesh,W))),dtype=tf.float32)
# 把分类结果转化为0，1，作为填充粉色，还是绿色的依据
Y_mesh = tf.where(Y_mesh<0.5,0,1)

# 并对其进行唯独变换，使其和m1，m2有相同的形状
n = tf.reshape(Y_mesh,m1.shape)

# 注意，TensorFlow中的绘图是有层次的，首先绘制分区图作为背景，然后在上面绘制散点图
# 绘制分区图
plt.pcolormesh(m1,m2,n,cmap=cm_bg)
# 绘制散点图
plt.scatter(x_test[:,0],x_test[:,1],c=y_test,cmap=cm_pt)
plt.title("测试集分类图",fontsize = 14)
plt.legend()

plt.show()
x1_max,x2_max = x_train.max(axis=0)
t1 = np.linspace(x1_min,x1_max,M) # 使用花萼长度的取值范围作为横坐标取值范围
t2 = np.linspace(x2_min,x2_max,M) # 使用花萼宽度的取值范围作为纵坐标取值范围
m1,m2 = np.me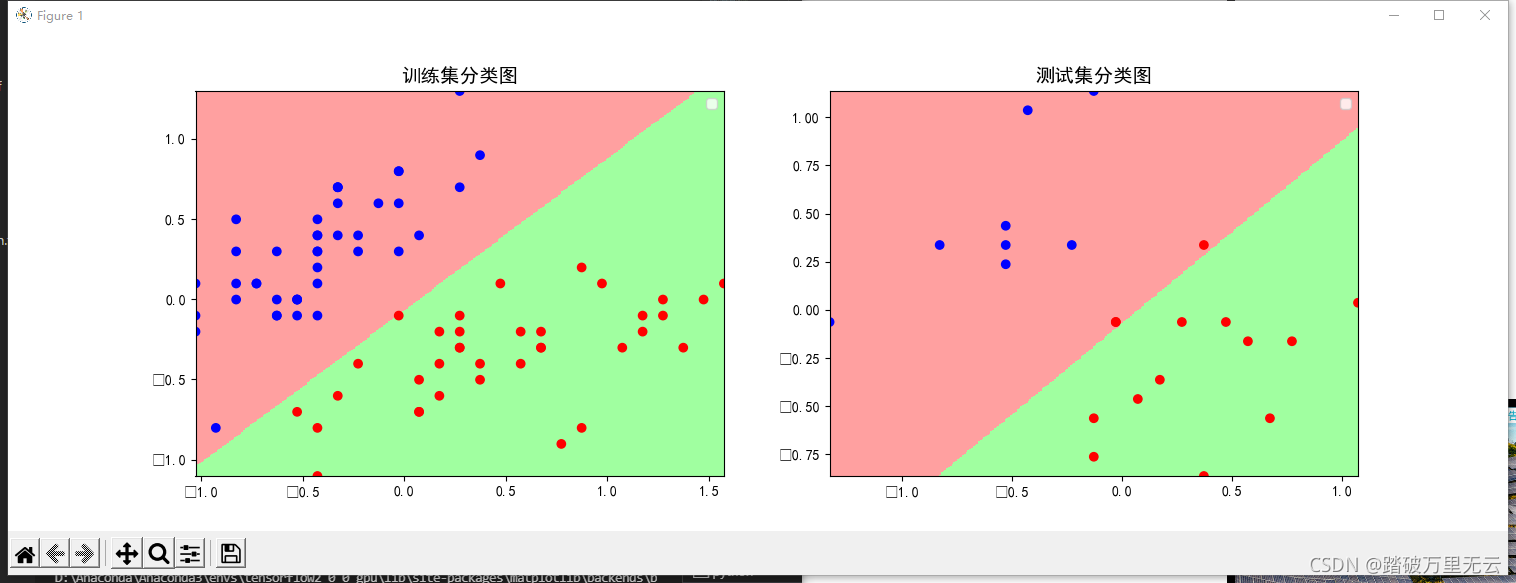![请添加图片描述](https://img-blog.csdnimg.cn/d10de77e0af24661b01b7c524b707407.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA6LiP56C05LiH6YeM5peg5LqR,size_20,color_FFFFFF,t_70,g_se,x_16)
shgrid(t1,t2) # 生成网格点坐标矩阵

m0 = np.ones(M*M)
# 生成多元线性模型需要的属性矩阵
X_mesh = tf.cast(np.stack((m0,m1.reshape(-1),m2.reshape(-1)),axis=1),dtype=tf.float32)
# 使用训练得到的W，根据sigmoid公式计算所有网格点对应的函数值
Y_mesh = tf.cast(1/(1+tf.exp(-tf.matmul(X_mesh,W))),dtype=tf.float32)
# 把分类结果转化为0，1，作为填充粉色，还是绿色的依据
Y_mesh = tf.where(Y_mesh<0.5,0,1)

# 并对其进行唯独变换，使其和m1，m2有相同的形状
n = tf.reshape(Y_mesh,m1.shape)

# 注意，TensorFlow中的绘图是有层次的，首先绘制分区图作为背景，然后在上面绘制散点图
# 绘制分区图
plt.pcolormesh(m1,m2,n,cmap=cm_bg)
# 绘制散点图
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)


# 绘制测试集
plt.subplot(122)
M = 300
x1_min,x2_min = x_test.min(axis=0)
x1_max,x2_max = x_test.max(axis=0)
t1 = np.linspace(x1_min,x1_max,M) # 使用花萼长度的取值范围作为横坐标取值范围
t2 = np.linspace(x2_min,x2_max,M) # 使用花萼宽度的取值范围作为纵坐标取值范围
m1,m2 = np.meshgrid(t1,t2) # 生成网格点坐标矩阵

m0 = np.ones(M*M)
# 生成多元线性模型需要的属性矩阵
X_mesh = tf.cast(np.stack((m0,m1.reshape(-1),m2.reshape(-1)),axis=1),dtype=tf.float32)
# 使用训练得到的W，根据sigmoid公式计算所有网格点对应的函数值
Y_mesh = tf.cast(1/(1+tf.exp(-tf.matmul(X_mesh,W))),dtype=tf.float32)
# 把分类结果转化为0，1，作为填充粉色，还是绿色的依据
Y_mesh = tf.where(Y_mesh<0.5,0,1)

# 并对其进行唯独变换，使其和m1，m2有相同的形状
n = tf.reshape(Y_mesh,m1.shape)

# 注意，TensorFlow中的绘图是有层次的，首先绘制分区图作为背景，然后在上面绘制散点图
# 绘制分区图
plt.pcolormesh(m1,m2,n,cmap=cm_bg)
# 绘制散点图
plt.scatter(x_test[:,0],x_test[:,1],c=y_test,cmap=cm_pt)
plt.show()

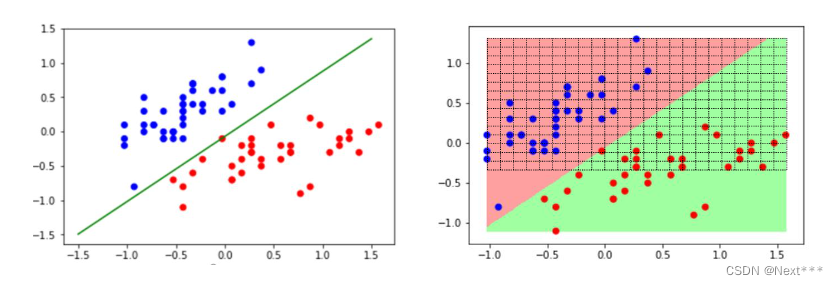
输出结果为：
在这里插入图片描述

测试集上看着有两个分类错误，其实是三个，因为测试集里面有两个重合点

11.4.2.5 使用定义函数借鉴上一节代码

讨论【11.4】绘制测试集分类图
课程编程实例中，有很多代码是重复的，是否可以通过函数来实现代码复用？同学们尝试一下，并在讨论区分享关键代码，大家共同学习。

#加载数据
import tensorflow as tf
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
from numpy.lib.function_base import disp

#数据准备
def preparedData(URL):
    path=tf.keras.utils.get_file(URL.split('/')[-1],URL)
    df_iris=pd.read_csv(path,header=0)
    iris=np.array(df_iris)
    _x=iris[:,0:2]
    _y=iris[:,4]
    x=_x[_y<2]
    y=_y[_y<2]
    num=len(x)
    X,Y,x=dataCentralize(x,y,num)
    return X,Y,x,y

#数据中心化
def dataCentralize(x,y,num):
    x=x-np.mean(x,axis=0)
    x0=np.ones(num).reshape(-1,1)
    X=tf.cast(tf.concat((x0,x),axis=1),tf.float32)
    Y=tf.cast(y.reshape(-1,1),tf.float32)
    return X,Y,x

#获取导数
def getDerivate(X,Y,W,ce,acc,flag):
    with tf.GradientTape() as tape:
        PRED=1/(1+tf.exp(-tf.matmul(X,W)))
        Loss=-tf.reduce_mean(Y*tf.math.log(PRED)+(1-Y)*tf.math.log(1-PRED))
        accuracy=tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED.numpy()<0.5,0.,1.),Y),tf.float32))
        ce.append(Loss)

        acc.append(accuracy)
        if  flag==1:
            dL_dW=tape.gradient(Loss,W)
            W.assign_sub(learn_rate*dL_dW)
    return ce,acc,W

#绘图
def mapping(x,y):
    M=300
    x1_min,x2_min=x.min(axis=0)
    x1_max,x2_max=x.max(axis=0)
    t1=np.linspace(x1_min,x1_max,M)
    t2=np.linspace(x2_min,x2_max,M)
    m1,m2=np.meshgrid(t1,t2)
    m0=np.ones(M*M)
    X_mesh=tf.cast(np.stack((m0,m1.reshape(-1),m2.reshape(-1)),axis=1),dtype=tf.float32)
    Y_mesh=tf.cast(1/(1+tf.exp(-tf.matmul(X_mesh,W))),dtype=tf.float32)
    Y_mesh=tf.where(Y_mesh<0.5,0,1)
    n=tf.reshape(Y_mesh,m1.shape)
    cm_pt=mpl.colors.ListedColormap(["blue","red"])
    cm_bg=mpl.colors.ListedColormap(["#FFA0A0","#A0FFA0"])
    plt.pcolormesh(m1,m2,n,cmap=cm_bg)
    plt.scatter(x[:,0],x[:,1],c=y,cmap=cm_pt)
    plt.show()

#数据加载
TRAIN_URL="https://download.tensorflow.org/data/iris_training.csv"
TEST_URL="https://download.tensorflow.org/data/iris_test.csv"
X_train,Y_train,x_train,y_train=preparedData(TRAIN_URL)
X_test,Y_test,x_test,y_test=preparedData(TEST_URL)

#设置超参
learn_rate=0.2
iter=120
display_step=30

#设置模型参数初始值
np.random.seed(612)
W=tf.Variable(np.random.randn(3,1),dtype=tf.float32)

#训练模型
ce_train=[]
acc_train=[]
ce_test=[]
acc_test=[]

for i in range(0,iter+1):
    acc_train,ce_train,W=getDerivate(X_train,Y_train,W,ce_train,acc_train,1)
    acc_test,ce_test,W=getDerivate(X_train,Y_train,W,ce_train,acc_train,1)
    if i % display_step==0:
        print("i:%i\tAcc:%f\tLoss:%f\tAcc_test:%f\tLoss_test:%f"%(i,acc_train[i],ce_train[i],acc_test[i],ce_test[i]))

#绘图#x_train,y_train,
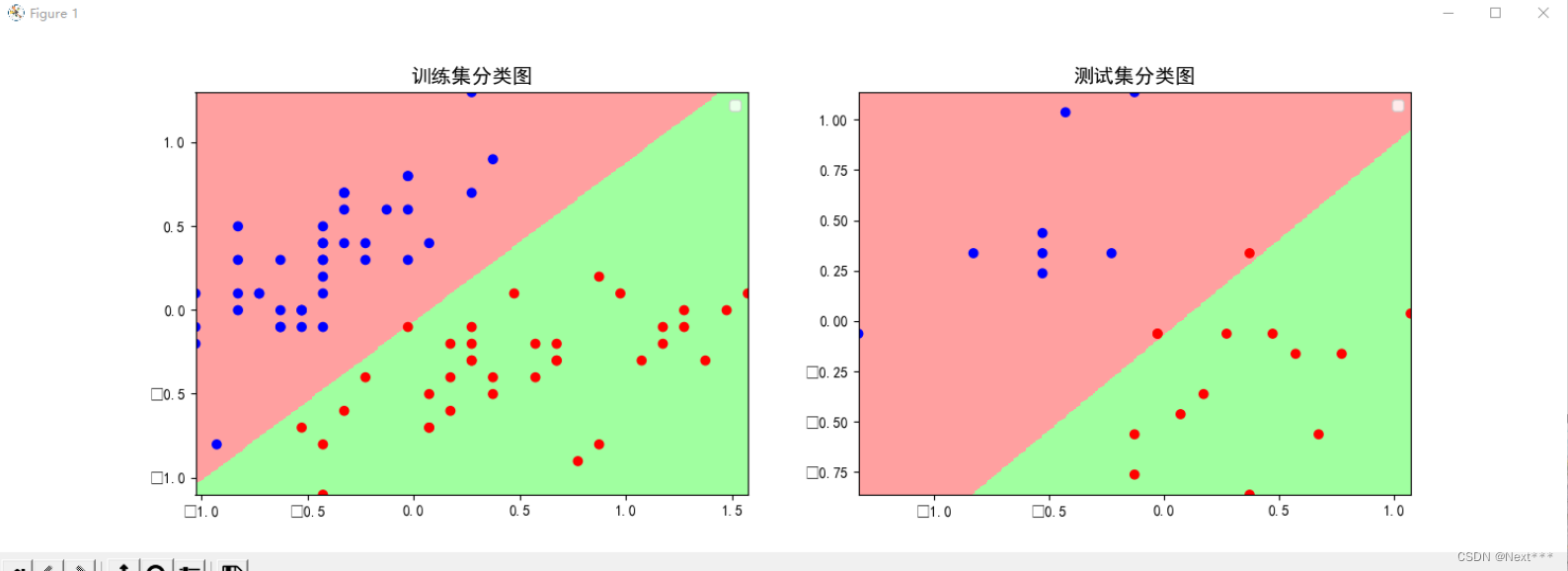
mapping(x_test,y_test)

输出结果为：

i:0     Acc:0.994269    Loss:0.230769   Acc_test:0.230769       Loss_test:0.994269
i:30    Acc:0.961538    Loss:0.481892   Acc_test:0.481892       Loss_test:0.961538
i:60    Acc:0.319128    Loss:0.987179   Acc_test:0.987179       Loss_test:0.319128
i:90    Acc:0.987179    Loss:0.246626   Acc_test:0.246626       Loss_test:0.987179
i:120   Acc:0.204982    Loss:1.000000   Acc_test:1.000000       Loss_test:0.204982

在这里插入图片描述

11.4.2.6 使用四种属性区分变色鸢尾和维吉尼亚鸢尾

鸢尾花数据集中，有四个属性（花瓣长度、花瓣宽度、花萼长度、花萼宽度），课程中只是给出了两种属性组合的情况，如果采用三种或者四种属性去训练模型，能否把变色鸢尾和维吉尼亚鸢尾完全区分开呢？请简要说明一下你用的哪几种属性并在讨论区晒出你的程序结果。

# 1 加载数据
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
TEST_URL = "http://download.tensorflow.org/data/iris_test.csv"
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)
test_path = tf.keras.utils.get_file(TEST_URL.split('/')[-1],TEST_URL)

df_iris_train = pd.read_csv(train_path,header=0) # 是一个pandas二维数据表
df_iris_test =  pd.read_csv(test_path,header=0)

# 2 处理数据
# 首先将二维数据表转化为numpy数组
iris_train= np.array(df_iris_train)  # shape(120,5)
iris_test= np.array(df_iris_test)  # shape(30,5)

# 提取属性和标签
train_x = iris_train[:,0:4]  # （120，4）
train_y = iris_train[:,4] # （120，）

test_x = iris_test[:,0:4]  # （30，4）
test_y = iris_test[:,4] # （30，）
# 提取山鸢尾和变色鸢尾，提取出标签纸为0和1的值
x_train = train_x[train_y > 0] # (n,4)
y_train = train_y[train_y > 0]-1 # (n,)

x_test = test_x[test_y > 0] # (m,4)
y_test = test_y[test_y > 0]-1 # (m,)
# 记录现在的样本数
num_train = len(x_train)
num_test = len(x_test)
# 分别进行按列中心化处理，要求训练集和测试集独立同分布的，具有相同的均值和方差，数量有限的情况下，只要尽量接近即可
# 使用划分好的不用太考虑，但是自己划分数据集，要考虑这点

x_train = x_train - np.mean(x_train,axis= 0)
x_test = x_test - np.mean(x_test,axis=0)

# 生成多元模型的属性矩阵和标签列向量
x0_train = np.ones(num_train).reshape(-1,1)
X_train = tf.cast(tf.concat((x0_train,x_train),axis=1),tf.float32) # shape(n,5)
Y_train = tf.cast(y_train.reshape(-1,1),tf.float32) # shape(n,1)

x0_test = np.ones(num_test).reshape(-1,1)
X_test = tf.cast(tf.concat((x0_test,x_test),axis=1),dtype=tf.float32) # (m,5)
Y_test = tf.cast(y_test.reshape(-1,1),dtype=tf.float32) # (m,1)

# 3 设置超参数
learn_rate = 0.135
iter = 10000
display_step = 1000

# 4 设置模型参数初始值
np.random.seed(612)
W = tf.Variable(np.random.randn(5,1),dtype=tf.float32)

# 5 训练模型
ce_train = []
acc_train = []
ce_test = []
acc_test = []

for i in range(0,iter+1):
    with tf.GradientTape() as tape:
        PRED_train = 1/(1+tf.exp(-tf.matmul(X_train,W))) # 每个样本的预测概率
        Loss_train = -tf.reduce_mean(Y_train*tf.math.log(PRED_train)+(1-Y_train)*tf.math.log(1-PRED_train))
        PRED_test = 1/(1+tf.exp(-tf.matmul(X_test,W))) # 每个样本的预测概率
        Loss_test = -tf.reduce_mean(Y_test*tf.math.log(PRED_test)+(1-Y_test)*tf.math.log(1-PRED_test))

    accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED_train.numpy()<0.5,0.,1.),Y_train),tf.float32))
    accuracy_test = tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED_test.numpy()<0.5,0.,1.),Y_test),tf.float32))

    ce_train.append(Loss_train)
    acc_train.append(accuracy_train)
    ce_test.append(Loss_test)
    acc_test.append(accuracy_test)

    dL_dW = tape.gradient(Loss_train,W)
    W.assign_sub(learn_rate*dL_dW)

    if i % display_step ==0:
        print("i: %i, TrainAcc: %f, TrainLoss: %f, TestAcc: %f, TestLoss: %f" % (i,accuracy_train,Loss_train,accuracy_test,Loss_test))

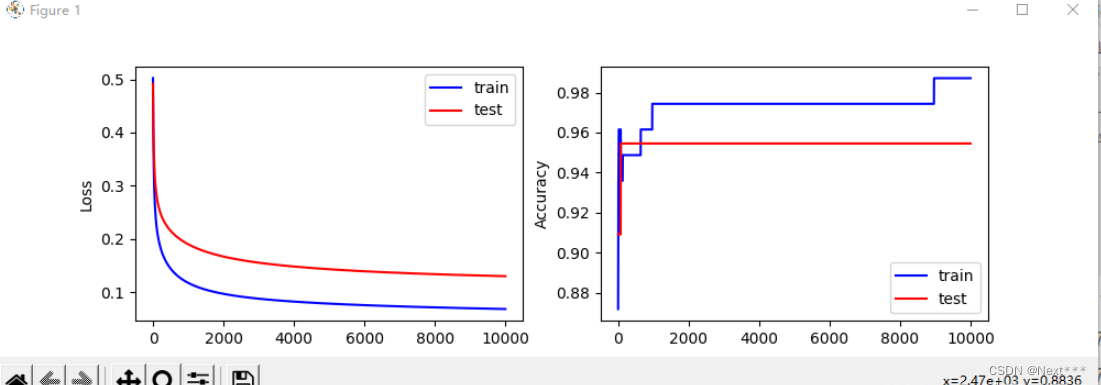
#可视化：绘制损失和准确率变化曲线
plt.figure(figsize=(10,3))
plt.subplot(121)
plt.plot(ce_train,color="blue",label="train")
plt.plot(ce_test,color="red",label="test")
plt.ylabel("Loss")
plt.legend()

plt.subplot(122)
plt.plot(acc_train,color="blue",label="train")
plt.plot(acc_test,color="red",label="test")
plt.ylabel("Accuracy")
plt.legend()

plt.show()

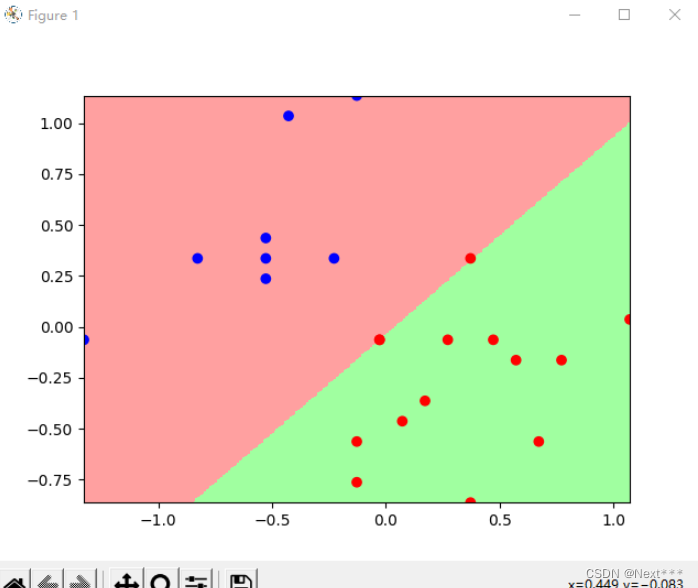
输出结果为：

i: 0, TrainAcc: 0.871795, TrainLoss: 0.502093, TestAcc: 0.909091, TestLoss: 0.491409
i: 1000, TrainAcc: 0.974359, TrainLoss: 0.117291, TestAcc: 0.954545, TestLoss: 0.189897
i: 2000, TrainAcc: 0.974359, TrainLoss: 0.096742, TestAcc: 0.954545, TestLoss: 0.166818
i: 3000, TrainAcc: 0.974359, TrainLoss: 0.087580, TestAcc: 0.954545, TestLoss: 0.155260
i: 4000, TrainAcc: 0.974359, TrainLoss: 0.082096, TestAcc: 0.954545, TestLoss: 0.148034
i: 5000, TrainAcc: 0.974359, TrainLoss: 0.078296, TestAcc: 0.954545, TestLoss: 0.142953
i: 6000, TrainAcc: 0.974359, TrainLoss: 0.075425, TestAcc: 0.954545, TestLoss: 0.139118
i: 7000, TrainAcc: 0.974359, TrainLoss: 0.073129, TestAcc: 0.954545, TestLoss: 0.136092
i: 8000, TrainAcc: 0.974359, TrainLoss: 0.071221, TestAcc: 0.954545, TestLoss: 0.133636
i: 9000, TrainAcc: 0.987179, TrainLoss: 0.069592, TestAcc: 0.954545, TestLoss: 0.131605
i: 10000, TrainAcc: 0.987179, TrainLoss: 0.068172, TestAcc: 0.954545, TestLoss: 0.129906

在这里插入图片描述

11.5 多分类问题

逻辑回归：二分类问题
多分类问题：把输入样本划分为多个类别
下面以鸢尾花为例，实现多分类类别

11.5.1 类别编码问题

自然顺序码
0 —— 山鸢尾（Setosa）
1 —— 变色鸢尾（Versicolour）
2 —— 维吉尼亚鸢尾（Virginica）
欧氏距离使得类别之间不平等，但是实际上类别之间应该是平等的
独热编码（One-Hot Encoding）
使非偏序关系的数据，取值不具有偏序性
到原点等距
（1，0，0） —— 山鸢尾（Setosa）
（0，1，0） —— 变色鸢尾（Versicolour）
（0，0，1） —— 维吉尼亚鸢尾（Virginica）
需要占用更多的空间，但是能够更加合理的表示数据之间的关系，可以有效的避免学习中的偏差
独热的应用
离散的特征
多分类问题中的类别标签
独冷编码（One-Hot Encoding）
（0，1，1） —— 山鸢尾（Setosa）
（1，0，1） —— 变色鸢尾（Versicolour）
（1，1，0） —— 维吉尼亚鸢尾（Virginica）

11.5.2 实例，多分类问题

例：使用属性花瓣长度和花瓣宽度，构造分类器，能够识别3种类型的鸢尾花

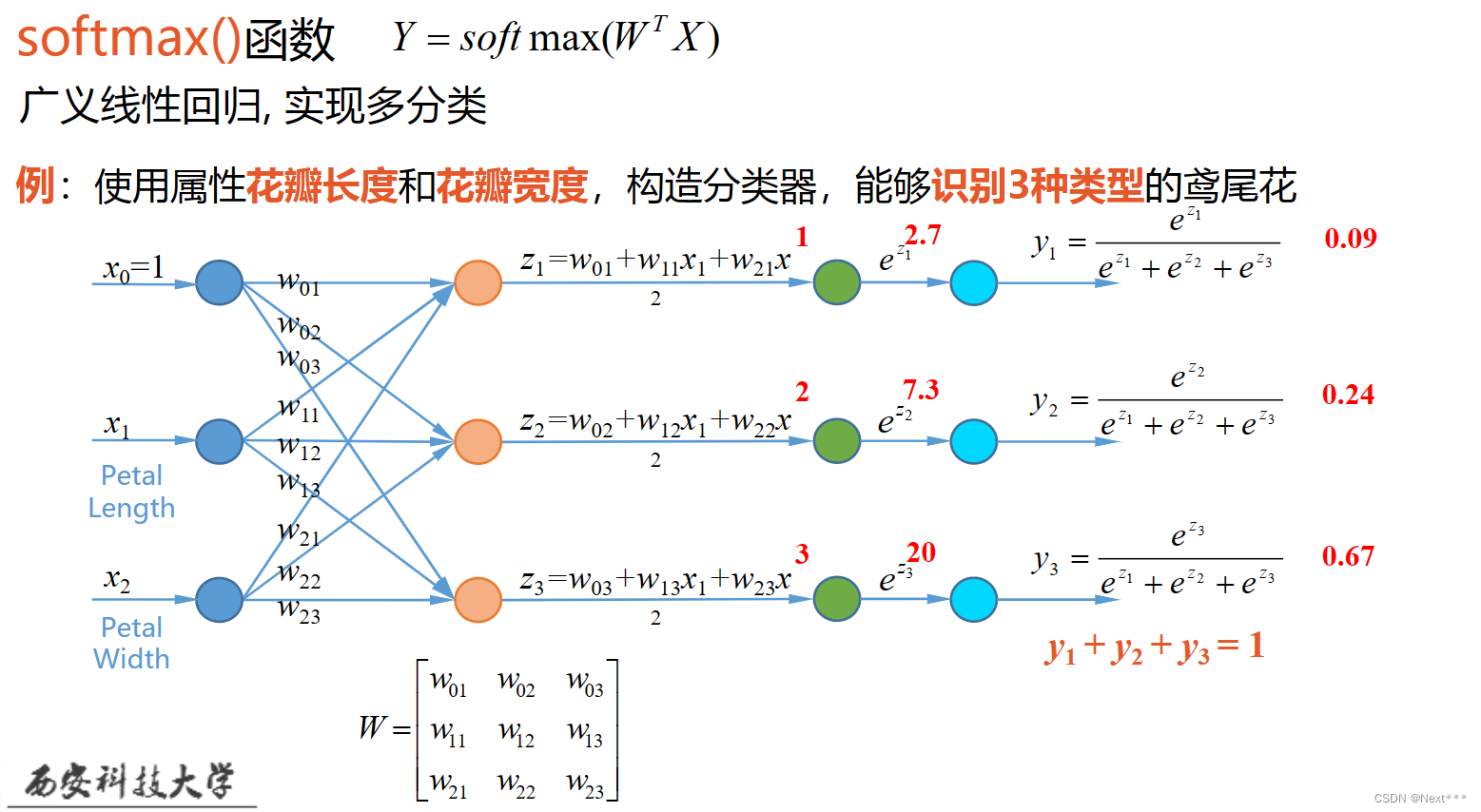
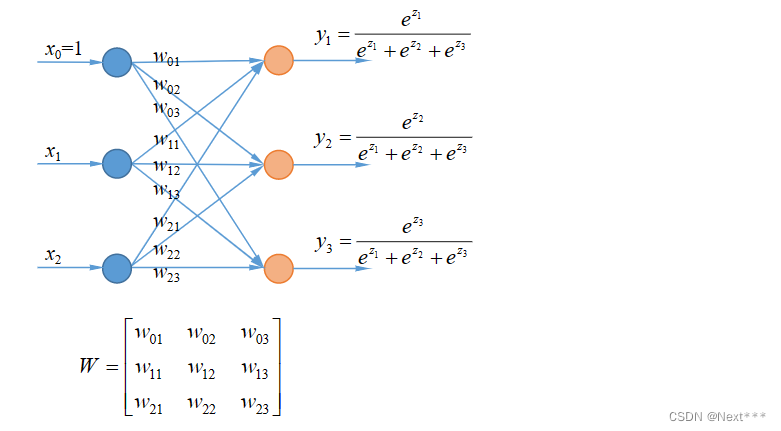
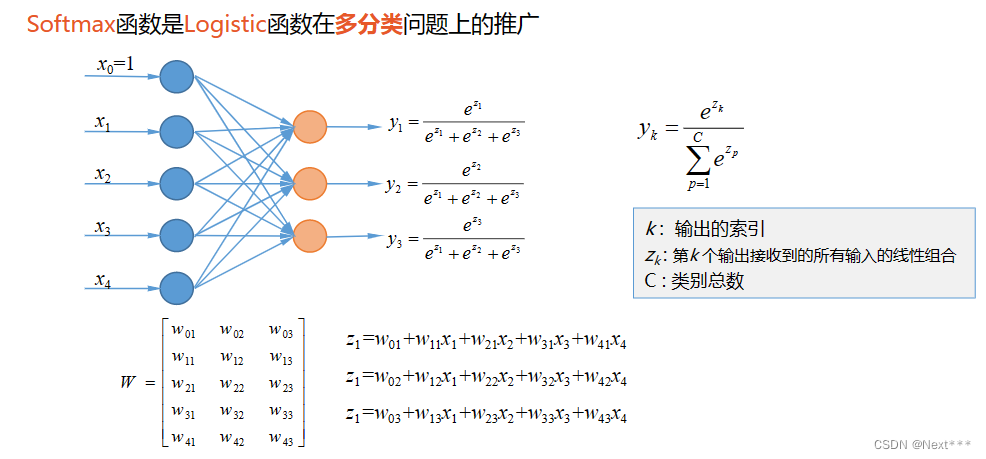
在这里插入图片描述

互斥的多分类问题：每个样本只能够属于一个类别
鸢尾花的识别
手写数字的识别
标签：一个图片可以被打上多个标签，即一个样本可以同时属于多个类别
彩色图片
包括人物的图片
包括汽车的图片
户外图片
室内图片

11.6 实例：多分类问题

11.6.1 独热编码的实现

tf.one_hot(indices,depth)

indices：一维数组/张量
depth：编码深度，也就是分成几类

>>> import tensorflow as tf
>>> print(tf.__version__)   
2.0.0
>>> import numpy as np
>>> a = [0,2,3,5]
>>> b = tf.one_hot(a,6)
>>> b
<tf.Tensor: id=9, shape=(4, 6), dtype=float32, numpy=
array([[1., 0., 0., 0., 0., 0.],
       [0., 0., 1., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0.],
       [0., 0., 0., 0., 0., 1.]], dtype=float32)>

11.6.2 准确率的计算

# 预测值
>>> pred = np.array([[0.1,0.2,0.7],[0.1,0.7,0.2],[0.3,0.4,0.3]]) 
# 标记
>>> y = np.array([2,1,0]) 
# 标记独热编码
>>> y_onehot = np.array([[0,0,1],[0,1,0],[1,0,0]]) 
# 预测值中的最大数索引
>>> tf.argmax(pred,axis=1) 
<tf.Tensor: id=12, shape=(3,), dtype=int64, numpy=array([2, 1, 1], dtype=int64)>
# 判读预测值是否与样本标记相同
>>> tf.equal(tf.argmax(pred,axis=1),y) 
<tf.Tensor: id=17, shape=(3,), dtype=bool, numpy=array([ True,  True, False])>
# 将布尔值转化为数字
>>> tf.cast(tf.equal(tf.argmax(pred,axis=1),y),tf.float32) 
<tf.Tensor: id=23, shape=(3,), dtype=float32, numpy=array([1., 1., 0.], dtype=float32)>
# 计算准确率
>>> tf.reduce_mean(tf.cast(tf.equal(tf.argmax(pred,axis=1),y),tf.float32))
<tf.Tensor: id=39, shape=(), dtype=float32, numpy=0.6666667>

11.6.3 交叉熵损失函数的实现

代码接11.6.2

>>> -y_onehot*tf.math.log(pred) 
<tf.Tensor: id=43, shape=(3, 3), dtype=float64, numpy=
array([[-0.        , -0.        ,  0.35667494],       
       [-0.        ,  0.35667494, -0.        ],       
       [ 1.2039728 , -0.        , -0.        ]])>     
# 所有样本交叉熵之和
>>> -tf.reduce_sum(y_onehot*tf.math.log(pred)) 
<tf.Tensor: id=50, shape=(), dtype=float64, numpy=1.917322692203401>
# 平均交叉熵损失
>>> -tf.reduce_sum(y_onehot*tf.math.log(pred))/len(pred) 
<tf.Tensor: id=59, shape=(), dtype=float64, numpy=0.6391075640678003>
>>> len(pred) 
3

11.6.4 使用花瓣长度、花瓣宽度将三种鸢尾花区分开

11.6.4.0 修改动态分配显存(空)

11.6.4.1 加载数据

# 1 加载数据
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# 修改配置-动态分配显存
gpus = tf.config.experimental.list_physical_devices(device_type='GPU')
tf.config.experimental.set_memory_growth(gpus[0], True)

TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
TEST_URL = "http://download.tensorflow.org/data/iris_test.csv"

train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)
test_path = tf.keras.utils.get_file(TEST_URL.split('/')[-1],TEST_URL)

df_iris_train = pd.read_csv(train_path, header=0)

11.6.4.2 处理数据

# 2 处理数据
iris_train = np.array(df_iris_train)
# (120,5)

#提取花瓣长度、花瓣宽度属性 
x_train = iris_train[:,2:4]
# (120,2)
y_train = iris_train[:,4]
# (120,)

num_train = len(x_train)

x0_train = np.ones(num_train).reshape(-1,1)
X_train = tf.cast(tf.concat([x0_train,x_train],axis=1),tf.float32)
# ([120,3])
Y_train = tf.one_hot(tf.constant(y_train,dtype=tf.int32),3)
# ([120,3])

11.6.4.3 设置超参数、设置模型参数初始值

# 3 设置超参数、设置模型参数初始值
learn_rate = 0.2
iter = 500
display_step = 100

np.random.seed(612)
W = tf.Variable(np.random.randn(3,3),dtype=tf.float32)

11.6.4.4 训练模型

# 4 训练模型
acc = []
cce = []

for i in range(0,iter+1):
    with tf.GradientTape() as tape:
        # (120,3) 属于每种类别的概率，每个样本三种类别概率之和为1
        PRED_train = tf.nn.softmax(tf.matmul(X_train,W))
        Loss_train = -tf.reduce_sum(Y_train*tf.math.log(PRED_train))/num_train

    accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(PRED_train.numpy(),axis=1),y_train),tf.float32))

    acc.append(accuracy)
    cce.append(Loss_train)

    dL_dW = tape.gradient(Loss_train,W)
    W.assign_sub(learn_rate*dL_dW)

    if i % display_step == 0:
        print("i: %i, Acc: %f, Loss: %f"%(i,accuracy,Loss_train))

输出结果为：

i: 0, Acc: 0.350000, Loss: 4.510763
i: 100, Acc: 0.808333, Loss: 0.503537
i: 200, Acc: 0.883333, Loss: 0.402912
i: 300, Acc: 0.891667, Loss: 0.352650
i: 400, Acc: 0.941667, Loss: 0.319778
i: 500, Acc: 0.941667, Loss: 0.295599

11.6.4.5 查看训练结果

# 5 查看训练结果
# 输出自然顺序码
print("自然顺序码为：" )
print(tf.argmax(PRED_train.numpy(),axis=1))
``
输出结果为：

```python
自然顺序码为：
tf.Tensor(
[2 1 2 0 0 0 0 2 1 0 1 1 0 0 2 2 2 2 2 0 2 2 0 1 1 0 1 2 1 2 1 1 1 2 2 2 2
 2 0 0 2 2 2 0 0 1 0 2 0 2 0 1 1 0 1 2 2 2 2 1 1 2 2 2 1 2 0 2 2 0 0 1 0 2
 2 0 1 1 1 2 0 1 1 1 2 0 1 1 2 0 2 1 0 0 2 0 0 2 2 0 0 1 0 1 0 0 0 0 1 0 2
 1 0 2 0 1 1 0 0 1], shape=(120,), dtype=int64)

11.6.4.6 绘制分类图


# 6 绘制分类图
M = 500
x1_min,x2_min = x_train.min(axis=0)
x1_max,x2_max = x_train.max(axis=0)
t1 = np.linspace(x1_min,x1_max,M)
t2 = np.linspace(x2_min,x2_max,M)
m1,m2 = np.meshgrid(t1,t2)

m0 = np.ones(M*M)
X_ = tf.cast(np.stack((m0,m1.reshape(-1),m2.reshape(-1)),axis=1),tf.float32)
Y_ = tf.nn.softmax(tf.matmul(X_,W))

Y_ = tf.argmax(Y_.numpy(),axis=1)# 转换为自然顺序码

n = tf.reshape(Y_,m1.shape)# (500,500)

plt.figure(figsize = (8,6))
cm_bg =  mpl.colors.ListedColormap(['#A0FFA0','#FFA0A0','#A0A0FF'])

plt.pcolormesh(m1,m2,n,cmap=cm_bg)
plt.scatter(x_train[:,0],x_train[:,1],c = y_train,cmap="brg")

plt.show()

11.6.4.7 本例代码汇总

# 1 加载数据
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

gpus = tf.config.experimental.list_physical_devices(device_type='GPU')
tf.config.experimental.set_memory_growth(gpus[0], True)

TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
TEST_URL = "http://download.tensorflow.org/data/iris_test.csv"

train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)
test_path = tf.keras.utils.get_file(TEST_URL.split('/')[-1],TEST_URL)

df_iris_train = pd.read_csv(train_path, header=0)

# 2 处理数据
iris_train = np.array(df_iris_train)
# (120,5)

#提取花瓣长度、花瓣宽度属性 
x_train = iris_train[:,2:4]
# (120,2)
y_train = iris_train[:,4]
# (120,)

num_train = len(x_train)

x0_train = np.ones(num_train).reshape(-1,1)
X_train = tf.cast(tf.concat([x0_train,x_train],axis=1),tf.float32)
# ([120,3])
Y_train = tf.one_hot(tf.constant(y_train,dtype=tf.int32),3)
# ([120,3])

# 3 设置超参数、设置模型参数初始值
learn_rate = 0.2
iter = 500
display_step = 100

np.random.seed(612)
W = tf.Variable(np.random.randn(3,3),dtype=tf.float32)

# 4 训练模型
acc = []
cce = []

for i in range(0,iter+1):
    with tf.GradientTape() as tape:
        
        PRED_train = tf.nn.softmax(tf.matmul(X_train,W))
        # (120,3) 属于每种类别的概率，每个样本三种类别概率之和为1
        Loss_train = -tf.reduce_sum(Y_train*tf.math.log(PRED_train))/num_train

    accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(PRED_train.numpy(),axis=1),y_train),tf.float32))

    acc.append(accuracy)
    cce.append(Loss_train)

    dL_dW = tape.gradient(Loss_train,W)
    W.assign_sub(learn_rate*dL_dW)

    if i % display_step == 0:
        print("i: %i, Acc: %f, Loss: %f"%(i,accuracy,Loss_train))

# 5 查看训练结果
# 输出自然顺序码
print("自然顺序码为：" )
print(tf.argmax(PRED_train.numpy(),axis=1))

# 6 绘制分类图
M = 500
x1_min,x2_min = x_train.min(axis=0)
x1_max,x2_max = x_train.max(axis=0)
t1 = np.linspace(x1_min,x1_max,M)
t2 = np.linspace(x2_min,x2_max,M)
m1,m2 = np.meshgrid(t1,t2)

m0 = np.ones(M*M)
X_ = tf.cast(np.stack((m0,m1.reshape(-1),m2.reshape(-1)),axis=1),tf.float32)
Y_ = tf.nn.softmax(tf.matmul(X_,W))

Y_ = tf.argmax(Y_.numpy(),axis=1)# 转换为自然顺序码

n = tf.reshape(Y_,m1.shape)# (500,500)

plt.figure(figsize = (8,6))
cm_bg =  mpl.colors.ListedColormap(['#A0FFA0','#FFA0A0','#A0A0FF'])

plt.pcolormesh(m1,m2,n,cmap=cm_bg)
plt.scatter(x_train[:,0],x_train[:,1],c = y_train,cmap="brg")

plt.show()