写在前面
本篇文章开始学习数据结构的图的相关知识,涉及的基本概念还是很多的。
本文的行文思路:
学习图的基本概念
学习图的存储结构——本文主要介绍邻接矩阵和邻接表
对每种结构进行深度优先遍历和广度优先遍历
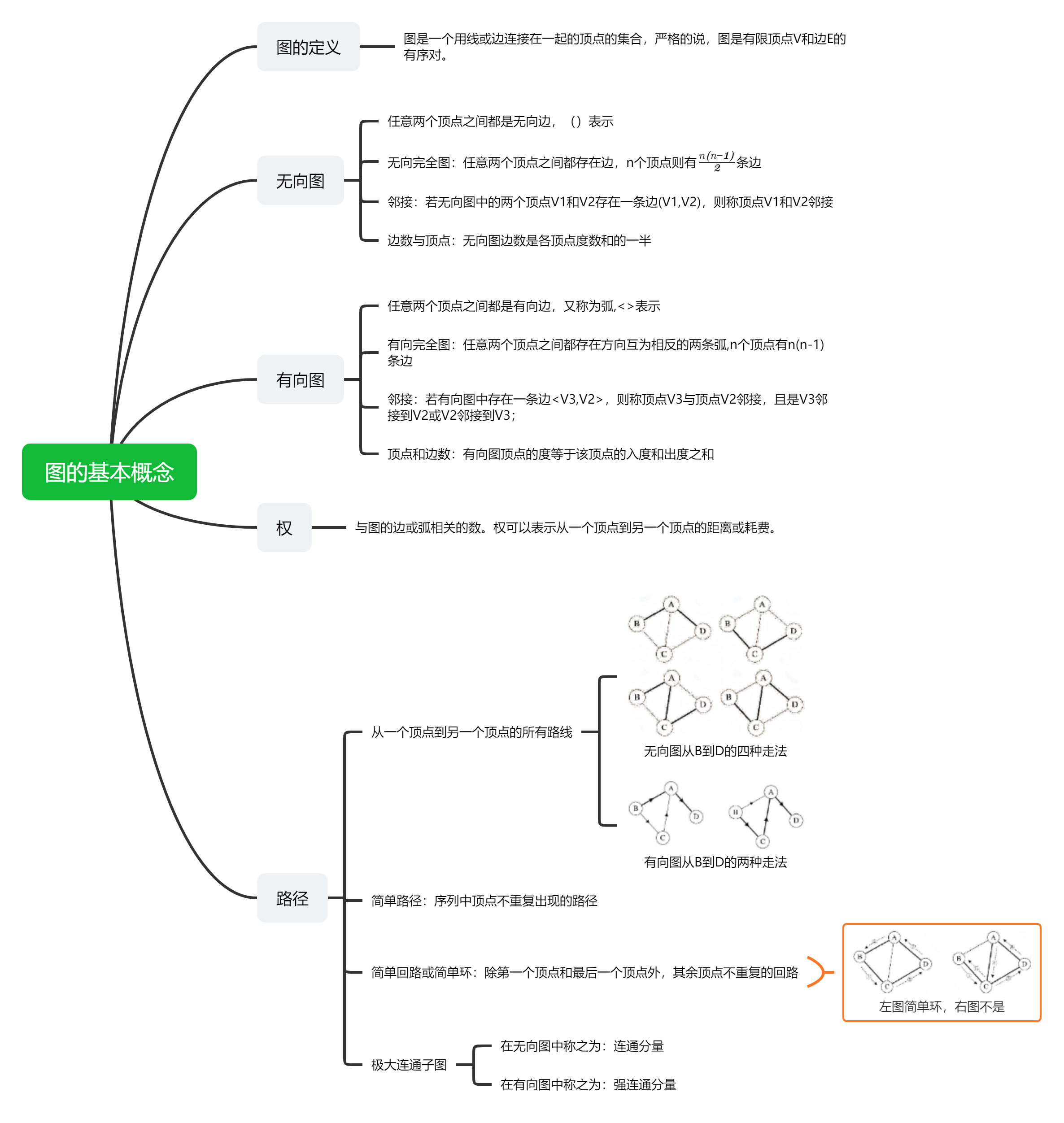
先识概念
话不多说,狠活献上
学习思想
等等,先别急,正式学习之前先认识几个英语单词及缩写
类型(Type)
顶点(vertex)
边(Edge)
邻接(adjacency,简写adj)
邻接矩阵(adjacency Matrix)
邻接表(adjacency List)
深度优先遍历(Depth First Search,简称BFS)
广度优先遍历(Breadth First Search,简称DFS)
邻接矩阵的存储结构
typedef char VertexType; //顶点类型
typedef int EdgeType; //边类型
#define MAXVEX 100 //最大顶点数目
#define INFINITY 65535 //用65535表示无穷
//邻接矩阵的存储结构
typedef struct
{
VertexType vexs[MAXVEX]; //顶点数组
EdgeType arc[MAXVEX][MAXVEX]; //边数组
int numVertexes, numEdges; //当前顶点的顶点数和边数
}MGraph;邻接表的存储结构
#define MAXVEX 100
typedef char VertexType; //顶点类型
typedef int EdgeType; //边上的权值类型
int visited[MAXVEX];
typedef struct EdgeNode //边表结点
{
int adjvex; //存储该顶点对应的下标
EdgeType info; //存储权值,非网图则无需
struct EdgeNode* next;
}EdgeNode;
typedef struct VertexNode //顶点结点
{
VertexType data; //存储顶点信息
EdgeNode* firstedge; //边表头指针
}VertexNode, AdjList[MAXVEX];
//邻接表存储结构
typedef struct
{
AdjList adjList;
int numVertexes, numEdges; //当前顶点数目和边数
}GraphAdjList;再学应用
邻接矩阵的深度遍历和广度遍历
深度遍历:实际上就是二叉树的前序遍历
广度遍历:实际上就是二叉树的层序遍历,要用到队列,我们自己还要写出队列的一些基本操作
#include<stdio.h>
#include<malloc.h>
typedef char VertexType; //顶点类型
typedef int EdgeType; //边类型
#define MAXVEX 100 //最大顶点数目
#define INFINITY 65535 //用65535表示无穷
//邻接矩阵的存储结构
typedef struct
{
VertexType vexs[MAXVEX]; //顶点数组
EdgeType arc[MAXVEX][MAXVEX]; //边数组
int numVertexes, numEdges; //当前顶点的顶点数和边数
}MGraph;
//邻接矩阵的初始化
void CreateMGraph(MGraph* G)
{
int i, j, k;
printf("请输入顶点的个数和边数:");
scanf("%d%d", &G->numVertexes, &G->numEdges);
for (i = 0; i < G->numVertexes; i++)
{
printf("请输入%d个顶点: ", i + 1);
scanf("%s", &G->vexs[i]);
}
//将矩阵的所有数据初始化为"无穷"
for (i = 0; i < G->numVertexes; i++)
for (j = 0; j < G->numVertexes; j++)
G->arc[i][j] = INFINITY;
//然后自定义矩阵中的数据
for (k = 0; k < G->numEdges; k++)
{
printf("请输入边(vi,vj)中的下标i和j: ");
scanf("%d%d", &i, &j);
G->arc[i][j] = 1;
G->arc[j][i] = G->arc[i][j]; //无向图的邻接矩阵沿着右对角线对称
}
}
int visited[MAXVEX]; //访问标志的数组
//深度优先递归算法
void DFS(MGraph G, int i)
{
int j;
visited[i] = 1; //将第i个顶点标记为已访问
printf("%c ", G.vexs[i]); //打印顶点,也可以是其他操作
//循环遍历G中所有的顶点
for (j = 0; j < G.numVertexes; j++)
{
//判断当前正在遍历的顶点j和顶点i是否相邻且未被访问过,相连为1,不相连为0(前提是不带权的图)
if (G.arc[i][j] == 1 && !visited[j])
DFS(G, j);
}
}
//邻接矩阵的深度遍历操作
void DFSTraverse(MGraph G)
{
int i;
//初始化所有顶点状态都是未访问过的
for (i = 0; i < G.numVertexes; i++)
{
visited[i] = 0;
}
//对所有未访问过的顶点调用DFS,若为连通图则只执行一次
for (i = 0; i < G.numVertexes; i++)
{
if (!visited[i])
DFS(G, i);
}
}
//队列的顺序存储结构
typedef struct
{
char data[MAXVEX];
int front;
int rear;
}SqQueue;
void InitQueue(SqQueue* Q)
{
Q->front = 0;
Q->rear = 0;
}
void EnQueue(SqQueue* Q,int e)
{
if ((Q->rear + 1) % MAXVEX == Q->front)
return;
Q->data[Q->rear] = e;
Q->rear = (Q->rear + 1) % MAXVEX;
}
void DeQueue(SqQueue* Q, int* e)
{
if (Q->front == Q->rear)
return;
*e = Q->data[Q->front];
Q->front = (Q->front + 1) % MAXVEX;
}
int QueueEmpty(SqQueue Q)
{
return Q.front == Q.rear;
}
//邻接矩阵的广度遍历
void BFSTraverse(MGraph G)
{
int i, j;
SqQueue Q;
for (i = 0; i < G.numVertexes; i++)
{
visited[i] = 0; //将每一个顶点都设置未访问
}
InitQueue(&Q); //初始化一个辅助用的队列
for (i = 0; i < G.numVertexes; i++)
{
if (!visited[i])
{
visited[i] = 1; //设置当前顶点为已访问
printf("%c ", G.vexs[i]);
EnQueue(&Q, i); //将此顶点入队列
while (!QueueEmpty(Q))
{
DeQueue(&Q, &i); //首元素出队,赋给i
for (j = 0; j < G.numVertexes; j++)
{
if (G.arc[i][j] == 1 && !visited[j]) //边存在且未被访问过
{
visited[j] = 1; //设置当前顶点为已访问
printf("%c ", G.vexs[j]); //打印顶点
EnQueue(&Q, j); //将此顶点入队
}
}
}
}
}
}
int main()
{
MGraph G;
CreateMGraph(&G);
printf("DFS遍历顺序:");
DFSTraverse(G);
printf("\n");
printf("BFS遍历顺序:");
BFSTraverse(G);
printf("\n");
return 0;
}
邻接表的深度遍历和广度遍历
#define _CRT_SECURE_NO_WARNINGS 1
//图的遍历主要有两种,深度优先遍历和广度优先遍历
//深度优先遍历实际上是二叉树的先序遍历,广度优先遍历实际上是二叉树的层序遍历
#include<stdio.h>
#include<malloc.h>
#define MAXVEX 100
typedef char VertexType; //顶点类型
typedef int EdgeType; //边上的权值类型
int visited[MAXVEX];
typedef struct EdgeNode //边表结点
{
int adjvex; //存储该顶点对应的下标
EdgeType info; //存储权值,非网图则无需
struct EdgeNode* next;
}EdgeNode;
typedef struct VertexNode //顶点结点
{
VertexType data; //存储顶点信息
EdgeNode* firstedge; //边表头指针
}VertexNode, AdjList[MAXVEX];
//邻接表存储结构
typedef struct
{
AdjList adjList;
int numVertexes, numEdges; //当前顶点数目和边数
}GraphAdjList;
//邻接表的初始化
void CreateALGraph(GraphAdjList* GL)
{
int i, j, k;
EdgeNode* e;
printf("输入顶点数和边数:");
scanf("%d%d", &GL->numVertexes, &GL->numEdges);
//将数据存进顶点数组,把顶点指针域置空
for (i = 0; i < GL->numVertexes; i++)
{
getchar();
printf("请输入第%d个顶点:", i + 1);
scanf("%c", &GL->adjList[i].data);
GL->adjList[i].firstedge = NULL;
}
for (k = 0; k < GL->numEdges; k++)
{
printf("输入边(vi,vj)上的顶点序号:");
scanf("%d%d", &i, &j);
//结点i记录结点j的下标
e = (EdgeNode*)malloc(sizeof(EdgeNode));
e->adjvex = j;
e->next = GL->adjList[i].firstedge; //下面两步相当于链表的头插法
GL->adjList[i].firstedge = e;
//结点j记录结点i的下标
e = (EdgeNode*)malloc(sizeof(EdgeNode));
e->adjvex = i;
e->next = GL->adjList[j].firstedge; //下面两步相当于链表的头插法
GL->adjList[j].firstedge = e;
}
}
//邻接表的深度优先递归算法
void DFS(GraphAdjList GL, int i)
{
EdgeNode* p;
visited[i] = 1;
printf("%c ", GL.adjList[i].data);
p = GL.adjList[i].firstedge;
while (p)
{
if (!visited[p->adjvex])
DFS(GL, p->adjvex);
p = p->next;
}
}
//邻接表的深度遍历操作
void DFSTraverse(GraphAdjList GL)
{
int i;
for (i = 0; i < GL.numVertexes; i++)
{
visited[i] = 0;
}
for (i = 0; i < GL.numVertexes; i++)
{
if (!visited[i])
DFS(GL, i);
}
}
//队列的顺序存储结构
typedef struct
{
char data[MAXVEX];
int front;
int rear;
}SqQueue;
void InitQueue(SqQueue* Q)
{
Q->front = 0;
Q->rear = 0;
}
void EnQueue(SqQueue* Q, int e)
{
if ((Q->rear + 1) % MAXVEX == Q->front)
return;
Q->data[Q->rear] = e;
Q->rear = (Q->rear + 1) % MAXVEX;
}
void DeQueue(SqQueue* Q, int* e)
{
if (Q->front == Q->rear)
return;
*e = Q->data[Q->front];
Q->front = (Q->front + 1) % MAXVEX;
}
int QueueEmpty(SqQueue Q)
{
return Q.front == Q.rear;
}
//邻接表的广度优先遍历
void BFSTraverse(GraphAdjList GL)
{
int i;
EdgeNode* p;
SqQueue Q;
Q.front = Q.rear = 0;
for (i = 0; i < GL.numVertexes; i++)
{
visited[i] = 0;
if (!visited[i])
{
visited[i] = 1;
printf("%c ", GL.adjList[i].data);
EnQueue(&Q, i);
while (!QueueEmpty(Q))
{
DeQueue(&Q, &i);
p = GL.adjList[i].firstedge;
while (p)
{
if (!visited[p->adjvex])
{
visited[p->adjvex] = 1;
printf("%c ", GL.adjList[p->adjvex].data);
EnQueue(&Q, p->adjvex);
}
p = p->next;
}
}
}
}
}
int main()
{
GraphAdjList GL;
CreateALGraph(&GL);
printf("DFS遍历顺序:");
DFSTraverse(GL);
printf("\n");
printf("BFS遍历顺序:");
BFSTraverse(GL);
printf("\n");
return 0;
}一点补充
下面补充一个小知识点,就是typedef定义数组类型,先看下面的代码是什么意思呢?
typedef struct VertexNode AdjList[MAXVEX];
上面语句的意思是:定义一个元素类型是 struct VertexNode,含有MAXVEX个元素的数组类型
换个例子:
typedef int vector[10];
vector v1,v2;
语句定义了vector类型的两个对象v1和v2,每个对象都是vector类型的一个数组,每个数组由10个整型元素所组成。
写在最后
上面的代码难免会有疏漏,如果各位大佬发现错误,请一定要指正🙏
👍🏻 点赞,你的认可是我创作的动力!
⭐ 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富!