序言

笔记根据labuladong进行总结，极力推荐labuladong算法进行学习！！

树

0、算法一开始就应该刷树，了解递归的思想。
1、C语言中定义了一个结构体，然后申明一个指针指向这个结构体，那么我们要用指针取出结构体中的数据，就要用到“->”. 类成员用“.”，定义指针用*。

「结构」

//cpp
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
//注意学习new时带入初始值的写法

「遍历」

/* 二叉树遍历框架 */
void traverse(TreeNode root) {
    // 前序遍历
    traverse(root.left)
    // 中序遍历
    traverse(root.right)
    // 后序遍历
}

1、前后中序列遍历指的是父节点的位置
2、写递归算法的关键是要明确函数的「定义」是什么，然后相信这个定义，利用这个定义推导最终结果。以父root与子三个关节点进行考虑含义；先搞清楚

root是否为nullptr
当前 root 节点该做什么（函数体），获取孩子的值？还是其他，但对象都是root不是child
然后根据函数定义递归调用子节点，即孩子的null由下一级的递归判断！
考虑是前后中三种遍历中哪一种

「经验」

1、利用数组索引作为函数的参数，进行递归
2、数据输入，记得要构建树的结点：TreeNode root = new TreeNode(rootVal);
3、遍历就是找，返回void，访问就是改树，返回时treenode
4、return;指的是不再进行深入，可以等同于break;
5、链表和树是一样的思路；

「跨父节点」

做法就是增加函数参数，一个节点做不到，我们就给他安排两个节点，「将每一层二叉树节点连接起来」可以细化成「将每两个相邻节点都连接起来」,然后思考两个root 里面会进行什么操作；
对于增加参数的问题：一般从父子操作会转化为参数和root之间的操作，与孩子没有关系，孩子只是作为递归参数进入到下一轮；所以思考递归函数的参数更新的值怎么写！；
详细见是否为BST的错误代码和正确代码的区别
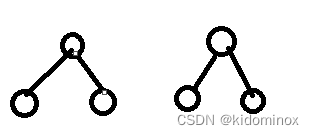
在这里插入图片描述