1、问题

2、思路（DP）

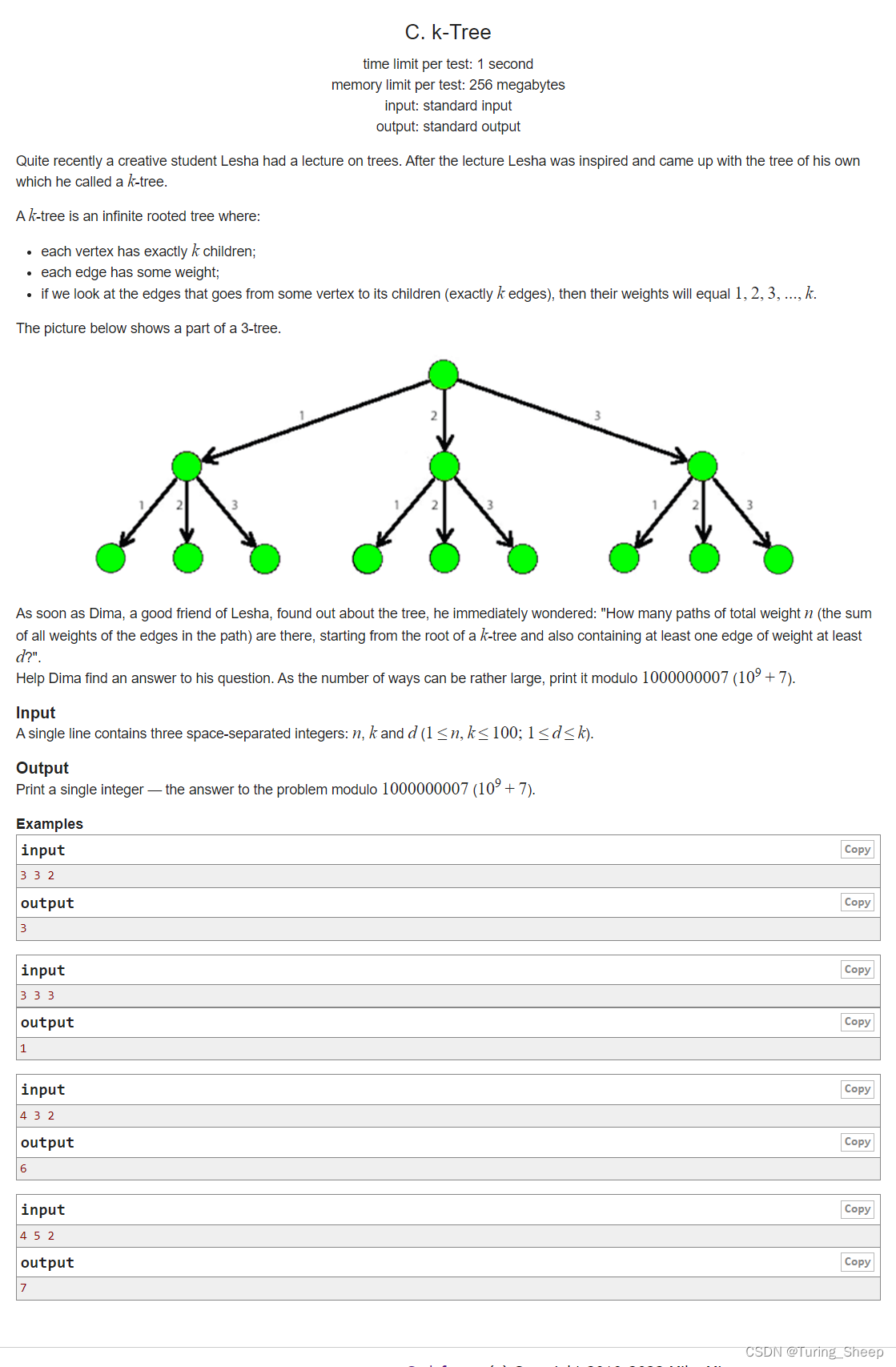
这道题翻译过来就是说，给我们一个k叉树，然后每个点到子节点的边的边权从左到右依次为1到k。然后我们从根节点出发，向下走，我们走过的边权之和记作$n$。

现在给我们一个n，我们需要找到满足边权和为n的路径条数。同时，题目还给了我们一个d，这个d的意思就是我们的路径中至少存在一条边是大于等于d的。

我们使用DP来解决这道题：
$f[n]$表示路径和为$n$的总条数，暂时先不管$d$。那么这个点可以由$1$到$k$表示出来。
$$f[i]=\sum _{j=1}^{k}f[i-j]$$

那么题目中的$d$的限制怎么体现呢？

我们可以求出不满足条件的情况，再用刚才的$f[n]$减去即可。
对于不满足条件的情况，我们记作$g[n]$
$$g[i]=\sum _{j=1}^{d-1}g[i-j]$$

最终的答案就是$((f[1][n]-f[0][n])$
为了方便，我们直接开一个二维数组，$f[1][i]$是刚才的$f$，$f[0][i]$是刚才的$g$。

3、代码

#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
const int N = 110;
int f[2][N];
int n, k, d;

void solve()
{
	cin >> n >> k >> d;
	f[0][0] = f[1][0] = 1;
	for(int i = 1; i <= n; i ++ )
	{
		for(int j = 1; j <= k; j ++ )
			if(i >= j)
				f[1][i] = (f[1][i] + f[1][i - j]) % mod;
			
		for(int j = 1; j < d; j ++ )
		{
			if(i >= j)
				f[0][i] = (f[0][i] + f[0][i - j]) % mod;
		}
	}
	cout << ((f[1][n] - f[0][n]) % mod + mod) % mod << endl;
	
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	solve();
}