第一题：环形链表

问题介绍

给你一个链表的头节点head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪next指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回true。否则，返回false 。

问题设置：

链表中节点的数目范围是 [0, 10^4]
-10^5 <= Node.val <= 10^5
pos为-1或者链表中的一个有效索引 。

问题解释：

问题的函数接口传过来的是不带哨兵位的单链表。
可以使用快慢指针来解决。先让快指针和慢指针都指向链表的起始结点，快指针一次走两步，慢指针一次走一步。
如果是带环链表，快指针先进环，慢指针后进环，就成了追及问题。
如果不是带环链表，快指针会走到空，此时结束。

一些问题分析

那为什么快指针一次走两步，慢指针一次走一步，快指针就一定能在环内追上慢指针，和慢指针相遇呢？
当快慢指针都进环后，
最好的情况是，慢指针一进环，就和快指针相遇，程序就结束。
最坏的情况是，慢指针一进环，快指针在慢指针的前一个位置。
假设环内的结点数为N，此时快指针和慢指针相差了N-1步，
因为快指针一次走两步，慢指针一次走一步，每次快指针都比慢指针多走一步，(N-1)的差值会不断减1，直到减为0。
所以慢指针走N-1步后，快指针就会追上慢指针和慢指针相遇。
可以发现：在慢指针进环后，快指针一定可以在慢指针走完一圈之前追上慢指针和慢指针相遇。
那为什么一定是快指针一次走两步，慢指针一次走一步才行，快指针一次走三步，走四步等等不行吗？
首先快指针一次走的步数如果大于两步，循环结束的判断条件会更不好控制是一方面；
同时，像上一个问题分析的，如果慢指针进环后，快指针和慢指针的差距步是N-1，
当快指针一次走三步，慢指针一次走一步，快指针和慢指针每走一次，差距步就缩减两步。
如果N是奇数的情况下，N-1是偶数，(N-1)不断以两步的速度缩减，最终会减为0，也就是快指针追上慢指针和慢指针相遇了
但如果N是偶数的情况下，N-1是奇数，(N-1)不断以两步的速度缩减(也就是：N-1，N-3，…，3，1，-1)；差距步并不能减为0，也就是快指针能追上慢指针，但会和慢指针擦肩而过，直到差距步减为-1的情况出现，快指针又恰好处于慢指针的前一个位置，差距步又恢复为N-1，这就导致在某些极端场景下，出现快指针永远追不上慢指针的问题。

快指针一次走四步等情况，也是类似的道理，就不再赘述。

如果你非要抬杠说，让快指针一次走三步，慢指针一次走两步，进环后差距步也是每次缩减1步，快指针最后也会追上慢指针并和慢指针相遇，不是吗？
那我只能说：对对对，你说得对！

参考代码

bool hasCycle(struct ListNode* head) 
{
    struct ListNode* slow=head;
    struct ListNode* fast=head;

	//因为fast一次走两步，所以需要同时判断fast和fast->next是不是NULL
    while(fast!=NULL&&fast->next!=NULL)
    {
        slow=slow->next;
        fast=fast->next->next;

        if(slow==fast)
        {
            return true;
        }
    }
    return false;
}

第二题：环形链表 II

问题介绍

给定一个链表的头节点head，返回链表开始入环的第一个节点。如果链表无环，则返回null。

如果链表中有某个节点，可以通过连续跟踪next指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数pos来表示链表尾连接到链表中的位置（索引从 0 开始）。如果pos是-1，则在该链表中没有环。注意：pos不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改链表。

问题设置

链表中节点的数目范围在范围[0, 10^4]内
-10\^5 <= Node.val <= 10\^5
pos的值为-1或者链表中的一个有效索引

问题解释

这道题相较上一道题，需要返回带环链表的入环结点。

问题的函数接口传过来的也是不带哨兵位的单链表。

解决这道题需要画图和进行简单的数学分析
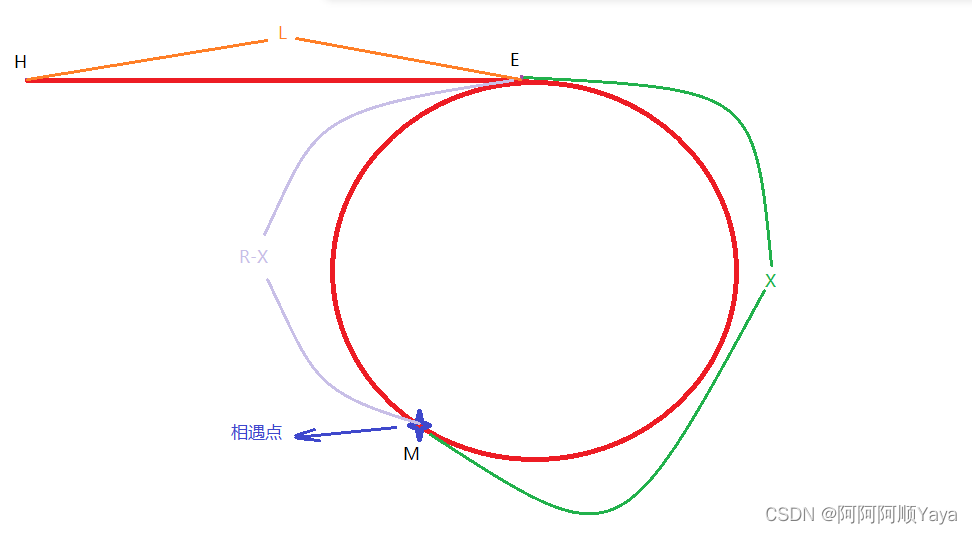
在这里插入图片描述
假设H为链表的起始点，E为入口点，M为相遇点，
H到E的距离为L，环的大小为R，E到M的距离为X，则M到E的距离为R-X

当快指针和慢指针在M点相遇时，
慢指针走过的距离是：L+X；
快指针走过的距离是：L+n*R+X(n>=1)；
在第一题中已经分析：
最好的情况是，慢指针一进环，就和快指针相遇，程序就结束，
此时对于快指针来说，n恰好是1；
最坏的情况是，慢指针一进环，快指针在慢指针的前一个位置，
此时慢指针需要走N-1步，快指针自然要走2倍的N-1步，快指针如果想追上慢指针，就必须先到达入口点E，最终n也可以说是大于等于1的。

但是，这样说未免有失偏颇。
当L很短，而R很大的时候，上述情况可能还说得过；
但如果L很长，R很小，在慢指针还未入环的时候，快指针已经在环内跑了好几圈，这就是另一种情况了。
所以可得出n是大于等于1的。

有了上述的铺垫，可以列出数学等式：
2(L+X) = L+nR+X
=> L+X = nR = (n-1)*R+R
=> L= (n-1)R+R-X

这说明什么呢？
也就是说，有两个指针，一个从H点出发，一个从M点出发，当他们相遇时，他们共同所指的结点就是带环链表的入环结点。
是不是很神奇，下面用代码验证一下吧。

参考代码

struct ListNode* detectCycle(struct ListNode* head) 
{
    struct ListNode* slow=head;
    struct ListNode* fast=head;

    while(fast!=NULL&&fast->next!=NULL)
    {
        slow=slow->next;
        fast=fast->next->next;
		
		//找到相遇点
        if(slow==fast)
        {
            struct ListNode* cur1=head;
            struct ListNode* cur2=slow;

            while(cur1!=cur2)
            {
                cur1=cur1->next;
                cur2=cur2->next;
            }

            return cur1;
        }
    }
    return NULL;
}