目录
- 1、简介
- 2、论文创新点
- 1)倒残差结构 -- Inverted residual block
- 2)ReLU6
- 3、网络结构
文献名称:MobileNetV2: Inverted Residuals and Linear Bottlenecks
发表时间:2018年
下载地址:https://openaccess.thecvf.com/content_cvpr_2018/papers/Sandler_MobileNetV2_Inverted_Residuals_CVPR_2018_paper.pdf
1、简介
Mobile Net V1 存在以下问题:
- 没有残差结构
- 在训练结束后,发现 depth-wise 卷积的很多参数的值都为0,原因有以下3个:
- depth-wise 卷积 权重数量太少; 通道数处理太单薄,只能处理二维信息,没有处理到三维信息
- ReLU 导致小于0的输出都为0,参数也为0
- 移动设备的低精度 数据表示
Mobile Net V2 就以上的问题,做了进一步的改善。
2、论文创新点
1)倒残差结构 – Inverted residual block
ResNet 的 residual block 和 Mobile Net 的 Inverted residual block 的相似与区别:
- 相似: 结构都是
conv 1x1→ \rightarrow →conv 3x3→ \rightarrow →conv 1x1, 最后做一个跨层连接shortcut - 区别:
- residual block 的通道数 是先降后升,而 Inverted residual block 的通道数 是先升后降
- residual block 的中间一层的
conv 3x3是标准的 3x3卷积,而 Inverted residual block 中间一层做的是 depth-wise convolution - residual block 的 shortcut 连接两个高维层(channel 数多的两个层),而 Inverted residual block 连接两个低维层
(有的地方会写 Inverted residual block 跨层连接两个 bottleblock,bottleblock 指的就是通道数少的瓶颈层。) - residual block 每一层后面跟的都是
ReLU 激活函数,而 Inverted residual block 第一个conv 1x1和中间的conv 3x3后面跟的都是 ReLU6 ,最后一个conv 1x1做完降维后,跟的是一个linear 线性激活函数。也就是下图中 对角线斜纹表示的层后面跟的是 线性激活层

Inverted residual block 的结构说明:
- 先做 conv 1x1 ,将 channel 数从 k k k维 升到 t k tk tk 维, t t t是拓展因子(expansion factor)。这一层的计算量是 h × w × k × ( t k ) h \times w \times k \times (tk) h×w×k×(tk)
- 再做 depth-wise convolution,保持 channel 数不变。这一层的计算量是 h × w × ( t k ) × 3 2 h \times w \times (tk) \times 3^2 h×w×(tk)×32
- 最后做 conv 1x1,维度从
t
k
tk
tk 降到
k
′
k'
k′ 。这一层的计算量是
h
×
w
×
(
t
k
)
×
k
′
h \times w \times (tk) \times k'
h×w×(tk)×k′

所以,一个 Inverted residual block 的计算量一共为: h × w × ( t k ) × ( k + 3 2 + k ′ ) h \times w \times (tk) \times (k + 3^2 + k') h×w×(tk)×(k+32+k′)
为什么要使用 倒残差结构呢?
(先说结论再细讲) 因为非线性变换 (ReLU) 会造成信息丢失,所以需要先升维,创造出冗余维度,再在冗余维度中做 非线性变换 (ReLU),最后再把维度降回去,只提取有用的必要信息。
作者做了一个实验,将一个2维空间中 n个点组成的 螺旋线 X 2 × n X_{2 \times n} X2×n, 将其经矩阵 T m × 2 T_{m \times 2} Tm×2 映射到 m 维 ,并做 ReLU激活。表达式为: Y = R e L U ( T m × 2 ⋅ X 2 × n ) Y = ReLU( T_{m \times 2} \cdot X_{2 \times n}) Y=ReLU(Tm×2⋅X2×n)。 再将 Y Y Y 通过 T − 1 T^{-1} T−1 转换回 二维空间,记为 X ^ \hat X X^,对比 X X X 和 X ^ \hat X X^,观察信息丢失情况
** m维 就对应下图中的 dim = 2 / 3 / 5 / 15 / 30
**
T
−
1
T^{-1}
T−1 是
T
T
T 的广义逆矩阵
实验结论是,如果 映射的维度 m比较低,经过ReLU变化后,就会丢失很多信息。 如果 维度m比较高,做ReLU变换后,丢失的信息就少很多。 这也就是为什么 conv 1x1 降维后,不使用 ReLU,而是使用线性激活函数了。

2)ReLU6
为什么采用 ReLU6 呢?
因为 Mobile Net 的设计就是为了应用于 移动设备 或者 内嵌式设备 这种内存比较小的设备上,一般要求低精度表示,比如 使用 8 bit 表示一个数(应该是没有 float8 这种通用数据类型的,这种数据类型用于完全特定目的)。
(以下这句话是个人理解,如有不对请指出)
所以,使用 ReLU6 就可以将数值限制在6之内,整数部分只占3位,剩下的 bit 位 用于表示小数部分,也只能表达较低精度了。 (相关浮点数精度解释 看这里)
那为什么是 6,不是5, 7, 8 呢 ?
作者说 : the value 6 that fits best in 8 bits, which probably is the most use-case.
移动端大多数使用场景采用的是 float8 ,使用 6 是最合适的。
3、网络结构

t :expansion rate
c : 输出的维度数
n : bottleneck 重复的次数
s : (重复的n个模块中)首个模块的步长,剩下的模块步长都为1
其中,block 有的需要跨层连接,有的不要,判断标准是 是否下采样了,下采样的block因为输入和输出尺寸不一样,不能shortcut。只有没有下采样的block(stride=1的block)才有 shorcut。 如下图:
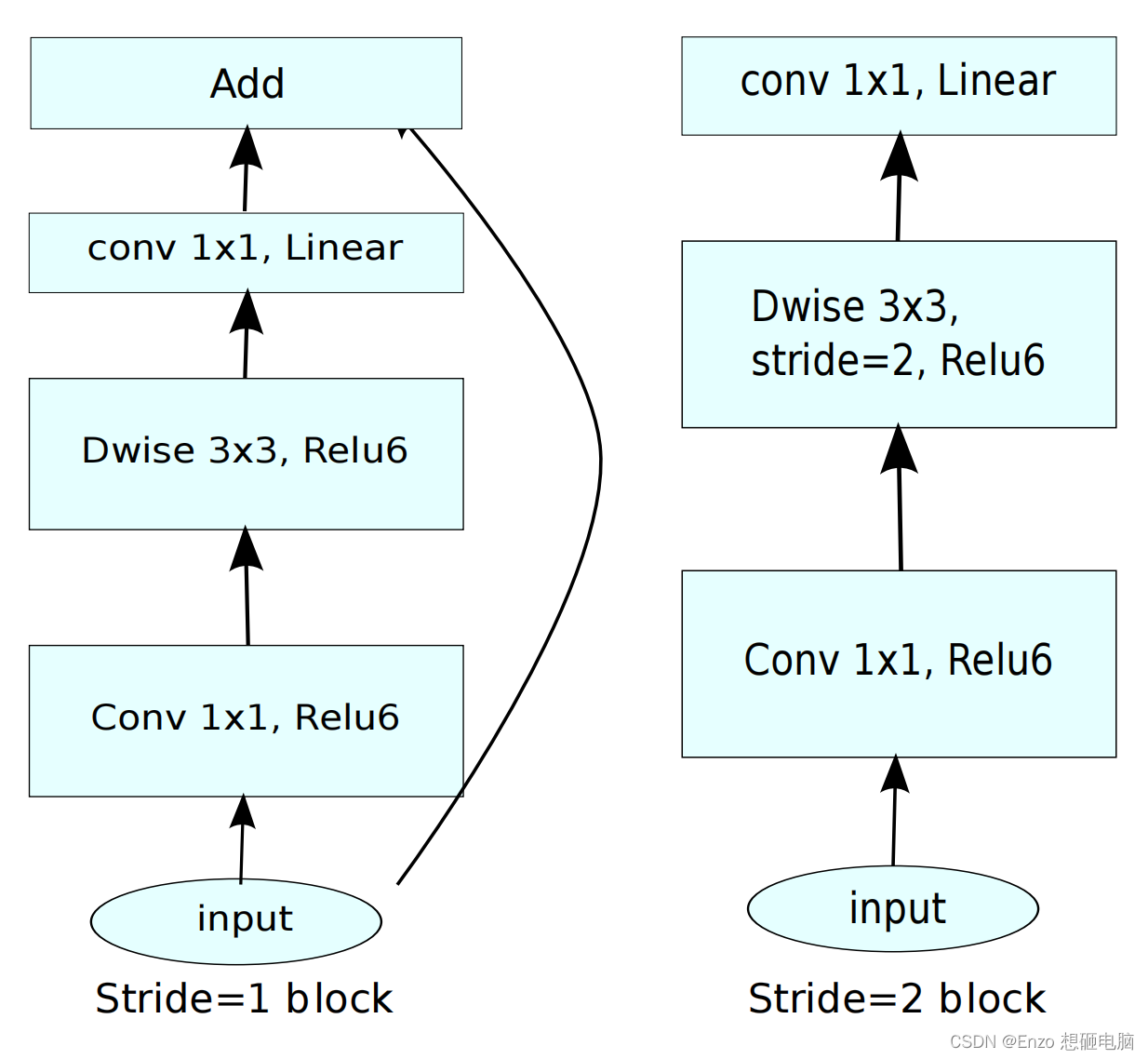
代码地址: