图论在提高组中几乎占据半壁江山,而今天要讲的就是如何存储一个图
一.邻接矩阵
原理
要建立一个图,根本的要素就是边和点
而想要让计算机存储边和点
就需要用到一些数据结构
邻接矩阵是最简单的
他使用了一个二维数组,来表示一个图
假设数组名为map
那么map[i][j]的值就代表i到j的权值
栗子例子:

一个普通的图
注意:一个无向边等于两个有向边,比如1到2权值为1
那么就相当于1->2一条有向边加上2->1一条有向边
一共两条
回归到这个图上
在这里用邻接矩阵的写法就是:
map[1][2]= 3
map[2][1]= 3
map[2][3]= 6
map[3][2]= 6
map[1][3]= 5
map[3][1]= 5
map[5][3]= 2
map[3][5]= 2
map[1][5]= 4
map[5][1]= 4
10条有向边
邻接矩阵原理就是这么简单
代码:
int n,m,vis[100001],mapa[1001][1001],ans=1000000001;
n点 m边 vis点的状态 mapa邻接矩阵二维数组 ans遍历最短距离int main()
{
cin>>n>>m;
int i,j,a,b,c;
memset(mapa,0x3f,sizeof(mapa));
for(j=0;j<m;j++)
{
cin>>a>>b>>c;
mapa[b][a]=c;//保证单向
mapa[a][b]=c;
}
vis[1]=1;
dfs(1,0);
cout<<ans<<endl;
return 0;
}
主函数部分
v[i]=1表示这个点已经走过void dfs(int x,int dis)
{
int i;
if(dis>ans)//小剪枝
return;
if(x==n)
{
ans=min(ans,dis);
return;
}
for(i=1;i<=n;i++) //不一定向前走,可能绕一下更近
if(mapa[x][i]!=0x3f3f3f3f&&vis[i]==0)
{
vis[i]=1;
dfs(i,dis+mapa[x][i]);
vis[i]=0;
}
}dfs主体函数,基础
例题:
暑假小马想到小张家里去玩,他们住在不同的城市,这是小马第一次去小张家,小马提前在百度地图上面查找行车路线,输入出发城市和目的城市,百度地图计算出最短路径,请实现百度地图计算最短路径的方法。备注:总共有n个(n<=100)城市,小马家所在城市编号为1,小张家所在城市编号为n,公路为双向车道。
输入
第一行两个整数,分别表示城市数量n和公路数量m。
后面m行表示公路情况,每一行三个整数a,b,c,分别表示从城市a到城市b,两个城市之间的公路路程c公里。
输出
最短路程公里数
样例输入1
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3
样例输出1
7纯属的模板
其实这题严格来说是最短路径问题
但用来练习邻接矩阵绝对是不二之选
特点及优劣:
优:实在好理解 简单易懂
劣:除了好理解全是劣势 时间复杂度、空间复杂度等等
二.邻接表
邻接表确实有些复杂,但性能还是不错的
1.原理
以点为单位,记录每个点连接的边
数据结构:vector动态数组,动态数组好处就是不需要预估大小,但是会占一些空间

普通小图
首先:与1连接的边共有两条,链表中大概就是这样:



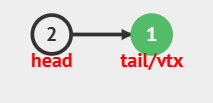


如果没太看懂
没关系
蒟蒻用铅笔画了一下整个过程




就是把n个点看成n个容器,每个容器往里面扔元素
一个元素含义就是一条边,如:1容器中扔了个2,代表1、2之间有边
每个往里面扔的元素,需要有两个参数
第一:边的目标点,也就是例子中的2
第二:边权值
2.代码
int main()
{
node t;
cin>>n>>m;
int i,j,a,b,c;
//memset(mapa,0x3f,sizeof(mapa));//初始化
for(j=0;j<m;j++)
{
cin>>a>>b>>c;
t.v=b;
t.w=c;
e[a].push_back(t);
t.v=a;
t.w=c;
e[b].push_back(t);
}
vis[1]=1;
dfs(1,0);
cout<<ans<<endl;
return 0;
}
e代表容器,因为是vector,一个变量就可以扔无数个元素,所以想要每个点都有只需要一维即可
其他变量名称同邻接矩阵void dfs(int x,int dis)
{
int i;
if(dis>=ans)//小剪枝
return;
if(x==n)
{
ans=min(ans,dis);
return;
}
node tt;
for(int i=0;i<e[x].size();i++)
{
tt=e[x][i];
if(vis[tt.v]==0)
{
vis[tt.v]=1;
dfs(tt.v,dis+tt.w);
vis[tt.v]=0;
}
}
}
就是邻接矩阵的处理上改了一些,但优化了很多很多struct node
{
int v;
int w;
};
vector<node> e[105];
自定义部分,vector动态数组案例依旧是邻接矩阵的1816
3.特点及优劣:
优:解决了时间的问题以及空间的问题
劣:动态数组还是有些差
三。链式前向星
前两个你都不会也没事儿,这个一定要会
1.原理
以边为单位,记录每一条边的目标点,以及权值和下一条边的编号
(1)目标点:还是那个例子1和2之间边权值为3
目标点就为2
(2)权值:不解释了
(2)下一条边的编号:
!!!
链式前向星核心思路来了
链式前向星,顾名思义有链表的成分所在
每条边都有自己的编号
通过编号,层层遍历
还得有一个数组表示以i点为起始点的边的编号
还是画一下
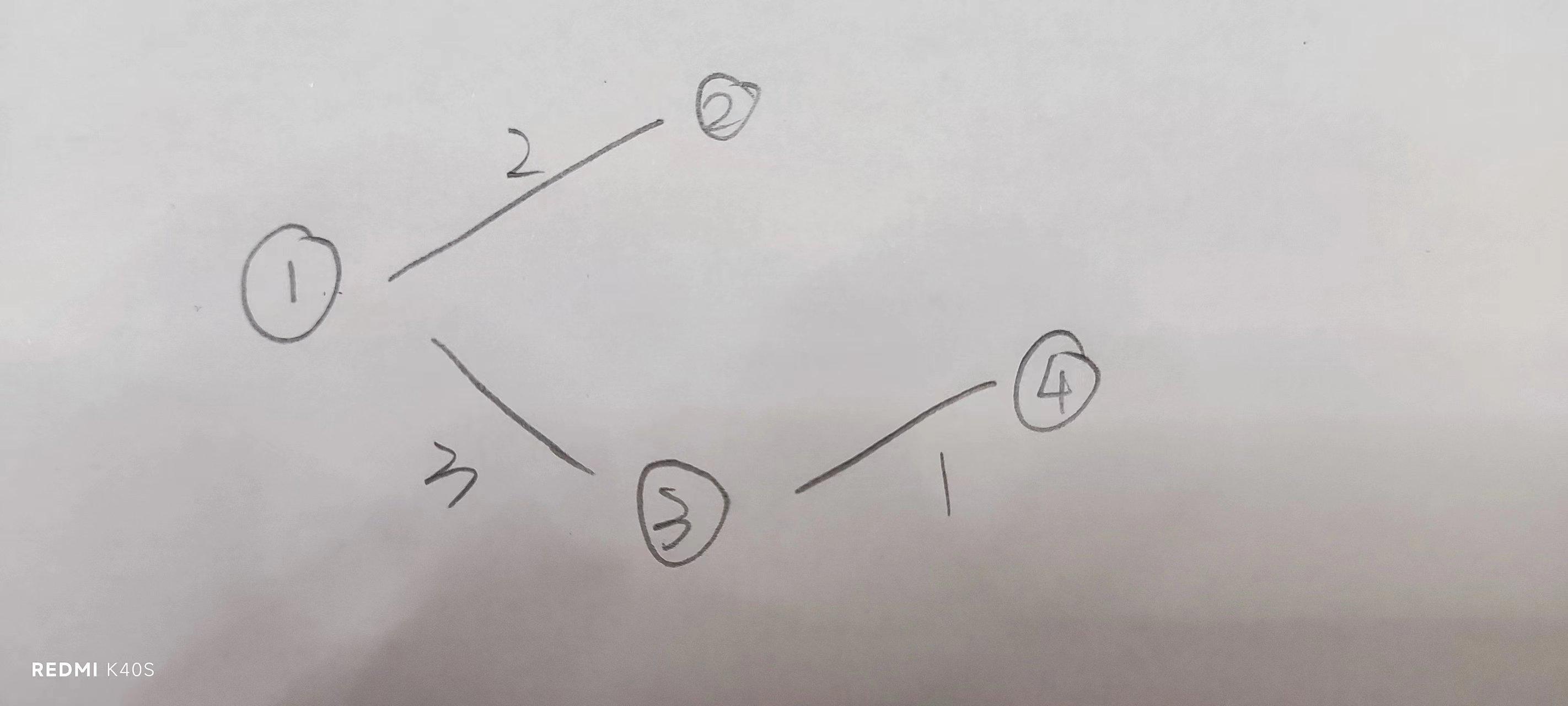
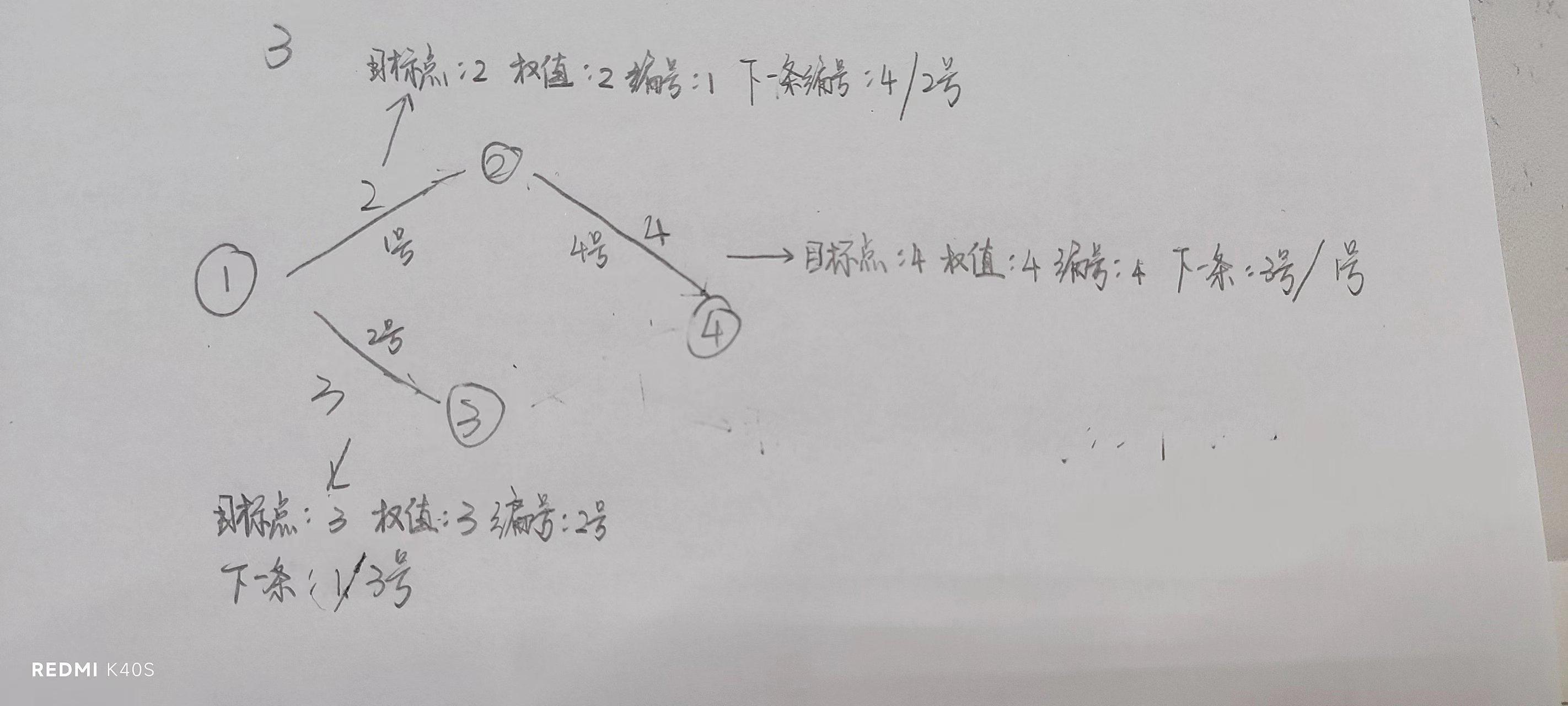
基本思路就是这么个思路,代码也算是比较抽象一些,但懂了之后也很简单
2.代码
int main()
{
cin>>n>>m;
int i,j,a,b,c;
for(j=0;j<m;j++)
{
cin>>a>>b>>c;
addedge(a,b,c);加边操作,一条无向边等于两条有向边
addedge(b,a,c);
}
vis[1]=1;
dfs(1,0);
cout<<ans<<endl;
return 0;
}void addedge(int u,int v,int w)
{
cnt++;边的数量
e[cnt].to=v;目标点初始化
e[cnt].w=w;权值
e[cnt].nxt=h[u];下一条边的编号
h[u]=cnt;以u为起点的边的编号更新
}struct edge
{
int to;
int w;
int nxt;
}e[300];
int cnt;
int h[105];
int n,m,vis[100001],mapa[1001][1001],ans=1000000001;void dfs(int x,int dis)
{
int i;
if(dis>=ans)//小剪枝
return;
if(x==n)
{
ans=min(ans,dis);
return;
}
for(int i=h[x];i>0;i=e[i].nxt)链式前向星遍历方法,h[x]代表以x为起始点的最新的边,只要i还是正数,i作为编号就变成第k条边的下一条边的编号
{
int to=e[i].to;
int w=e[i].w;
if(vis[to]==0)
{
vis[to]=1;
dfs(to,dis+w);
vis[to]=0;
}
}
}特点及优劣
优:时间空间双重解决
劣:需要提前知道边的数量,来定义数组,否则就得用邻接表
以上就是本蒟蒻对邻接矩阵,邻接表,链式前向星的理解了
总结:
邻接矩阵基本没用
有边的数量就用链式前向星,否则就邻接表
看了这么多,点个赞再走才是好习惯doge