将value iteration和policy iteration方法称为model-based reinforcement learning方法，这里的Monte Carlo方法称为model-free的方法。

举个例子

如何在没有模型的情况下估计某些事情？最简单的想法就是Monte Carlo estimation。

举个例子1：投掷硬币

目标是计算$\mathbb{E}[X]$。有两种方法：
Method 1: Model-based

这个方法虽然简单，但是问题是它不太可能知道precise distribution。
Method 2: Model-free
该方法的思想是将硬币投掷很多次，然后计算结果的平均数。

问题：Monte Carlo估计是精确的吗？

• 当N是非常小的时候，估计是不精确的
• 随着N的增大，估计变得越来越精确
  
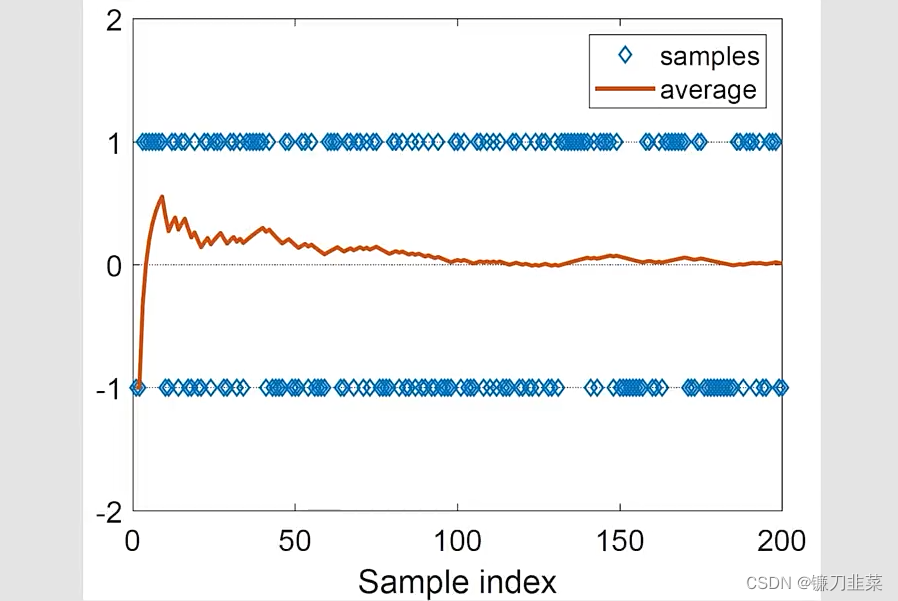
  大数定理（Law of Large Numbers）：
  
  注意：样本必须是独立同分布的（iid, independent and identically distributed）

小结一下：

• Monte Carlo estimation refers to a broad class of techniques that rely on repeated random sampling to solve appriximation problems.
• Why we care about Monte Carlo estimation? Because it does not require the model!
• Why we care about mean estimation? Because state value and action value are defined as expectations of random variables！

The simplest MC-based RL algorithm

Algorithm: MC Basic
理解该算法的关键是理解how to convert the policy iteration algorithm to be model-free

Convert policy iteration to be model-free
首先，策略迭代算法在每次迭代中分为两步：

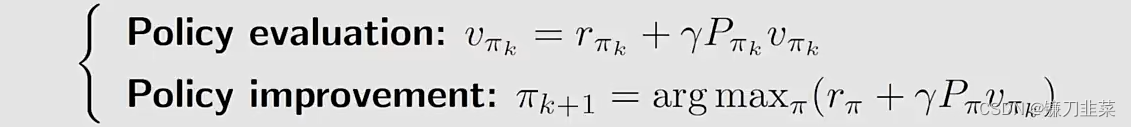
其中policy improvement step的elementwise form如下：

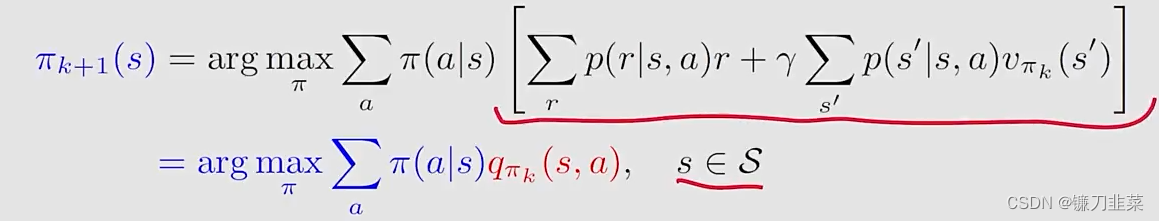
这里的关键是$q_{{\pi }_k}(s,a)$！计算$q_{{\pi }_k}(s,a)$有两种算法：
Expression 1 requires the model:

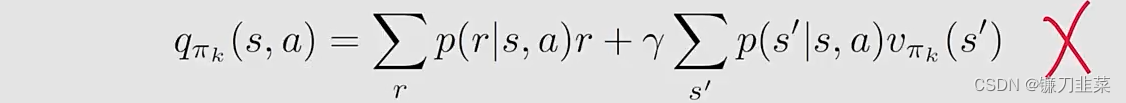
Expression 2 does not require the model：

上面的式子针对实现model-free的RL的启发是：可以使用式子2，根据数据（samples或者experiences）去计算$q_{{\pi }_k}(s,a)$。那具体是怎么做的呢？
The procedure of Monte Carlo estimation of action values：

• 首先，从一个组合$(s,a)$出发，按照一个策略${\pi }_k$，生成一个episode;
• 计算这个episode，return是$g(s,a)$
• $g(s,a)$是在下式中$G_t$的一个采样：$$q_{{\pi }_k}(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$$
• 假设我们有一组episodes和hence { g ( j ) ( s , a ) } \{g^{(j)}(s,a)\} {g(j)(s,a)}，那么$$q_{{\pi }_k}(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]\approx \frac{1}{N}\sum _{i=1}^N{g}^{(i)}(s,a)$$

所以，总的来说，一句话就是当我们没有模型的时候，我们要有数据，反正总得有一个。

到此时，算法也逐渐清晰，这个算法的名称是MC-Basic算法。下面描述这个算法：
给定一个初始策略${\pi }_0$，在第k次迭代有两个步骤：

• Step 1: policy evaluation
  
• Step 2: policy improvemtn
  
  第二步和policy iteration algorithm基本上是一致的，除了上式是直接估计$q_{{\pi }_k}(s,a)$，而不是求解$v_{{\pi }_k}(s)$。

MC Basic algorithm（a model-free variant of policy iteration）的伪代码：

需要注意的是：

• MC Basic算法是policy iteration algorithm的一个变体。
• The model-free algorithms are built up based on model-based ones. 也就是说，在研究model-free算法之前，需要先了解对应的model-based算法。
• MC Basic是非常有用的，它可以揭示MC-based model-free RL的核心思想，但是它并不实用，因为它的efficiency比较低。
• 为什么MC Basic算法估计action values而不是state values?因为state values不能被用来直接改善policies。当模型不可用的时候，应该直接估计action values。
• 由于policy iteration是收敛的，那么很自然地，MC Basic的收敛性也保证了给定足够多的episodes后，它也是收敛的。

举个例子：step by step

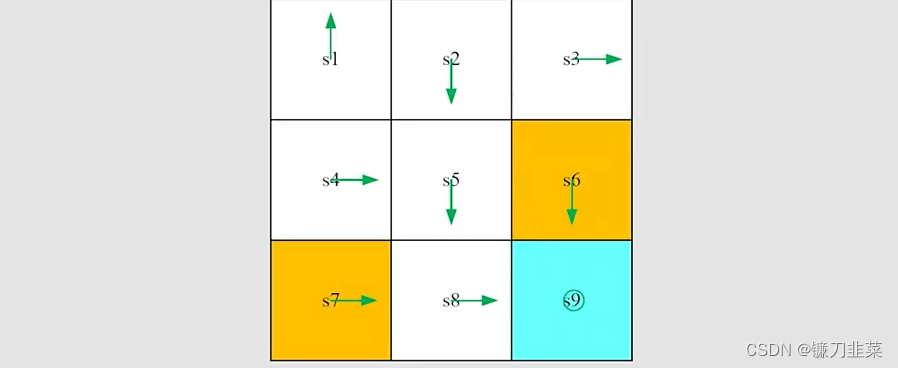
任务是：给定如图所示的一个初始策略，使用MC Basic算法找到一个最优策略，其中$r_{boundary=-1},r_{forbidden}=-1,r_{target}=1,\gamma =0.9$。
MC Basic算法和policy iteration一样，也分为两步。给定当前策略${\pi }_k$

• Step 1 ——policy evaluation: 计算$q_{{\pi }_k}(s,a)$。就这里而言，有多少个state-action pairs呢？一共有9 states × 5 actions =45 state-action pairs。
• Step 2 ——policy improvement: 选择greedy action $$a^{\ast }(s)=arg\underset{a_i}{\max }{q}_{{\pi }_k}(s,a)$$

这里仅仅展示$q_{{\pi }_k}(s_1,a)$：
Step 1-policy evaluation：

• 因为当前策略是确定性的，所以一个episode就可以得到action value!
• 如果当前策略是随机性的，就需要无限个episodes（至少要很多次）。

从$(s_1,a_1)$出发：

从$(s_1,a_2)$出发：

从$(s_1,a_3)$出发：

从$(s_1,a_4)$出发：

从$(s_1,a_5)$出发：

Step 2-policy improvement:

• 通过观察上面的action values，可以看到$$q_{{\pi }_0}(s_1,a_2)=q_{{\pi }_0}(s_1,a_3)$$是最大值。
• 因此，策略可以改进为$${\pi }_1(a_2|s_1)=1\text{ or }{\pi }_1(a_3|s_1)=1$$

不管怎样，新的策略对于$s_1$是最优的。在这个例子中一次迭代就足够了。

举个例子2：Episode length

检查episode长度的影响：

• 需要采样episodes，但是the length of an episode cannot be infinitely long.
• 应该设置多长的episode？

示例设定：一个5-by-5的网格世界，奖励设定为：$r_{boundary=-1},r_{forbidden}=-1,r_{target}=1,\gamma =0.9$
基于不同的episode长度，使用MC Basic去搜索最优策略：


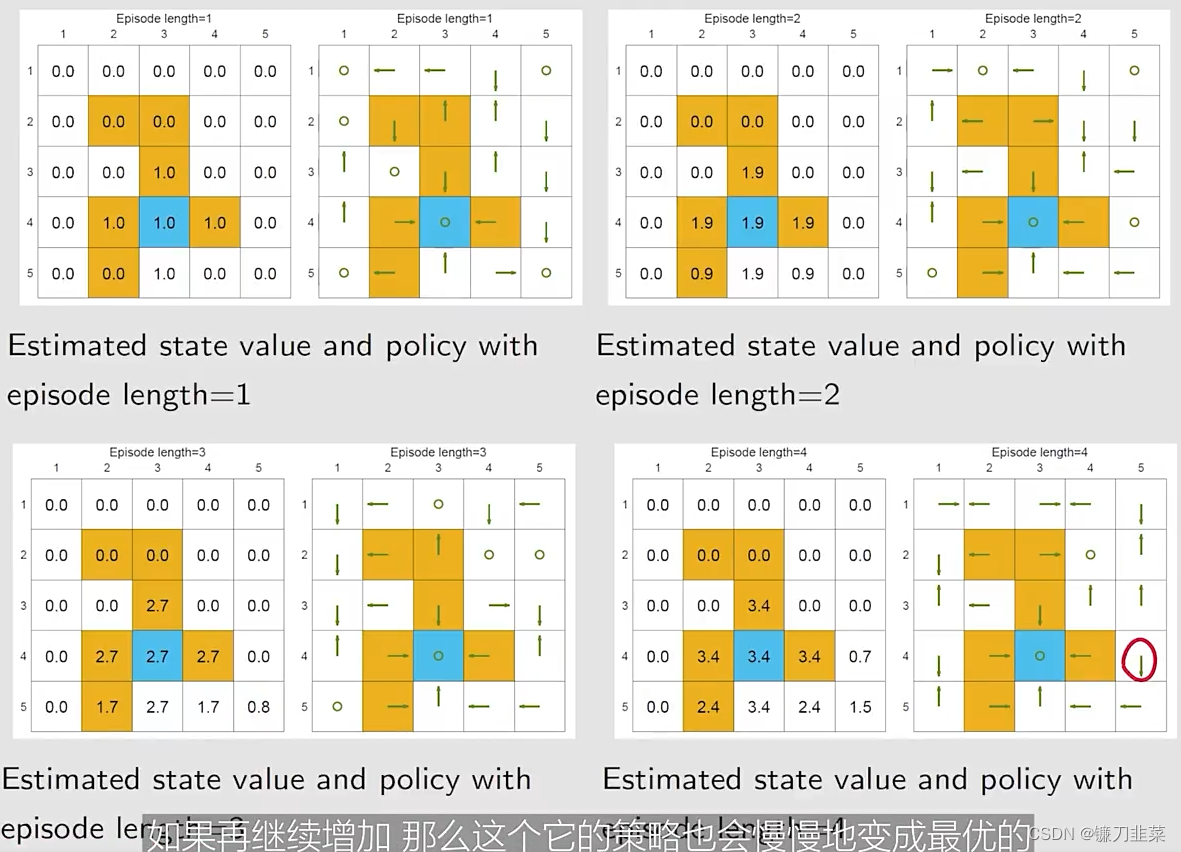
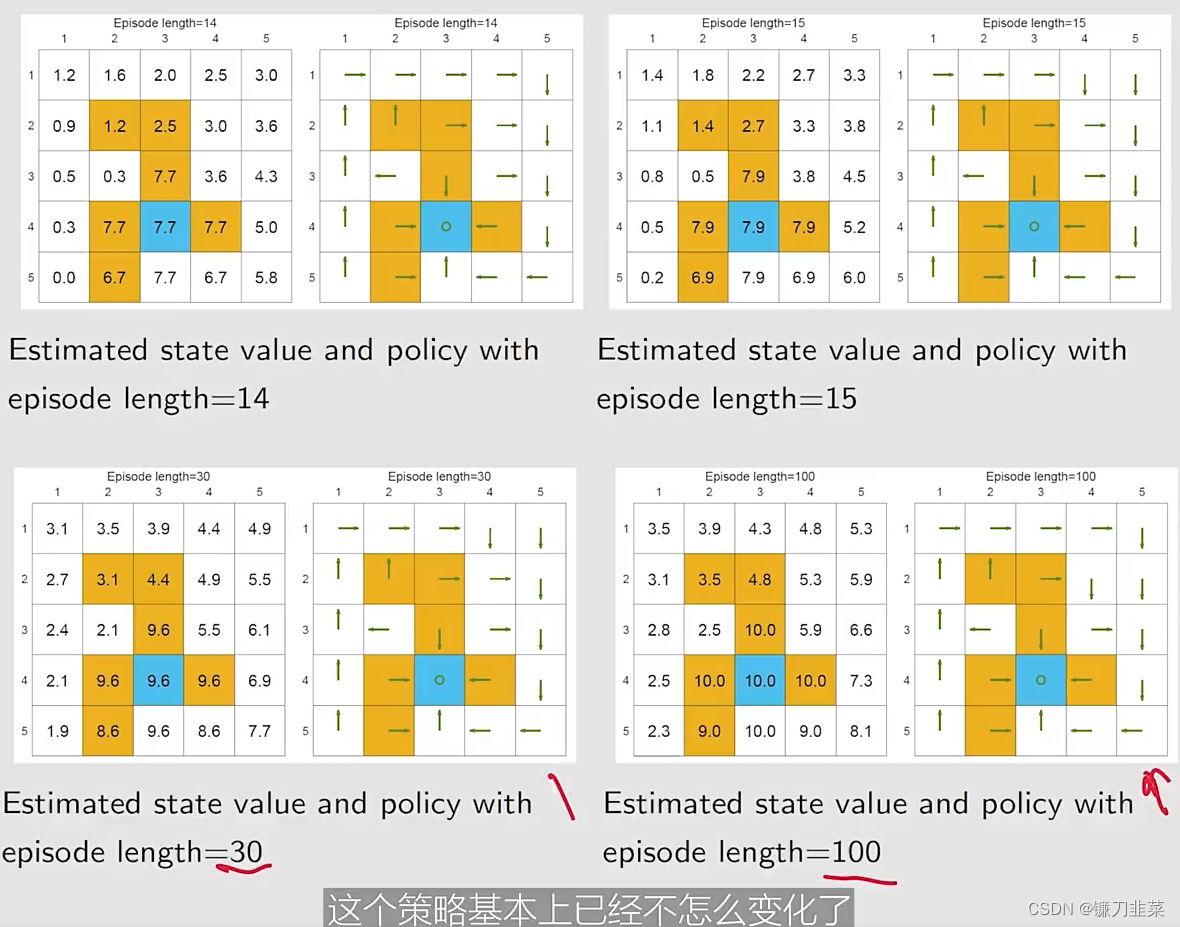
我们的发现：

• 当episode的长度较短的时候，只有离目标较近的状态具有非零的state values。
• 随着episode长度的增加，越靠近target的states更早地变为nonzero values，与那些与target较远的states相比。
• episode length必须要足够长
• episode length也不需要是无限长。

Use data more efficiently

MC Basic算法的优点是清晰地解释了MC方法的核心思想，但是缺点是太简单以至于无法在实际中使用。因此需要将MC Basic算法扩展，使其更加高效。那么如何来做呢？

首先，考虑一个网格世界，根据一个策略$\pi$，得到一个episode，如下：

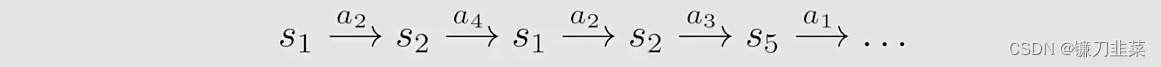
然后，引入一个概念，Visit：every time a state-action pair appears in the episode, it is called a visit of that state-action pair.
在MC Basic算法中用的一个策略是：Initial-visit method。

• 仅仅计算the return和估计$q_{\pi }(s_1,a_2)$
• 这也是MC Basic算法的做法
• 缺点是：不能完全利用数据

充分利用数据：The episode also visits other state-action pairs.

可以估计$q_{\pi }(s_1,a_2)$, $q_{\pi }(s_2,a_4)$, $q_{\pi }(s_2,a_3)$, $q_{\pi }(s_5,a_1)$…
Data-efficient methods:

• first-visit method
• every-visit method

除了怎么样让数据的利用更加高效之外，Another aspect in MC-based RL is when to update the policy。 这里有两个方法：

• 第一种方法：
  
• 第二种方法：
  

那么问题来了，第二种方法会造成一些问题吗？

• 有人会认为一个episode的return不能准确估计相应的action value
• 事实上，we have done that in the truncated policy iteration algorithm，因此，就算不精确，也没有关系.

上述方法的名称是Generalized policy iteration， 简称为GPI:

• 它不是一个特定的具体的算法
• 它表示the general idea or framework of switching between policy-evaluation and policy-improvement processes.
• 许多model-based和model-free RL算法都能fall into this framework。

有了上面的过程，我们可以得到一个新的算法：Algorithm: MC Exploring Starts，即更加高效的使用数据和更新估计。

那么，为什么需要考虑exploring starts？

• 理论上，only if every action value for every state is well explored, can we select the optimal actions correctly. 相反，如果有一个action没有被explored， 那么可能会把这个action漏掉，而它刚好有可能是最优的。
• 实际上，exploring starts是非常难以实现的。对于许多应用，尤其是涉及和环境交互的物理场景中，难以从每一个state-action pair中收集episodes starting。

因此，在理论和实际中存在一个gap。那么能否将exploring starts这个条件去掉，或者转化掉，用其他的形式实现呢？答案是可以的，需要用到soft policies。

MC without exploring starts

什么是Soft policies？如果一个策略采取的每一个action的概率是positive，也就是这些action都有可能被采取，那么这个策略就称为soft。

那么为什么要引入soft policies呢？

• 基于soft policy，a few episodes that are sufficiently long can visit every state-action pair for sufficiently many times.
• Then，我们不需要从every state-action pair得到大量的episodes。因此，上一节中的exploring starts就可以被removed.

那么我们使用什么样的soft policies呢？答案是$ϵ$-greedy policies
什么是$ϵ$-greedy policy？

这里有一个性质，就是选择这个greedy action的概率始终比其他的任何一个action的概率都要大。

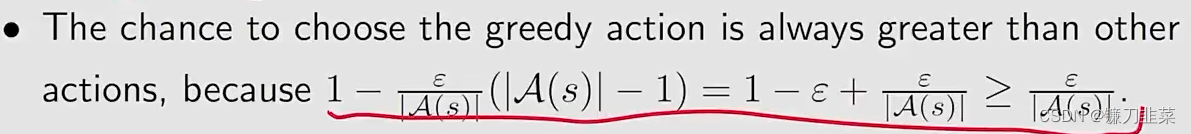
为什么要使用$ϵ$-greedy？因为它能够平衡exploitation（充分利用现有的）和exploration（探索未知的）。

• 当$ϵ=0$，它变为了greedy！与exploitation相比，exploration就会弱一些！
• 当$ϵ=1$，它变为了一个均匀分布，exploration更强，exploitation更弱。

那么如何将$ϵ$-greedy整合到MC-based RL算法中呢？
之前在MC Basic和MC Exploring Starts中policy improvement step是求解：

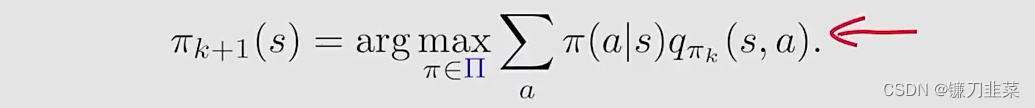
其中的$\Pi$表示所有可能的选择的集合。求解出来的最优的策略是：$${\pi }_{k+1}(a|s)=\{\begin{array}{ll}1& a=a_k^{\ast }\\ 0& a\ne a_k^{\ast }\end{array}$$其中$a_k^{\ast }=\text{arg}{\max }_a{q}_{{\pi }_k}(s,a)$
现在，the policy improvement step变为求解：

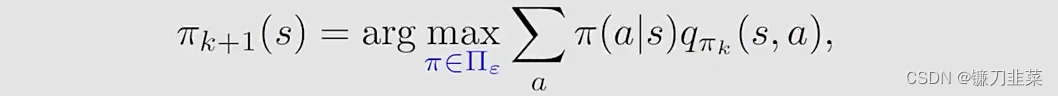
其中${\Pi }_{ϵ}$表示在一个固定的$ϵ$值条件下的所有$ϵ$-greedy policies的集合。这时得到的最优策略是

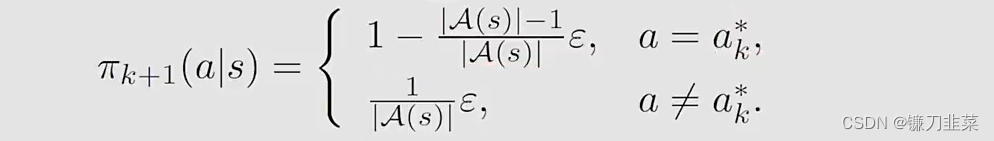
实际上，这里就得到了MC $ϵ$-greedy算法，与MC Exploring Starts算法相同，除了MC $ϵ$-greedy算法使用$ϵ$-greedy策略。因为使用这样一个策略，就不需要exploring starts这样的条件了，但是仍然要求visit all state-action pairs in a different form。

Algorithm: MC $ϵ$-Greedy的伪代码

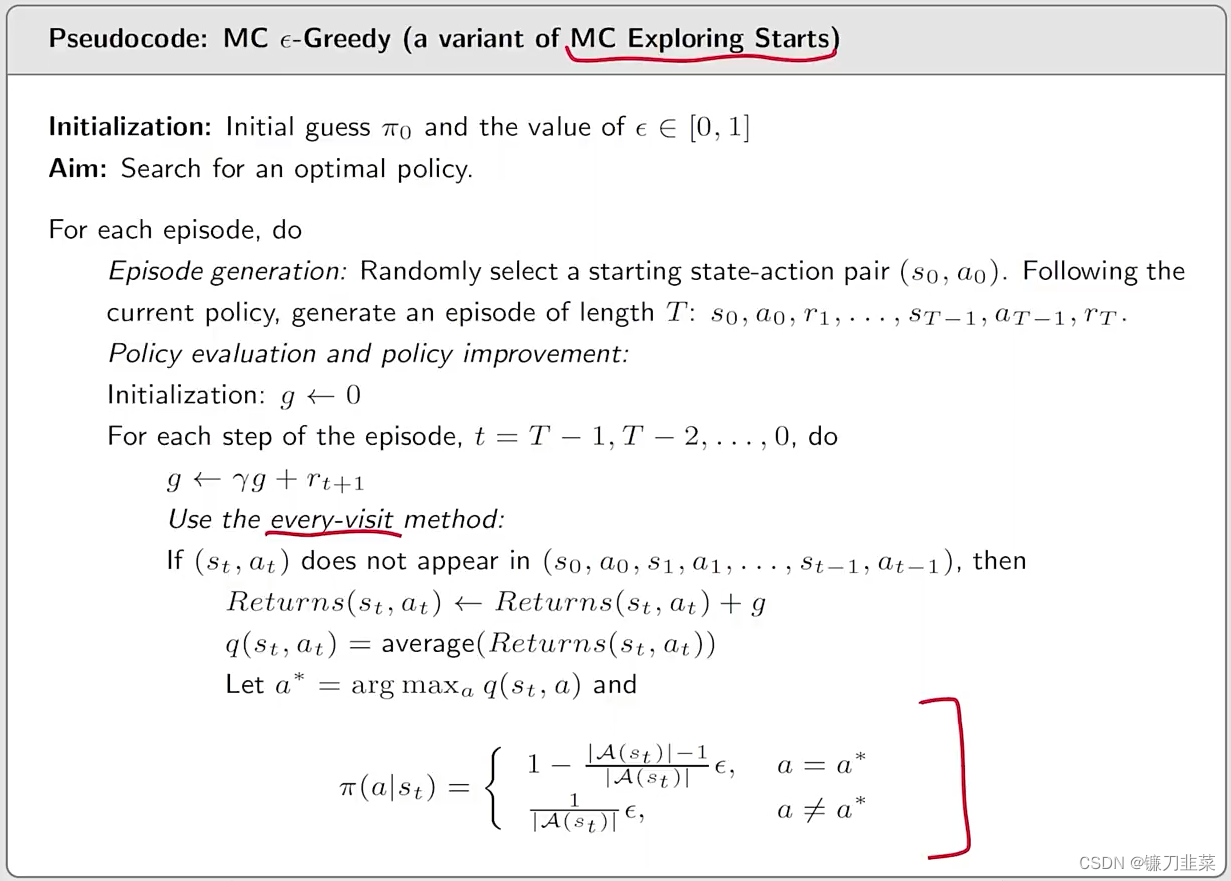
现在，我们分析该算法的探索能力，一个单独的episode可以visit所有的state-action pairs吗？
当$ϵ=1$，the policy（均匀分布）具有最强的探索能力。

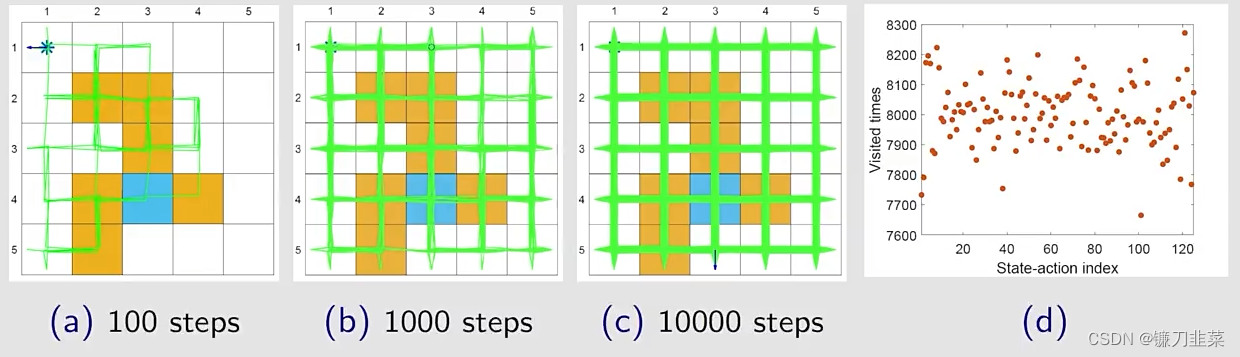
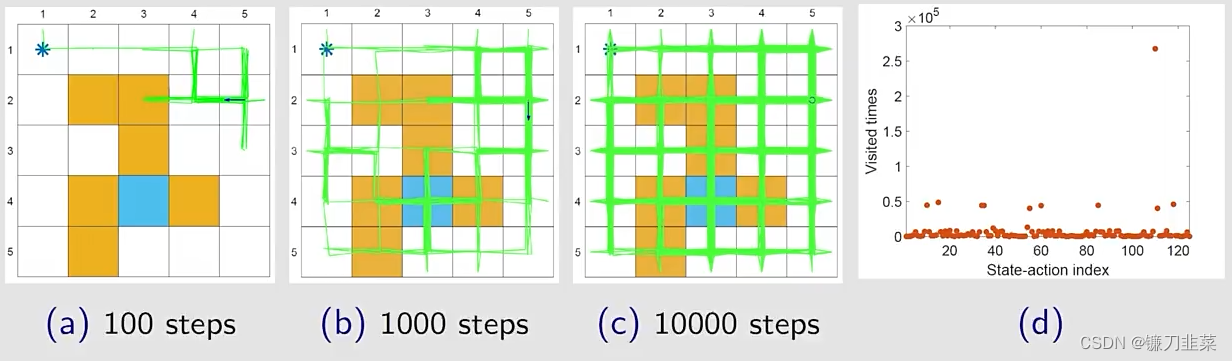
随着步数的增加，网格中几乎所有的位置都探索到了（绿色线），每个state-action被访问的次数也比较高。
当$ϵ$比较小的时候，策略的探索能力也会弱一些。

举个例子：利用$ϵ$-greedy结合蒙特卡洛算法，看一下这个算法能够带来什么样的最优策略。
在每一个iteration中：

• 在episode generation step，用当前的$ϵ$-greedy策略生成一个episode，这个episode非常长，只有100万步。
• 然后，用这一个episode去更新剩下所有的state-action pair和policy
• 这个算法避开了exploring starts这样一个条件，只要episode足够长，即使它从一个state-action pair出发，它仍然能够访问所有的其他的state-action pair。

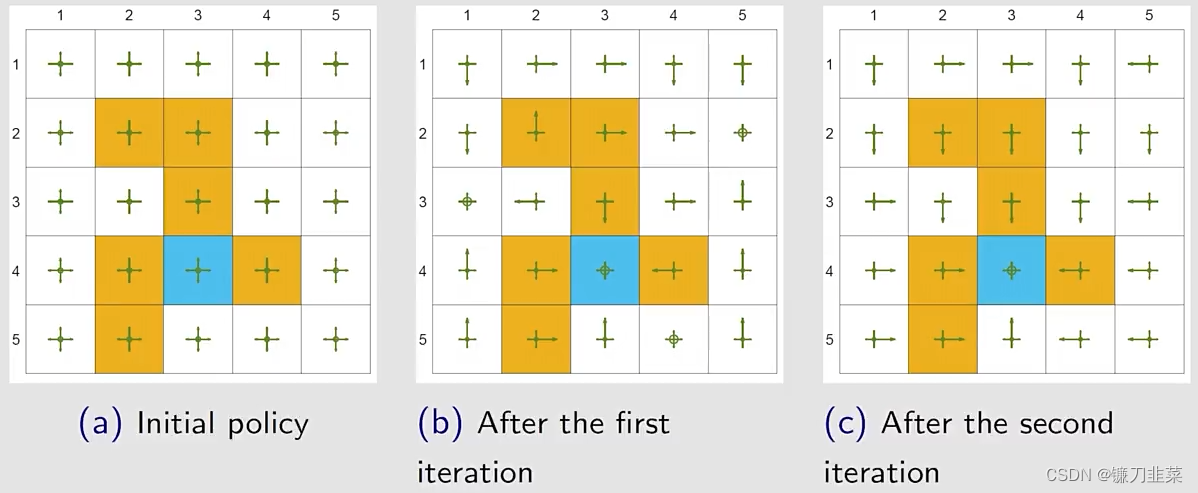
这里$r_{boundary=-1},r_{forbidden}=-10,r_{target}=1,\gamma =0.9$，两次迭代就得到了一个optimal $ϵ$-greedy policy。所以$ϵ$-greedy通过探索性得到了一些好处，但是牺牲的是它的最优性。实际使用中，设置一个比较小的$ϵ$值，当它趋向于0的时候，$ϵ$-greedy接近于greedy，所以此时找到的最优的greedy的策略也就接近最优的greedy的策略。实际当中也可以让这个$ϵ$逐渐减小。

接下来，通过例子证明这个过程，设定为$r_{boundary=-1},r_{forbidden}=-10,r_{target}=1,\gamma =0.9$。
最优性（Optimality）：
给定一个$ϵ$-greedy policy，它的state value是什么？

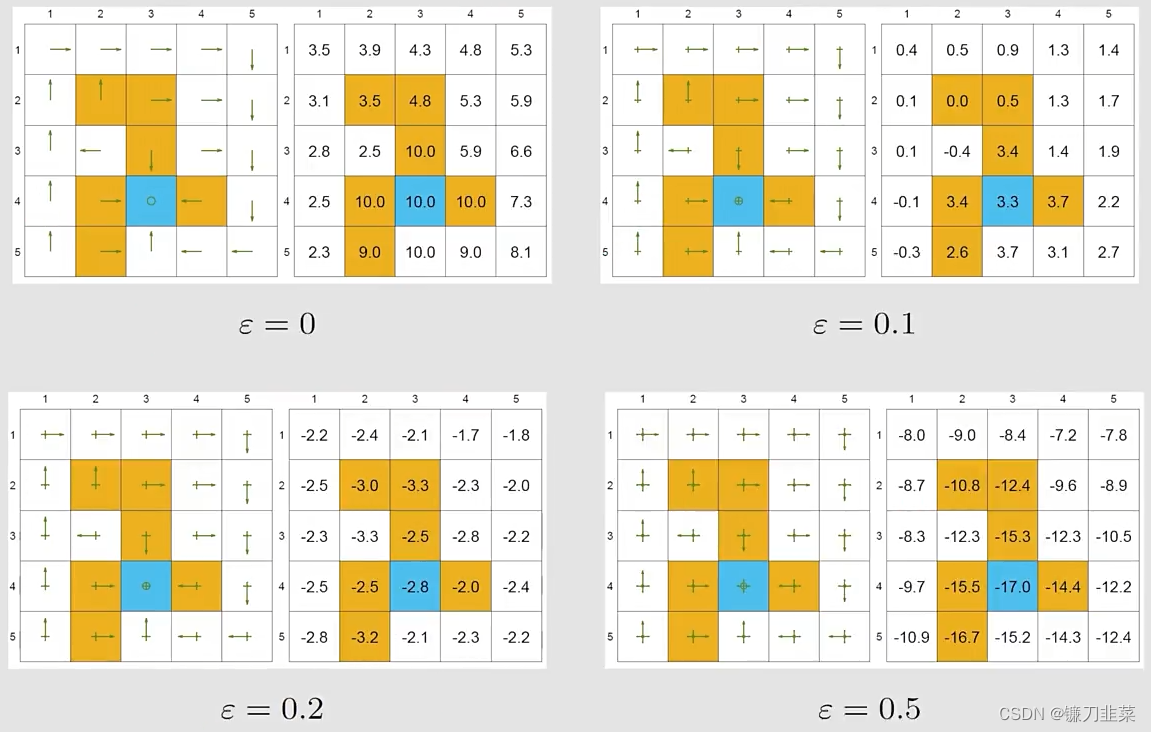
最优的策略就是有最大的state value的策略。当$ϵ$增加的时候，the optimality of the policy becomes worse! 为什么目标state的state value变为了negative？因为它在这个地方有比较大的概率进入到forbidden area，得到负数的reward会非常多。

一致性（Consistency）：
找到最优的$ϵ$-greedy policies和它们的state values？直接给出一个最优策略，用MC $ϵ$-greedy 算法，设置$ϵ$为0.1。一致性也就是当$ϵ$-greedy得到的策略与greedy得到的策略是一致的。

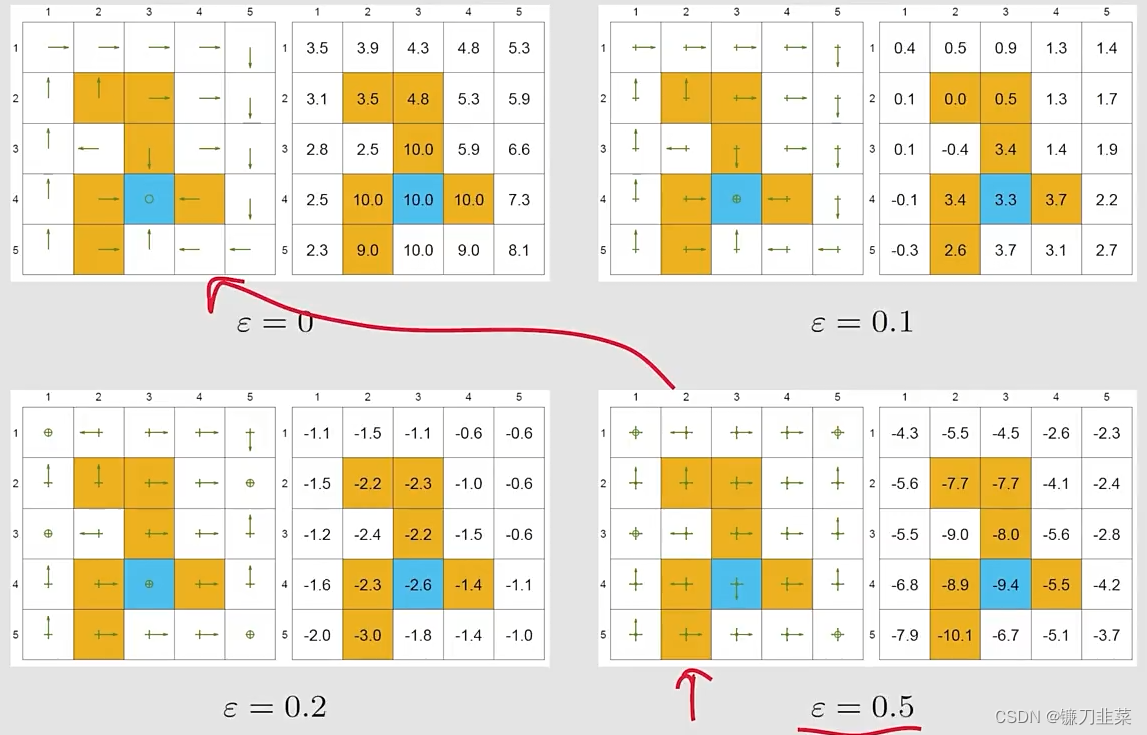
结论是如果想用 MC $ϵ$-greedy的时候，$ϵ$不能太大。从探索性比较大，逐步减小$ϵ$，最终得到一个最优的策略。

总结

关键点：

• 基于Monte Carlo方法的Mean estimation
• 三个算法：
  • MC Basic
  • MC Exploring Starts
  • MC $ϵ$-Greedy
• 这三个算法之间的关系
• $ϵ$-greedy policies的最优性和探索性

内容来源

1. 《强化学习的数学原理》 西湖大学工学院赵世钰教授
2. 《动手学强化学习》 俞勇 著