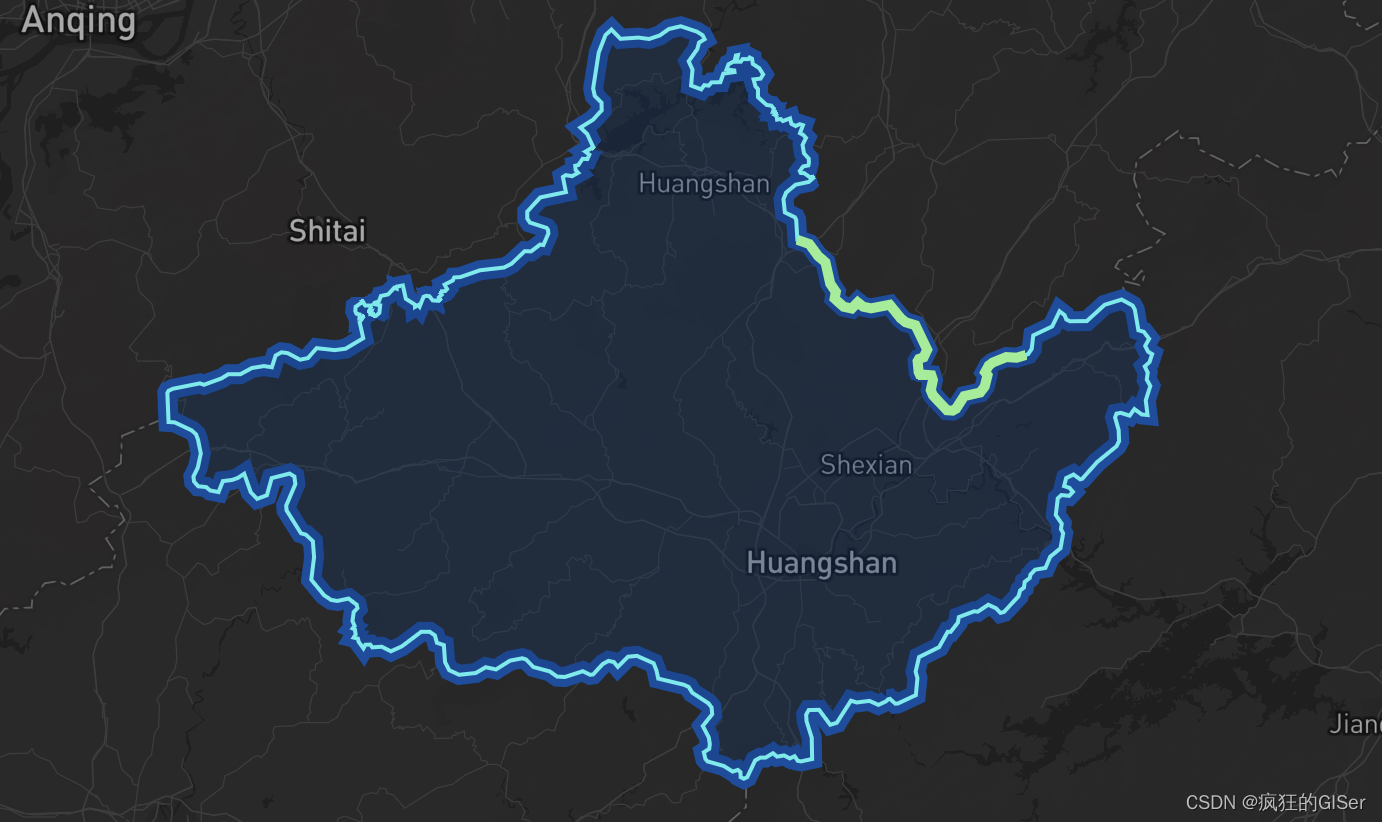
AI+Science专栏由百度飞桨科学计算团队出品,给大家带来在AI+科学计算领域中的一系列技术分享,欢迎大家关注和积极讨论,也希望志同道合的小伙伴加入飞桨社区,互相学习,一起探索前沿未知。
作为系列分享的第一篇,本文内容涵盖行业背景与痛点、AI+科学计算领域的前沿算法、基于飞桨的AI+科学计算产品方案、涉及的飞桨框架关键技术以及PINNs方法求解计算流体力学方腔流的案例等。
行业背景与痛点
当前AI技术在CV、NLP等领域已有了较为广泛的应用,替代传统方法完成缺陷检测、人脸检测、物体分割、阅读理解、文本生成等任务,在产业界也形成了规模化的落地。但是放眼到更加广阔的工业设计、制造等领域,仍有诸多科学和工程问题亟待解决。比如对于高层建筑结构、大跨桥梁、海上石油平台、航空飞机等,流体和结构的复杂相互作用会引起动力荷载,进而导致抖振、涡振、驰振、颤振等流致振动,影响结构安全与服役年限。数值模拟是研究工程结构流致振动的有效方法之一,但是传统数值方法需要大量的计算资源,在计算速度上有很大的局限性等等。
AI+科学计算领域 前沿算法与典型应用案例
上述的问题指向了AI+科学计算的发展: 利用深度学习技术突破维数高、时间长、跨尺度的挑战,改变科学研究范式,帮助传统行业转型。提到AI方法,大家直观的印象是大数据、神经网络模型搭建与训练。在CV,NLP等领域中也确实如此,AI方法以数据驱动,训练出神经网络以模拟图像分类、语音识别等实际问题中隐含的复杂逻辑,整体是一个“黑盒”问题。但在解决科学计算相关问题上,使用的AI方法有所变化,除了使用纯数据驱动方法解决问题外,有时候还需要加入一些物理信息约束,因此,需要更多的领域相关知识。
具体来看,在科学计算领域,往往需要针对海洋气象、能源材料、航空航天、生物制药等具体场景中的物理问题进行模拟。由于大多数物理规律可以表达为偏微分方程的形式,所以偏微分方程组的求解成为了解决科学计算领域问题的关键。神经网络具备“万能逼近”的能力,即只要网络有足够多的神经元,就可以充分地逼近任意一个连续函数。所以使用AI方法解决科学计算问题的一个思路是训练神经网络以模拟某个偏微分方程组的解函数。
使用AI 方法解决科学计算问题,相对传统方法有一些潜在的优势:
(1)高维问题处理优势
传统方法一般是基于有限差分、有限元、有限体积等方法,求得偏微分方程组的近似解。这些方法面临着“维度灾难”,即计算量随着维度增加快速增长。在AI方法的神经网络中,维度增加带来的计算量增加是线性的。
(2)硬件加速优势
传统方法由于存在串行运算,往往难以使用GPU等硬件进行加速。AI方法中的训练和推理过程都比较容易发挥GPU等硬件优势。
(3)泛化优势
AI方法解决问题分为训练和推理两个过程,一次训练,多次推理。借助神经网络的泛化能力,在某些物理参数条件下训练出的网络,在其他物理参数下也可以获得很好的模拟效果。
AI+科学计算领域中最著名的方法是PINNs(Physics-informed neural networks)方法,该方法提出一种新的复合型的损失函数,由偏微分方程组部分,边界条件部分,初始条件部分三部分组成。
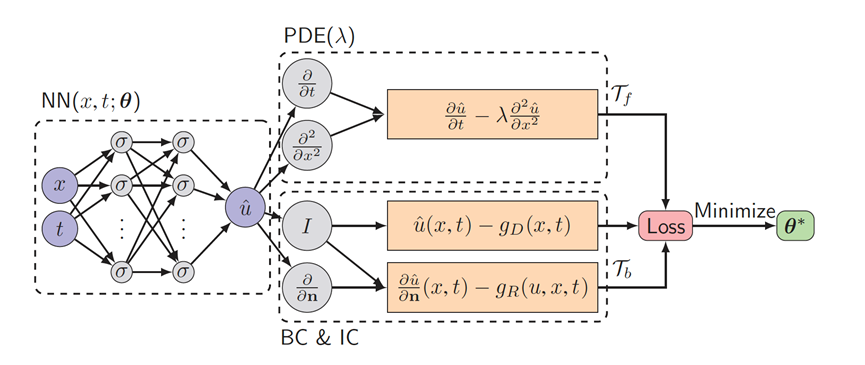
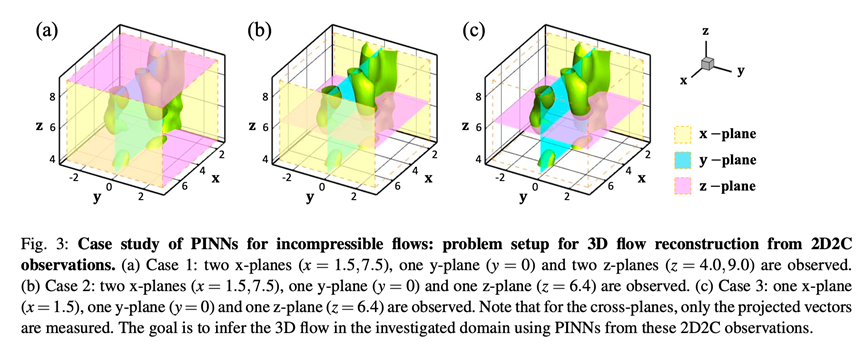
由于加入了物理信息约束,该方法在没有任何输入数据的情况下,只指定边界条件和初始条件,就可以训练出神经网络拟合目标PDE的解。也有一些学者在原始PINNs方法的基础上进行改进,加入一些数据,形成偏微分方程部分、边界条件部分、初始条件部分、数据部分4部分组成的损失函数,进一步提高神经网络的模拟精度,在3D不可压的流体问题上取得了不错的结果。如下图所示,分别对三种不同case使用PINNs算法基于二维二元观察速度进行了3D流场重建,并计算了三种case中不同方向速度及压力的L2范数相对误差。可以发现PINNs方法可以精准捕捉漩涡脱落的不稳定性。
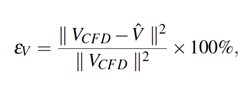
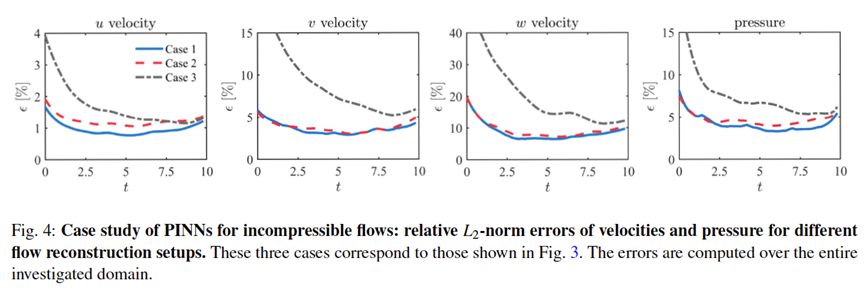
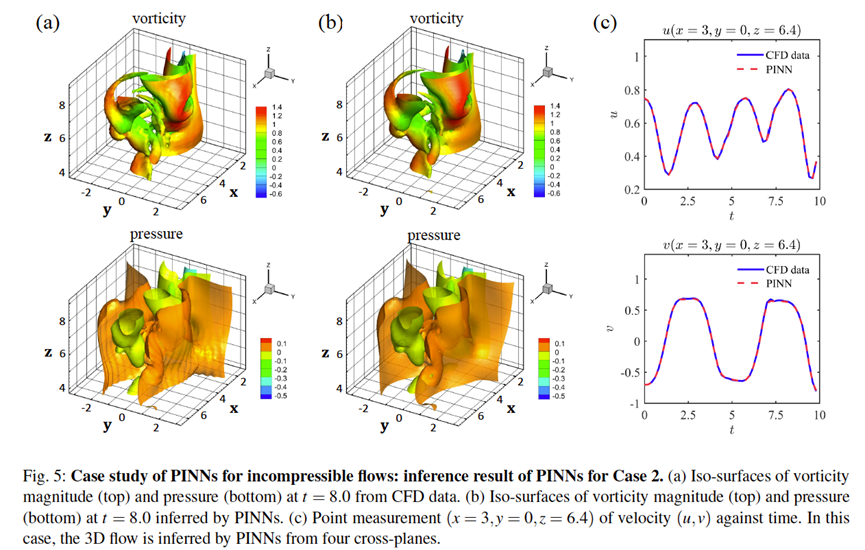
总体而言,AI为科学计算问题的解决提供了新的研究范式,无论是AI完全取代传统方法,还是AI与传统方法融合的相关工作都在快速发展,未来会更大程度地影响整个科学计算领域,成为新一代革命性的方向。
基于飞桨的 AI+科学计算产品方案
飞桨科学计算开发套件以开源深度学习框架飞桨为核心,结合科学计算领域专有知识,搭配高性能的基础设施异构平台,提供给科研开发者简单易用的AI+科学计算产品方案。
百度飞桨在2021年12月正式发布飞桨科学计算套件 0.1版本,依托底层核心框架在高阶自动微分功能上的技术革新,快速高质量推进飞桨在AI+科学计算领域的能力建设。
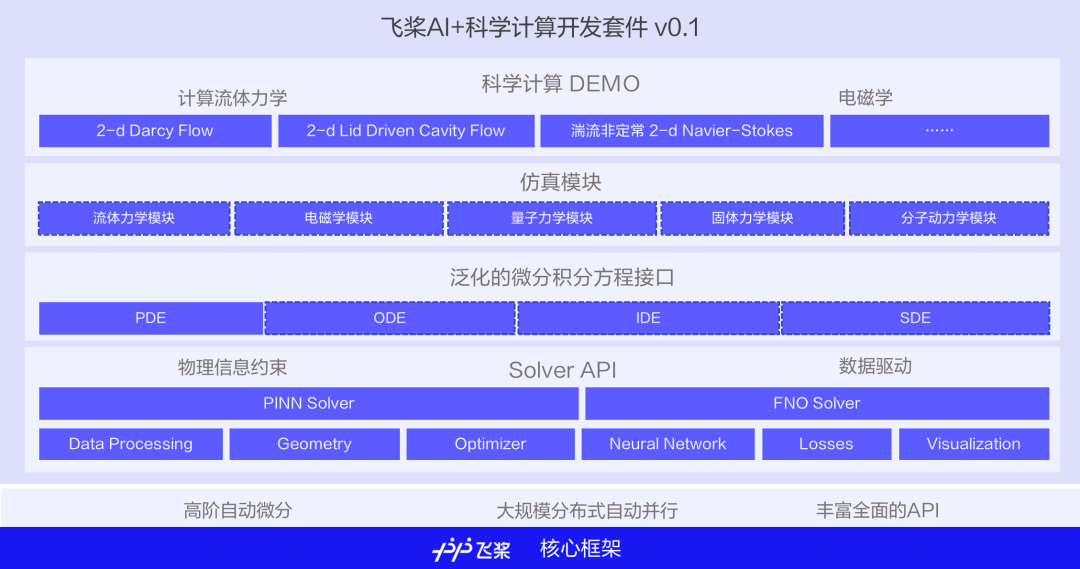
飞桨科学计算套件提供泛化的微分、积分方程等接口以及两种求解器PINNs(物理信息神经网络)和FNO(傅立叶神经算子),支撑上层应用各种微分、积分方程的求解。并且我们正在开展生态共建,联合打造多个跨领域的仿真模块,并针对各个模块开发典型应用案例。飞桨科学计算套件目前已提供达西流(Darcy Flow)、顶盖方腔流(Lid-driven Cavity Flow)等计算流体力学领域的经典算例。
支撑科学计算的 框架关键技术
飞桨科学计算开发套件整体依托于飞桨核心框架,为了支持科学计算类任务,飞桨核心框架新增了函数式自动微分接口和部分算子高阶自动微分的功能。
自动微分机制是广泛应用于深度学习框架之中微分技术。区别于符号微分和数值微分,自动微分依托深度学习框架中的计算图,在每个计算图节点内进行符号微分,并把节点间的微分结果用数值存储,进而实现比数值微分更精确,比符号微分更高效的微分机制。
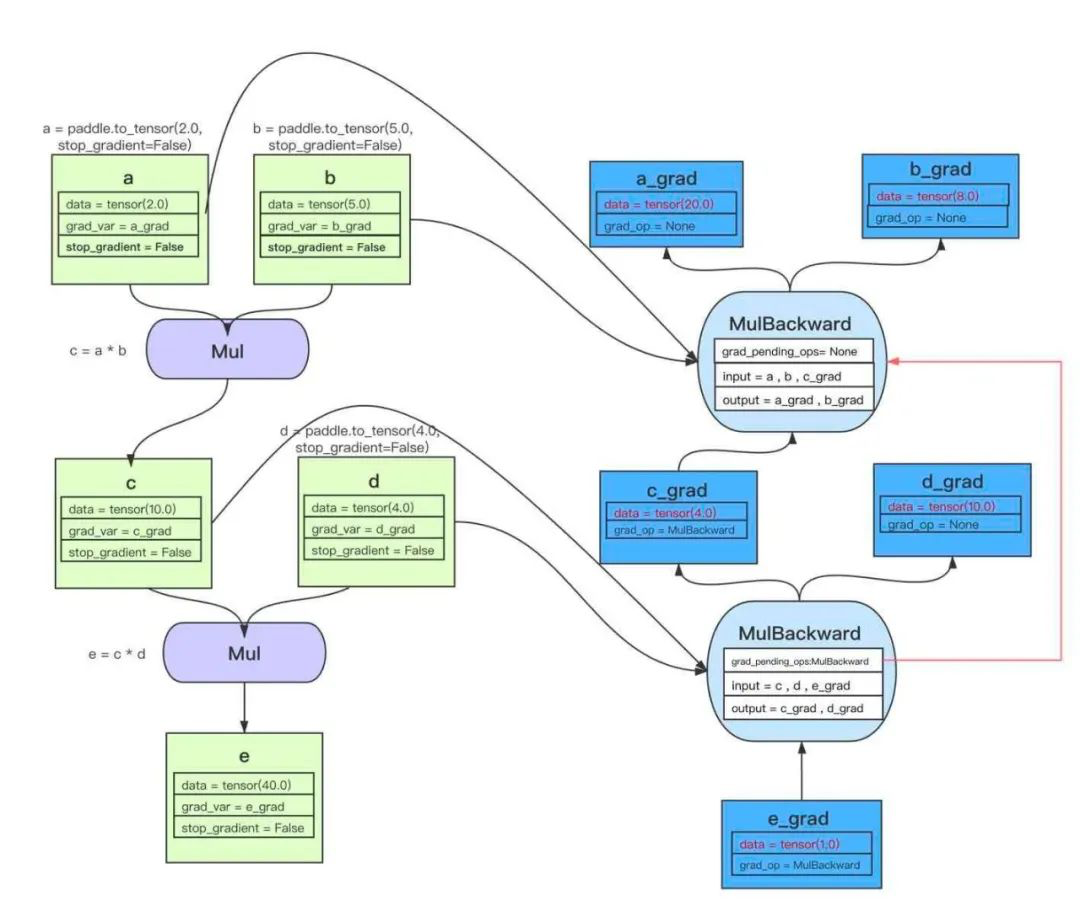
相比传统AI任务,科学计算任务对框架提出了新的需求:(1)由于损失函数中存在方程部分,功能上要求支持更高阶的微分;(2)在用户接口上,需要提供更加贴近数学公式的函数式自动微分接口。
为了支持高阶微分,我们一方面在框架中增加高阶导数算子,另一方面也在设计基础算子体系,支持不限阶数的自动微分。
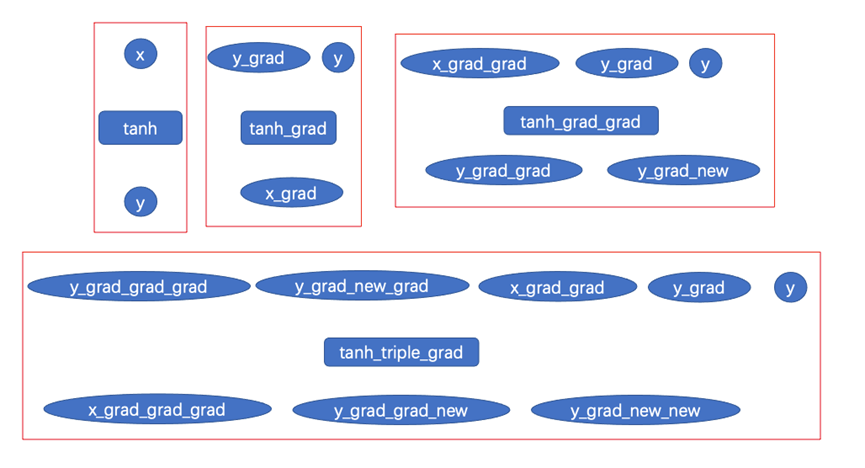
在自动微分接口方面,我们提供 jacobian,hessian,jvp,vjp等函数式自动微分接口,让用户可以用更加自然的方式完成方程构建。
案例介绍: PINNs方法求解计算流体力学 顶盖驱动方腔流
Lid-driven Cavity Flow(顶盖驱动方腔流)是CFD(计算流体力学)领域中一个经典benchmark问题,常用于验证计算方法,我们选择了这个问题作为CFD领域中第一个典型应用案例。顶盖驱动方腔流中包含一个充满液体的方形腔体。这个腔体三面封闭,顶部开放,顶部有水平方向的速度用来驱动方腔内的流体流动,其他三个腔壁为无滑动边界,速度为零。在这个问题下,我们需要求解稳态不可压缩的Navier-Stokes方程。
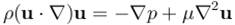
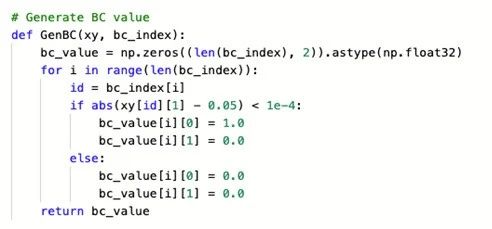
其中u为顶盖速度,ρ为流体密度,p为压力。首先我们在二维区域内选定计算域,构成正方形,并在x、y两个方向上进行离散选点。对四个壁面的边界条件定义如下:
我们拟定顶盖初始速度为1,雷诺数为10的情况下,使用PINNs方法对方腔内流场进行模拟。我们求解定常NS方程,设定自变量空间坐标(x, y)作为PINNs网络的输入,网络的输出为流场中在x,y两个方向的速度(u, v)。损失函数定义为控制方程的损失函数与边界条件的损失函数乘以各自权重并相加。神经网络通过梯度下降反向传播等机制,将损失函数数值收敛到最小,因此将NS方程求解问题转化为优化问题。
神经网络loss定义:

调用PINNs求解器设置训练参数:

预测流场速度(u, v)并转化为vtk文件进行可视化:

结果展示:
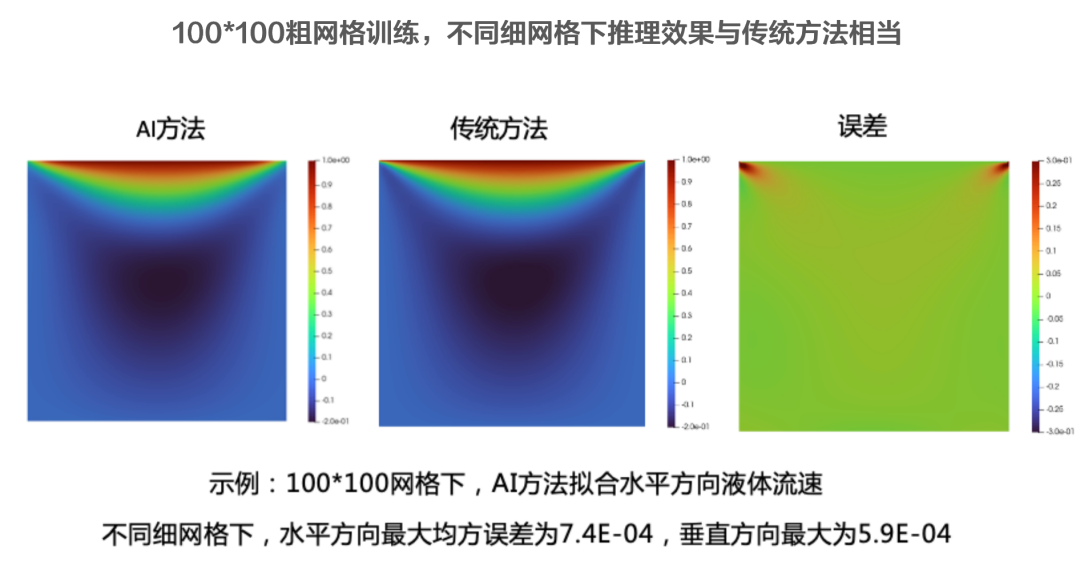
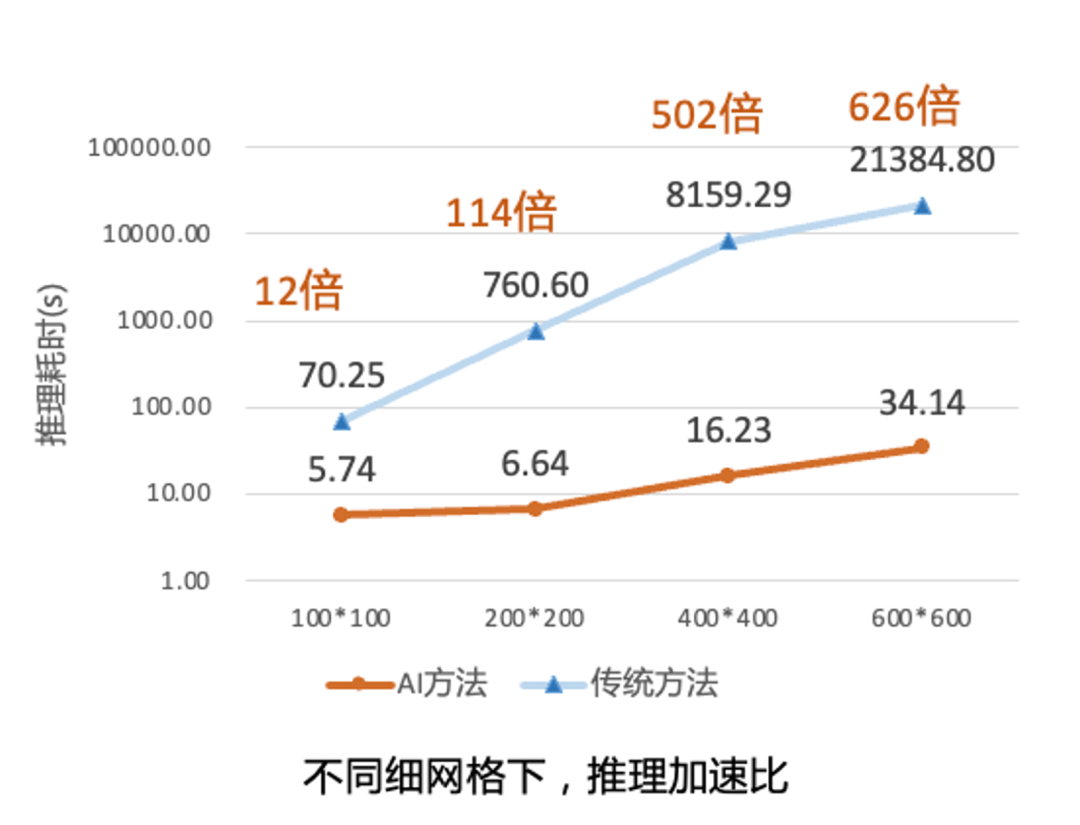
在低雷诺数下,流体粘性起到很大作用,在方腔的左右下方两个边角还未形成明显的涡,速度梯度均匀。在PINNs方法下,和传统方法(OpenFOAM)结果对比水平方向最大均方误差为7.38R-04,垂直方向最大均方误差为5.99E-04。推理计算量和网格呈线性关系,推理速度大于传统方法的12~626倍。
飞桨科学计算套件Github:
https://github.com/PaddlePaddle/PaddleScience