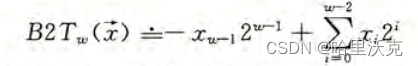本章重点纲要
目录
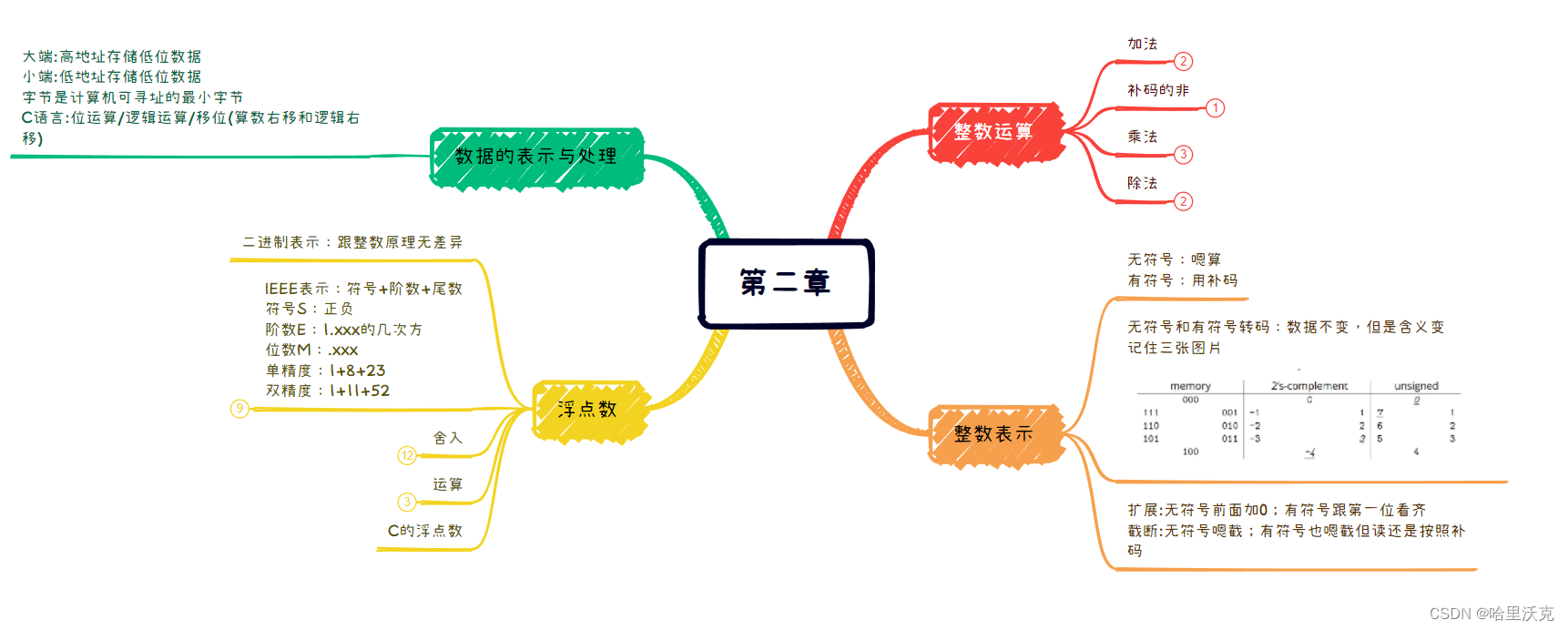
2.1 数据存储
2.1.1 进制
2.1.2 数据在内存的存储方式---大小端
2.1.3 C语言的一些知识
2.2 整数表示
2.2.1 二进制表示整数
2.2.2 扩展、截断
2.3 整数运算
2.3.1 加减法与溢出
2.3.2 逆元和补码的非
2.3.3乘法
2.4浮点数
2.4.1 IEEE规则
2.4.2例图
2.1 数据存储
2.1.1 进制
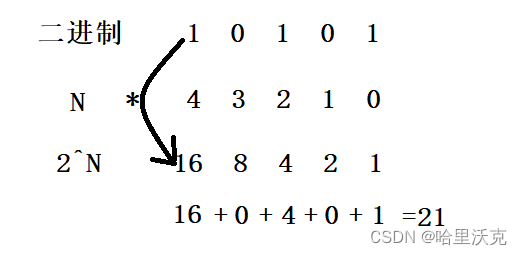
计算机中使用的进制无非涉及:二进制、十进制、十六进制
相互转换内容不做介绍,以下图片可以清晰表示
需要解释一下:上面图片的数都是符号表示的,其实他们对我们脑海里理解的那个数是一一对应的,这样就能理解了为什么要对这些数换来换去了。
2.1.2 数据在内存的存储方式---大小端
大端:高地址存储低位数据
小端:低地址存储低位数据
2.1.3 C语言的一些知识
32位:虚拟地址中,一块空间32位用来存储一个数据
64位:虚拟地址中,一块空间64位用来存储一个数据
注意:这里的32位和64位是针对计算机
而程序在生成可执行文件时,会出现32位或者64位的版本,这些程序的位是由编译的人觉得的。用64位的机器对32位64位程序都可以执行,而32位机器对64位文件不可执行。
数据基本类型:
二进制运算:
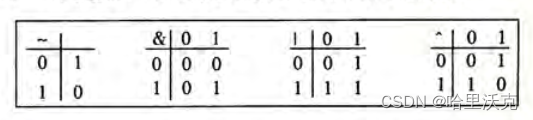
位运算:
对于右移:如果数据是无符号则是逻辑右移,有符号则是算数左移
逻辑判断:
!:非
&&:并且
||:或者
2.2 整数表示
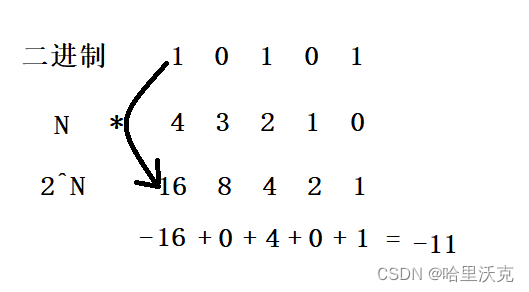
2.2.1 二进制表示整数
无符号整型:
有符号整型(补码):
最左边的一位,对于补码而言都当成负数
无符号整型与补码之间的转换
1.通常情况下,整型会被转成补码,两者再进行运算;不过可以通过强制类型转换对补码进行转换。
2.二者的转换,对于机器中的存储数据不会改变,也就是说我们不会看到机器的二进制变掉,只是解释这个数据的方式变不同了而已。
2.2.2 扩展、截断
扩展:
无符号整型的扩展:只需在其前面添加0即可
补码扩展:观察最左边的数,扩展添加的数和最左边的数一致
截断:
无论是无符号整数还是其补码,在截断时的处理都是直接截取相对于的位数,不过对于补码而言,其读取方式依旧看最前面的数是0/1。
2.3 整数运算
针对加减法,其实与十进制的运算无异
需要注意的是:
1.在计算机中,一个数据的存储位数是有限的,因此不会出现无限的数,一切都已被规定
2.不断加减可能会出现溢出现象,因为计算机的存储单元有限
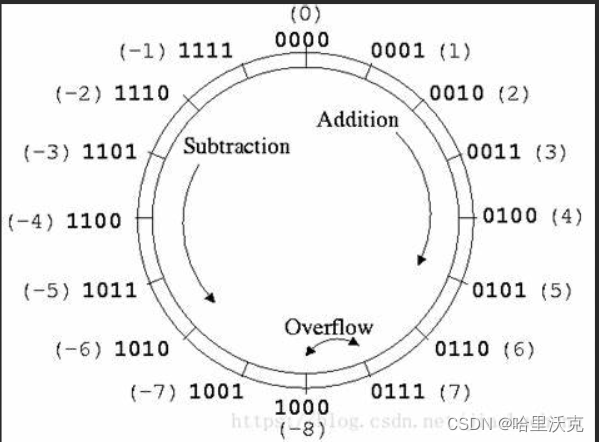
2.3.1 加减法与溢出
溢出的情况
无符号整型:相加可能溢出,溢出后的数会小于原来两个
补码:相加相减会出现正溢出和负溢出
正溢出:两个正数相加溢出;判断结果是否为负数,是则溢出
负溢出:两个负数相加溢出;判断结果是否为正数,是则溢出
2.3.2 逆元和补码的非
逆元针对无符号整数,为讨论方便我们记一个数x,其逆元为y---满足:x+y=0
不过这里说明等于0的情况有两种:
1.0+0
2.一个数加另一个数溢出得0
补码的非
情况有三种:假设存储的最小数位-8
1.(-8)+(-8)溢出为0 --- 不同的存储单元的最小数自己相加得到的就是0,故最小数的非就是自己
2.(-4)+ 4 为 0 溢出 --- 正的加负的刚好为0,意义上好理解,但是其实是溢出变成的0
3. 0+0 为0
2.3.3乘法
简单讲,就是先两个数相乘,不管如何;得到结果后,嵌入到数据的位置上。考虑位数过大要截断,最后根据是无符号还是补码确定值。
乘2的幂 --- 乘多少个2,位运算往左移几位就是结果
除2的幂 --- 除多少个2,位运算往右移几位就是结果(补码是逻辑右移)
乘一个常数其实就是计算机会优化,变成位运算多少,加减多少
2.4浮点数
2.4.1 IEEE规则
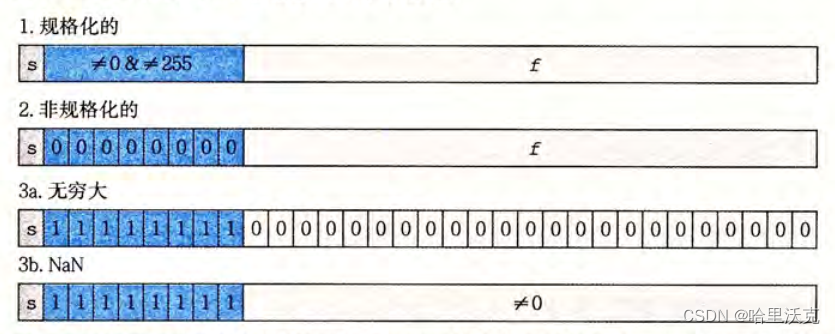
根据上面的存储形式,其实我们不难发现浮点数的表达分为三部分:
正负符号(S),阶数(E),尾数(M)
三种形式:
1.规格化
S(符号):0为正,1为负
E(阶数):exp-Bias
M(尾数):1+f中的内容
(-1)^S *(1+M)* E
2.非规格化
S(符号):0为正,1为负
E(阶数):1-Bias
M(尾数):f中的内容
(-1)^S * M * E
2.4.2例图
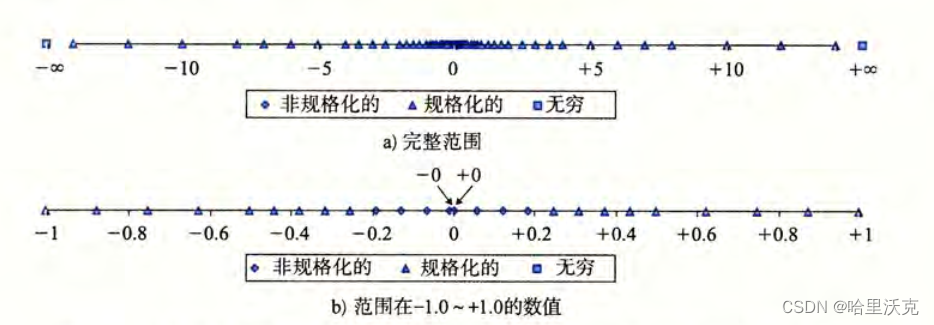
k=3,n=2 ==> 格式为 0 000 00
1.非规格范围便是k位全是0,S代表正负,f中的内容全为1得到一个比0.2小一点的数,所有我们看b图可见非规格都在-0.2~0.2之间分布
2.规格最大k位为110,f的内容也全为1,得到最大 (0/1) 110 11;在-14~14之间
3.正负无穷
4.注意,0分为+0和-0,因为非规范数的符号可以表示正负,其他位为0