文章目录
- 位图概念
- 位图操作
- 位图代码
- 位图应用
位图概念
boss直接登场:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中❓
40亿个整数,大概就是16GB。40亿个字节大概就是4GB。
1Byte=8bit
1KB=1024Byte
1MB=1024KB=1024*1024=1048576字节
1GB=1024MB=1024*1048576≈10亿字节,所以4GB约等于40亿字节
1TB=1024GB
如果采用排序+二分的做法来查找:排序要用到数组,要开出16GB大的数组,排在数组里才能进行二分查找,但是这些数组在内存里放不下,所以排序都排不了。那只能放到磁盘上,那数据在磁盘上就不能用二分了,不支持下标,效率也慢。
如果用红黑树和哈希表:数组都存放不下,红黑树和哈希表更不用说了,红黑树三叉链结构+颜色,消耗更大,哈希表也有消耗:存放_next指针,负载因子等问题,内存放不下。
下面,我们解决这个问题的方法是位图
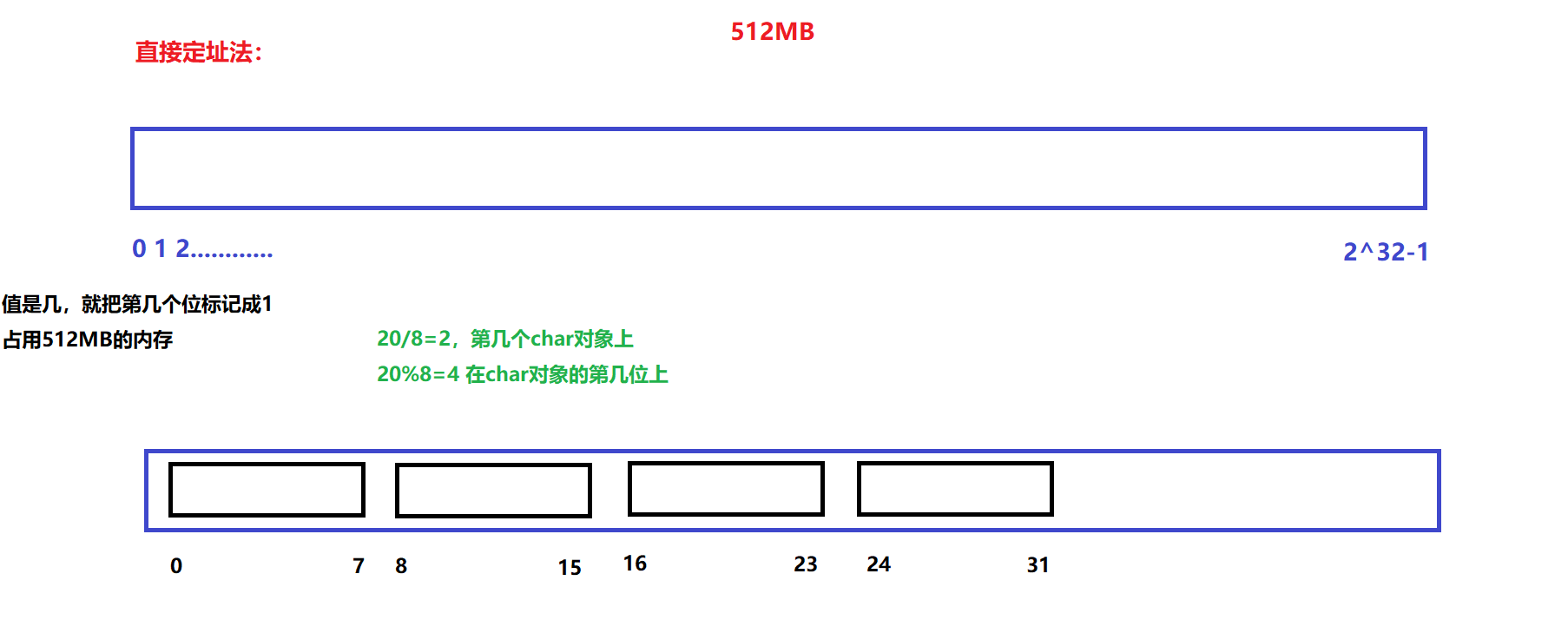
这个问题是在不在的问题,是key的模型,那我们可以标记在还是不在,我们只需要一个比特位就可以标记在还是不在
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。
位图概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的
位图操作
位图核心的三个操作是set、reset和test。
set是将x对应的比特位置设为1,reset是将x对应的比特位置设为0,test用来查看x在不在
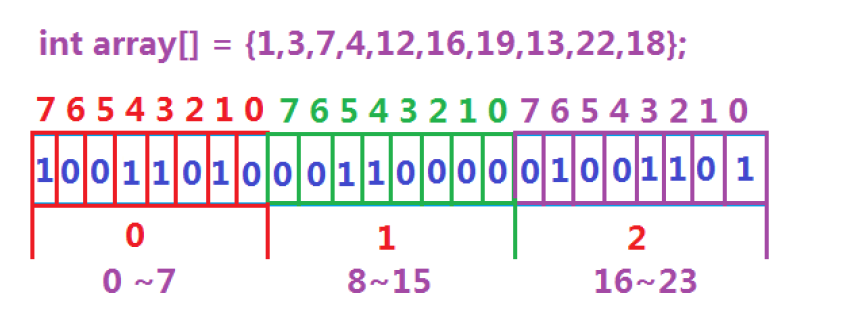
set将对应的比特位置设为1:_bits[i]|=(1<<j)
reset将对应的比特位置设为0:_bits[i]&=(~(1<<j))
test查看x在或不在:_bits[i]&(1<<j)
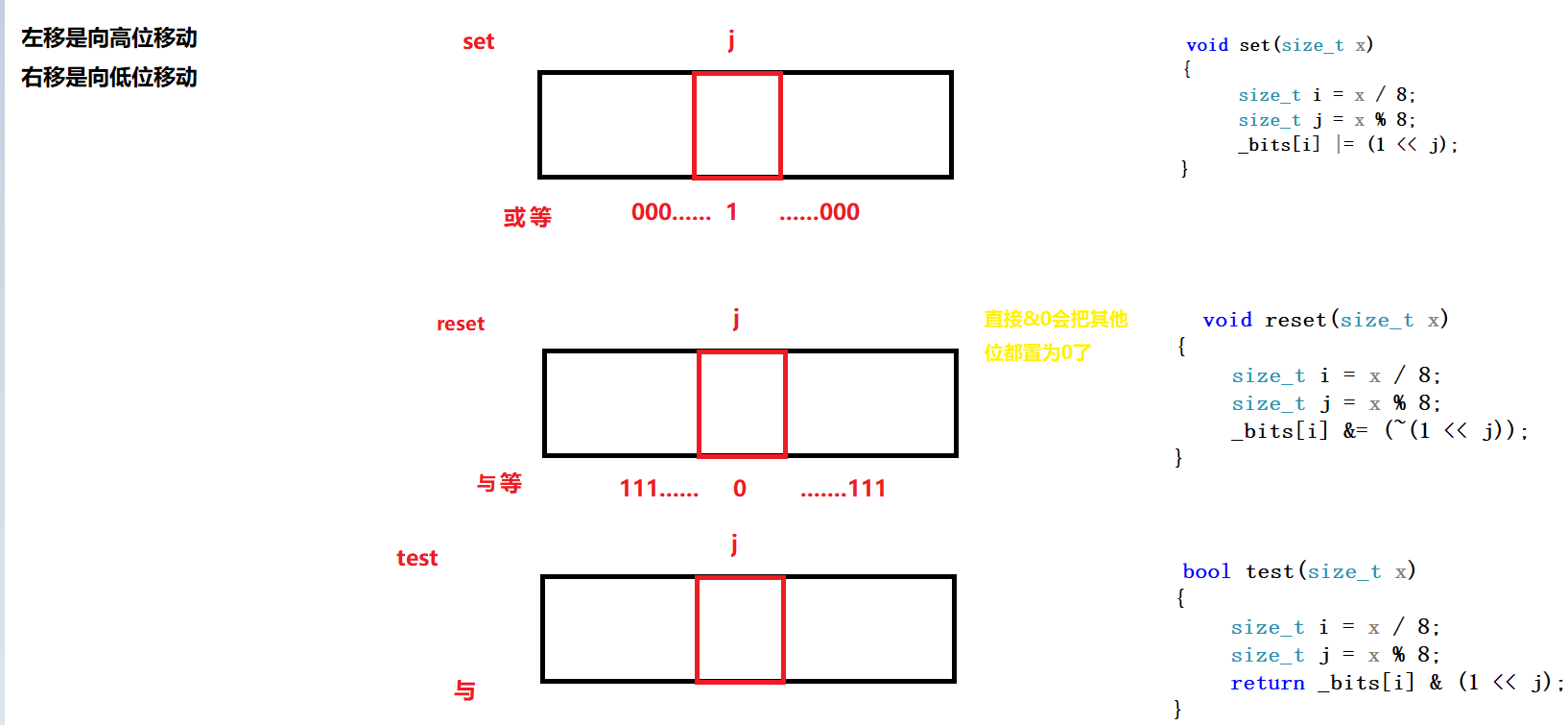
void set(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
_bits[i] |= (1 << j);
}
void reset(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
_bits[i] &= (~(1 << j));
}
bool test(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
return _bits[i] & (1 << j);
}
位图代码
#pragma once
#include <iostream>
#include <vector>
using namespace std;
namespace hwc
{
template<size_t N>
class bitset
{
public:
bitset()
{
_bits.resize(N/8+1, 0);
}
void set(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
_bits[i] |= (1 << j);
}
void reset(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
_bits[i] &= (~(1 << j));
}
bool test(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
return _bits[i] & (1 << j);
}
private:
vector<char> _bits;
};
void test_bitset()
{
//bitset<100> bs1;
//bitset<-1> bs2;//
bitset<0xffffffff> bs2;
bs2.set(10);
bs2.set(20);
bs2.set(3000);
cout << bs2.test(10) << endl;
cout << bs2.test(20) << endl;
cout << bs2.test(3000) << endl;
cout << bs2.test(666) << endl;
cout << bs2.test(777) << endl << endl;
bs2.reset(20);
bs2.set(666);
cout << bs2.test(10) << endl;
cout << bs2.test(20) << endl;
cout << bs2.test(3000) << endl;
cout << bs2.test(666) << endl;
cout << bs2.test(777) << endl;
}
}
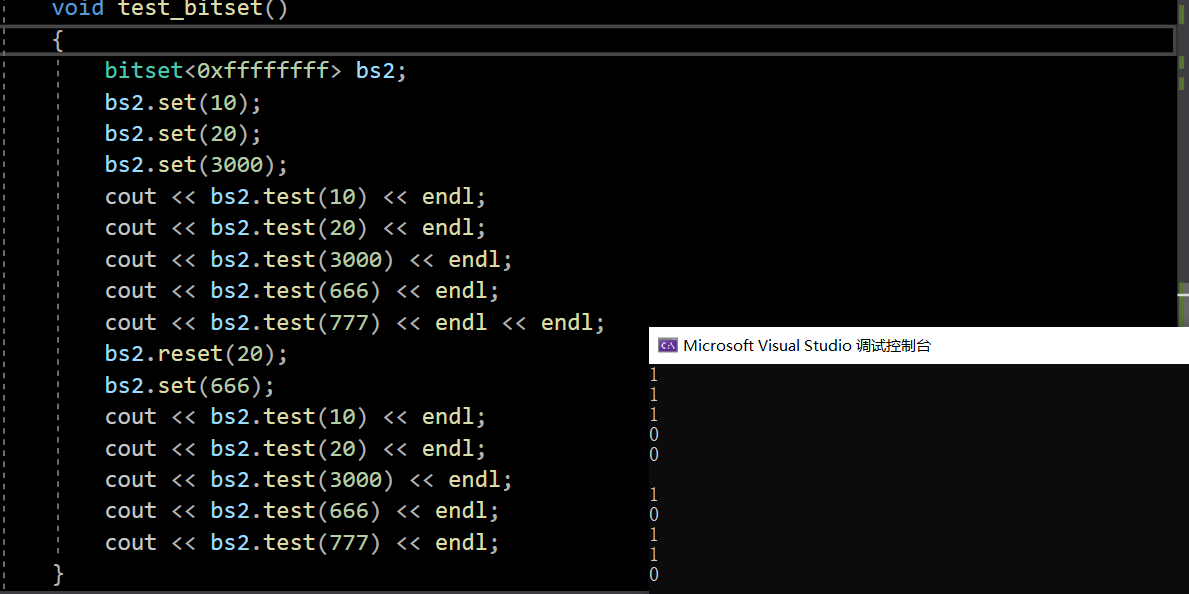
小细节:(-1)的size_t类型
实际上,库里面也有位图:
位图应用
\1. 快速查找某个数据是否在一个集合中
\2. 排序
\3. 求两个集合的交集、并集等
\4. 操作系统中磁盘块标记
给定 100 亿个整数,设计算法找到只出现一次的整数
100亿个数字找到只出现一次的整数,这是KV模型的统计次数,数字有三种状态:0次、1次、1次以上,。这三种状态需要用两个比特位就可以表示,分别位00代表0次,01代表1次,10代表1次以上既可以。我们可以采用两个位图来实现,复用上面所实现的位图即可解决问题
template<size_t N>
class twobitset
{
public:
void set(size_t x)
{
if (!_bs1.test(x) && !_bs2.test(x))//00
{
_bs2.set(x);//01
}
else if (!_bs1.test(x) && _bs2.test(x))//01
{
_bs1.set(x);
_bs2.reset(x);//10
}
//10不变
}
void PrintOnce()
{
for (size_t i = 0; i < N; ++i)
{
if (!_bs1.test(i) && _bs2.test(i))
{
cout << i << endl;
}
}
cout << endl;
}
private:
bitset<N> _bs1;
bitset<N> _bs2;
};
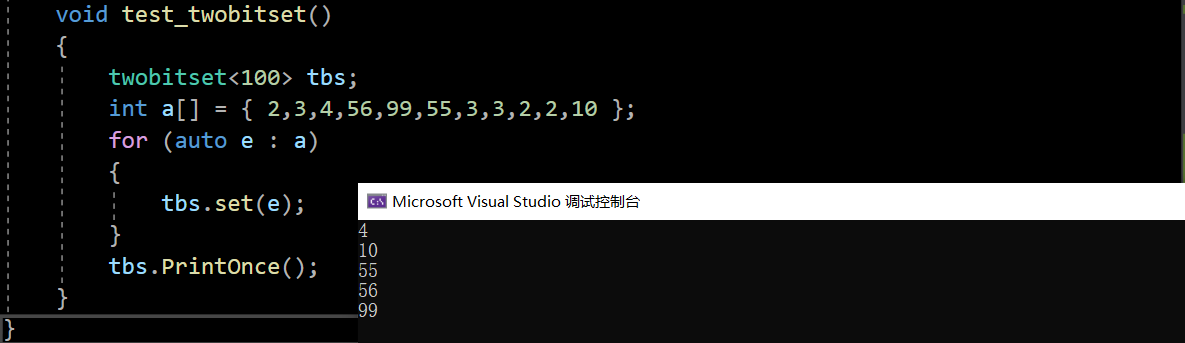
void test_twobitset()
{
twobitset<100> tbs;
int a[] = { 2,3,4,56,99,55,3,3,2,2,10 };
for (auto e : a)
{
tbs.set(e);
}
tbs.PrintOnce();
}
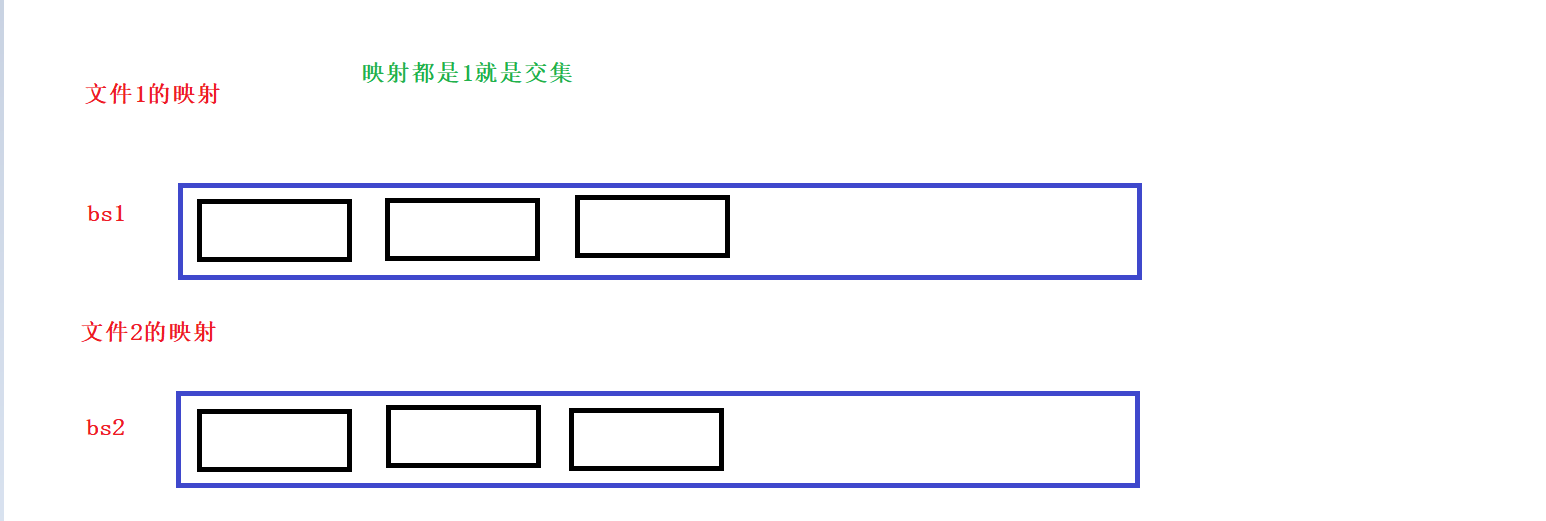
给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
1 个文件有 100 亿个 int,1G内存,设计算法找到出现次数不超过2次的所有整数
这与上面的类似,多判断一次
把10->11,最后找不超过两次的整数
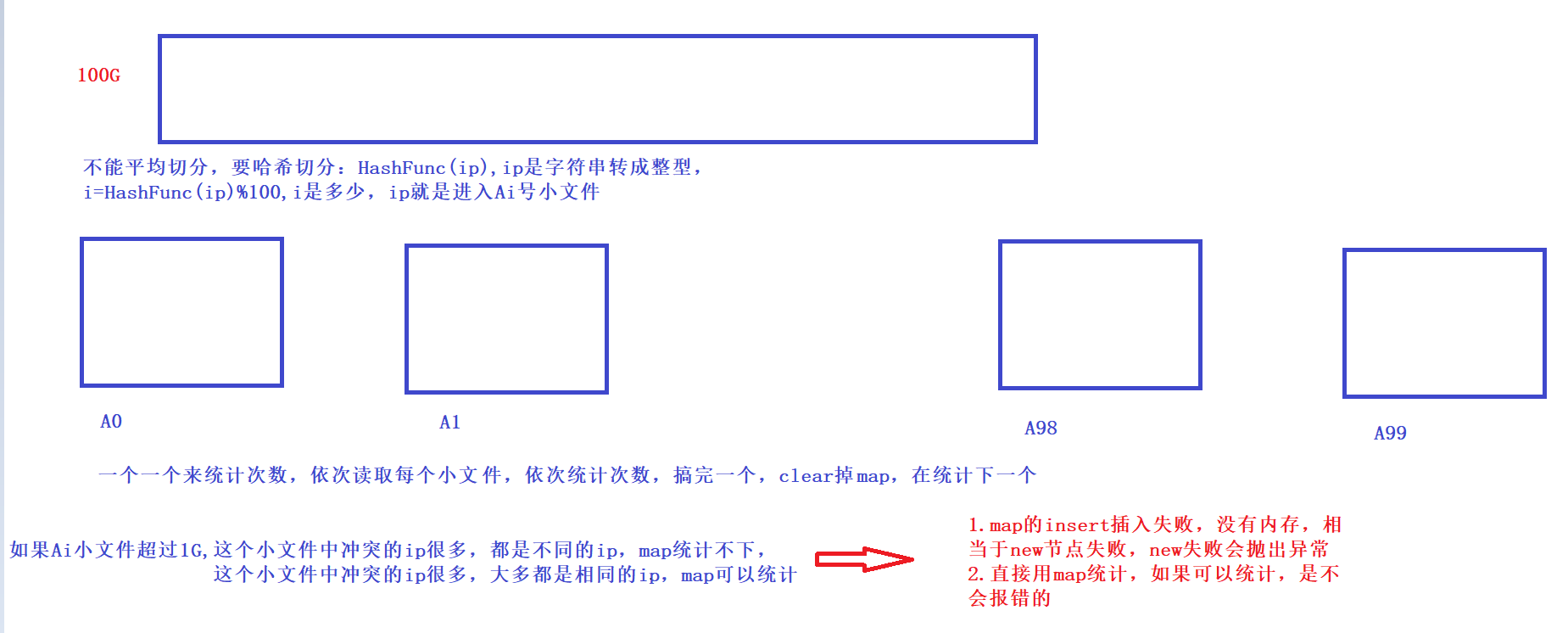
给一个超过100G大小的log file,log中存着IP地址,设计算法找到出现次数最多的IP地址
统计次数自然是要map的,map有附带消耗,三叉链。位图只能判断在不在。所以还是要用map统计的:
我们可以把整个文件通过哈希切分成小的文件,然后去进行统计次数,但是如果小的文件超过1G,说明了这个小文件有两种情况:
1.这个小文件冲突的ip很多,但都是不同的ip,map统计不下------->map的insert插入失败,没有内存,相当于new节点失败,new失败会抛出异常
2.这个肖文杰冲突的ip很多,大多都是相同的ip,map可以统计-------->直接用map统计,可以统计,不会报错
位图特点:位图只能处理整形。采用位图标记字符串时,必须先将字符串转化为整形的数字,找到位图对应的比特位置