题目描述
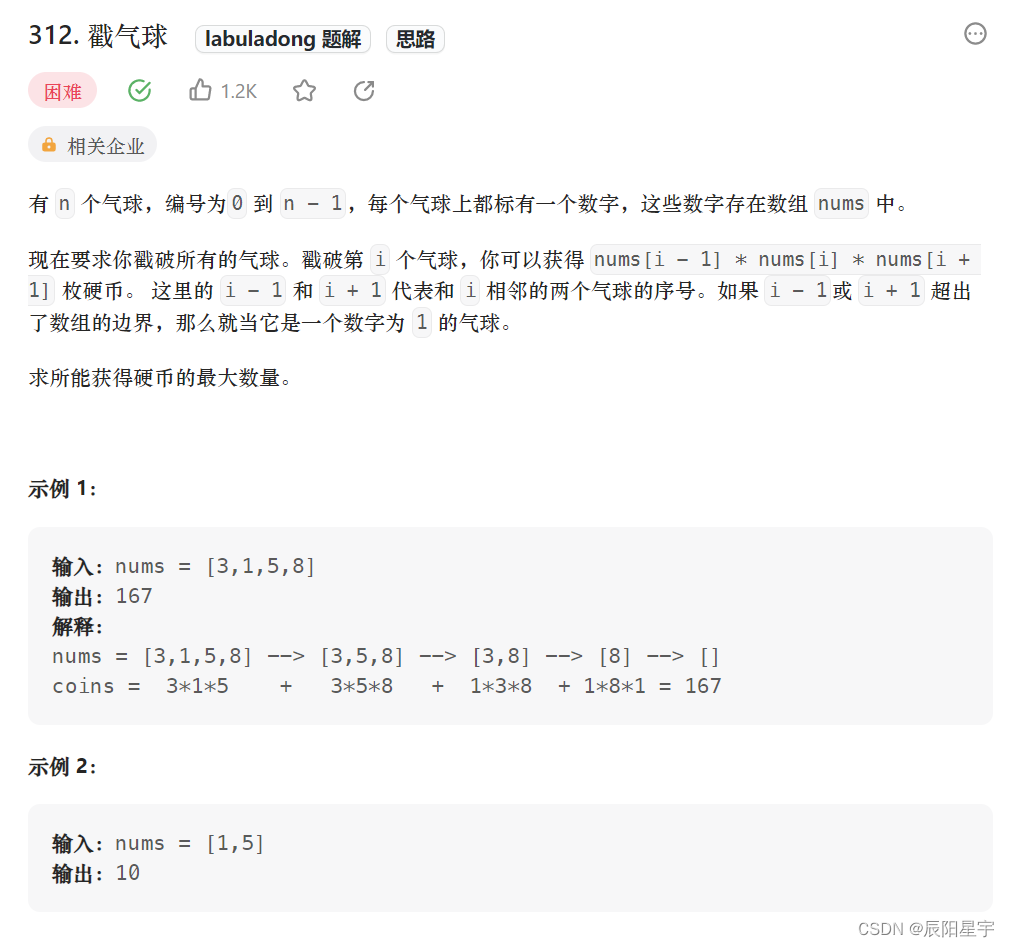

原题链接:312. 戳气球
解题思路
(1)回溯法
很多求最值实际上就是穷举所有情况,对比找出最值。因为不同的戳气球顺序会产生不一样的结果,所以实际上这就是一个全排列问题。
class Solution {
public:
int res = 0;
void backtracking(vector<int>& nums, int ballonNum, int score) {
// 全戳完后找最大方案
if(ballonNum == 0) {
res = max(res, score);
}
for(int i = 0; i < nums.size(); i++) {
// 获取分数
int point = nums[i];
if(i - 1 >= 0) point *= nums[i - 1];
if(i + 1 < nums.size()) point *= nums[i + 1];
// 移除此位置
int temp = nums[i];
nums.erase(nums.begin() + i);
// 向下探查
backtracking(nums, ballonNum - 1, score + point);
// 回溯恢复
nums.insert(nums.begin() + i, temp);
}
}
int maxCoins(vector<int>& nums) {
backtracking(nums, nums.size(), 0);
return res;
}
};
此方式会超时
(2)动态规划
此题和其他动态规划题的一个区别就是,i、i+1、i-1相互有关,而动态规划算法使用的一个重要条件就是子问题需要相互独立。因此,为了可以使用动态规划,需要巧妙地定义dp数组,避免子问题产生相关性。因为,戳到最后时,也会左右乘上1,因此我们让nums的前后都加上1。
- 动态规划五部曲:
(1)dp[i][j]含义:
在i - 1到j - 1中可得到的最大硬币数(因为首尾新增了两个数,因此不戳首尾按开区间算)。
(2)递推公式:
我们如果正向思考的话就是回溯算法那种形式,那么我们再换一种方式,逆向思考计算戳的是最后一个气球时,得到的金币数量,此时递推公式就变为:dp[i]][j] = nums[i] * nums[k] * nums[j] + dp[i][k] + dp[k][j],其中(i < k < j)为开区间。
(3)dp数组初始化:
dp[0][0] = dp[0][1] = 0,因为最少需由三个数组成,因此i=0,j=0,1时都为非法形式,初始化为0即可。
(4)遍历顺序:
从下到上,从左到右。每次求到k时,需要i-k和k-j的信息,因此从下到上,可以保证有k-j的信息,从左到右可以保证有i-k的信息。
(5)举例: (省略)
class Solution {
public:
int maxCoins(vector<int>& nums) {
// 首尾添加1
nums.insert(nums.begin(), 1);
nums.push_back(1);
int n = nums.size();
vector<vector<int>> dp(n, vector<int>(n, 0));
// 从n-2开始,相当于从原nums数组中的最后一个位置开始
for(int i = n - 2; i >= 0; i--) {
// 从i+2开始,留出i+1给k
for(int j = i + 2; j <= n - 1; j++) {
// k在i和j中尝试
for(int k = i + 1; k < j; k++) {
dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] + \
nums[i] * nums[k] * nums[j]);
}
}
}
return dp[0][n - 1];
}
};
参考文章:动态规划套路解决戳气球问题、戳气球