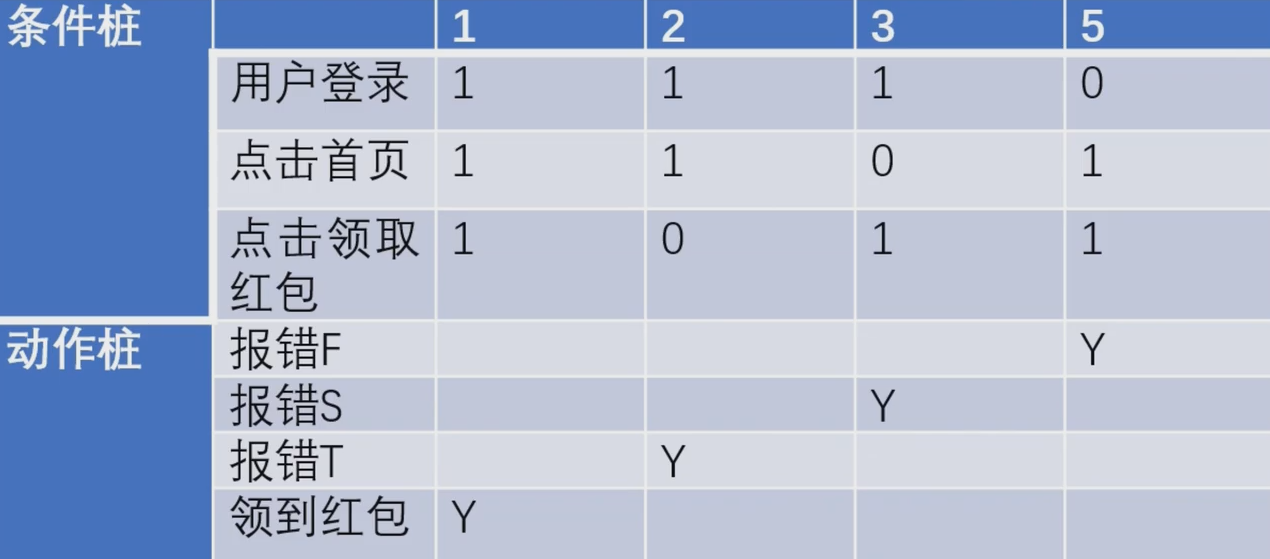
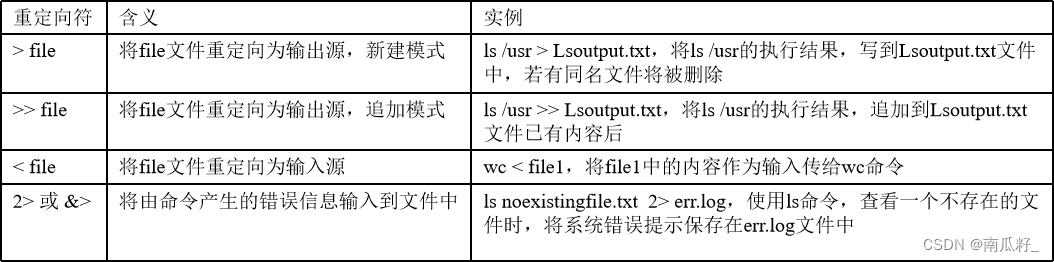
文章目录
- 膨胀卷积
- 为什么需要膨胀卷积
- gridding effect
- 连续使用三次膨胀卷积——1
- 连续使用三次膨胀卷积——2
- 连续使用三次膨胀卷积——3
- Understanding Convolution for Semantic Segmentation
膨胀卷积
膨胀卷积,又叫空洞卷积。

左边是普通卷积,右边是膨胀卷积。
r 表示间隙,即膨胀因子。(当 r = 1时就是普通卷积)
一般使用过程中, 输入和输出特征图的高和宽是不会发生变化的。
复习:N = (W - F + 2P)/ S + 1
为什么需要膨胀卷积
在语义分割任务中,通常会使用分类网络作为backbone,在backbone中会对图片进行一系列的下采样。通过backbone之后,会使用一系列的上采样恢复原来的图片大小。如果特征图的高宽下采样倍率太大的话,还原到原来尺寸后,图片将丢失很多细节信息。
例如,在VGG网络中,通过max pooling层进行池化,这降低了特征图的高度和宽度,也丢失了一些细节信息,而丢失的信息无法通过上采样进行还原,在语义分割任务中将导致分割的效果不理想。而如果去掉max pooling层,将导致特征图的感受野变小。
利用膨胀卷积,既能增大感受野,又能保持输入输出特征图的高和宽不发生变化,解决了上述问题。但是,是否无脑堆叠膨胀卷积就可以了呢?
参考论文Understanding Convolution for Semantic Segmentation,在膨胀卷积使用过程中,会出现gridding effect的问题。
gridding effect
首先了解 什么是 gridding effect 问题:
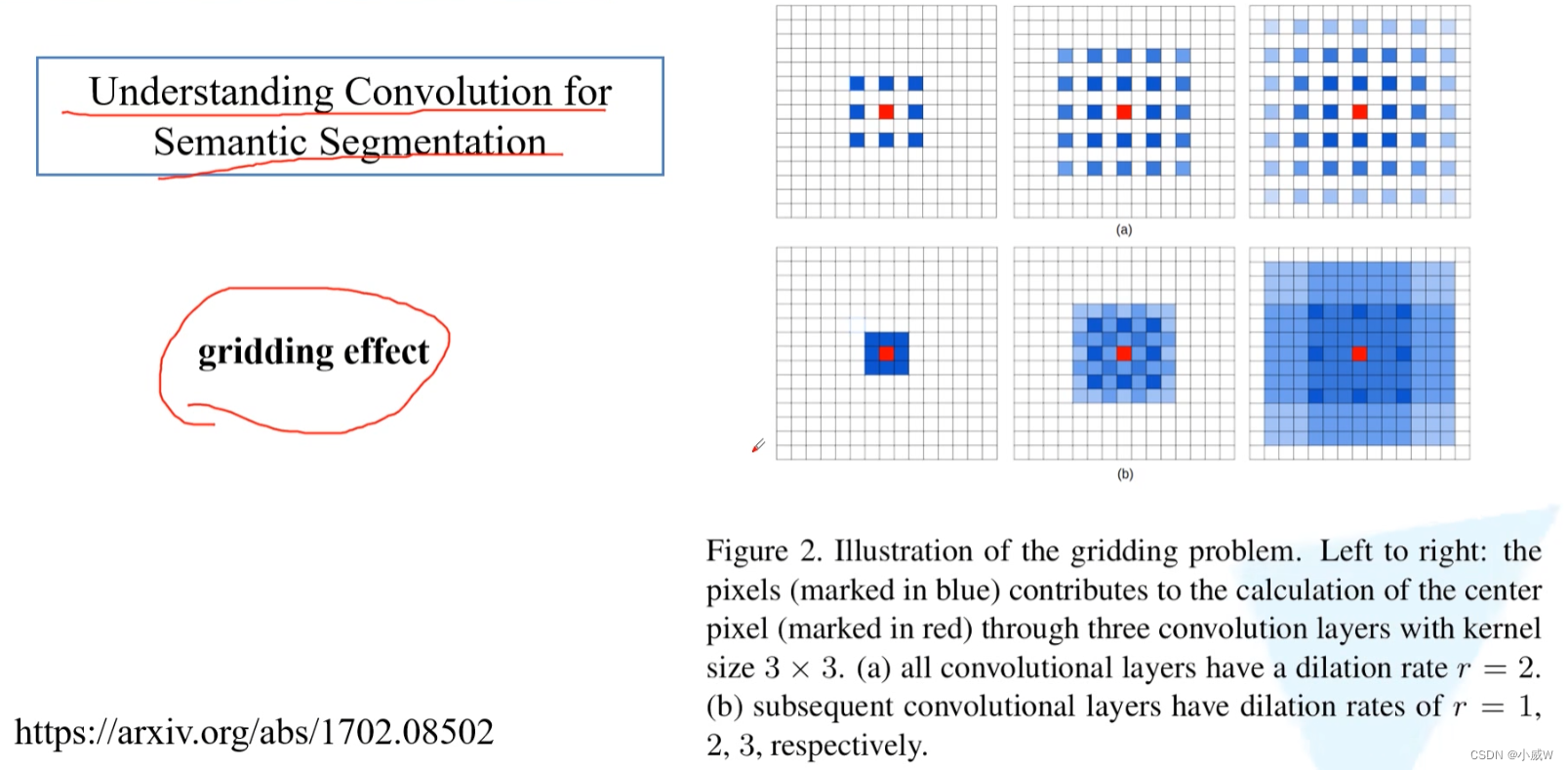
连续使用三次膨胀卷积——1
layer4上中心点使用各个点的信息的次数:
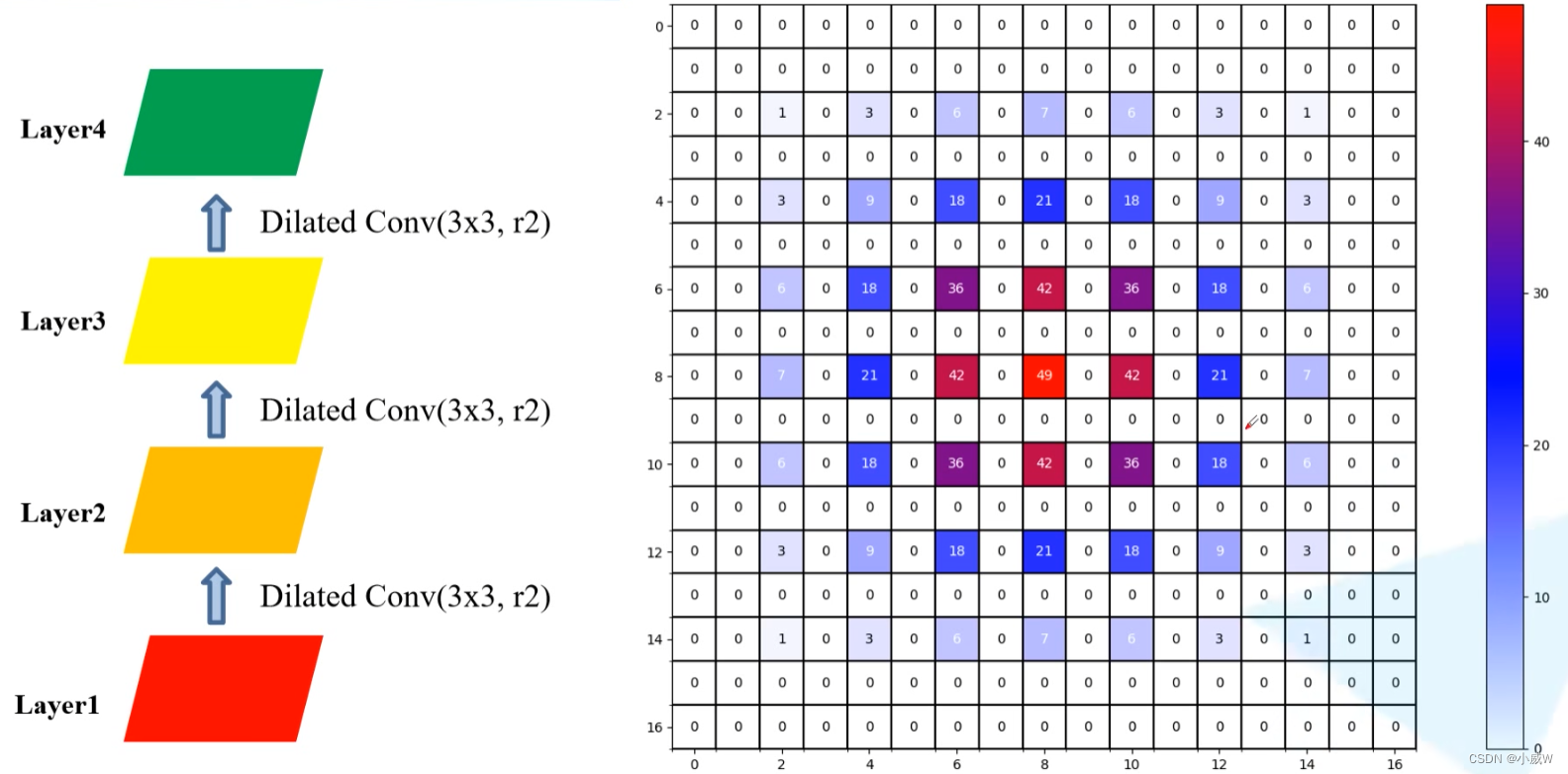
这就是gridding effect现象,即layer4上的一个像素并没有利用到这个范围内所有像素点的信息,而是有间隔的。(这就会导致一些细节上信息的丢失)。
连续使用三次膨胀卷积——2
与实验一不同的是,第一个膨胀卷积的膨胀因子为1,也就是普通卷积。
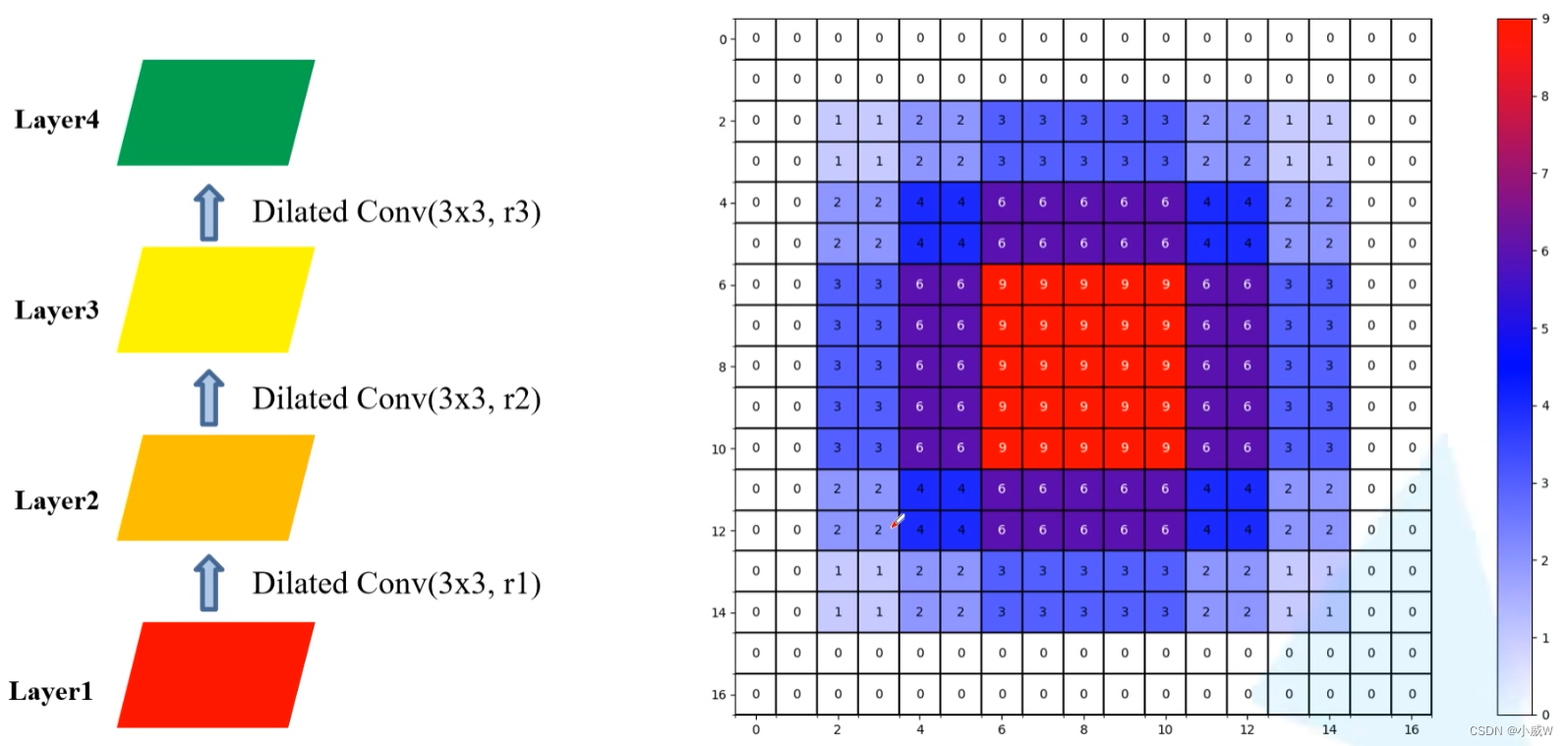
这里一个像素点使用的信息已经是某个范围内全部像素点的信息了。
感受野(RF,receptive field)= 13 × 13
连续使用三次膨胀卷积——3
连续使用三个普通卷积。
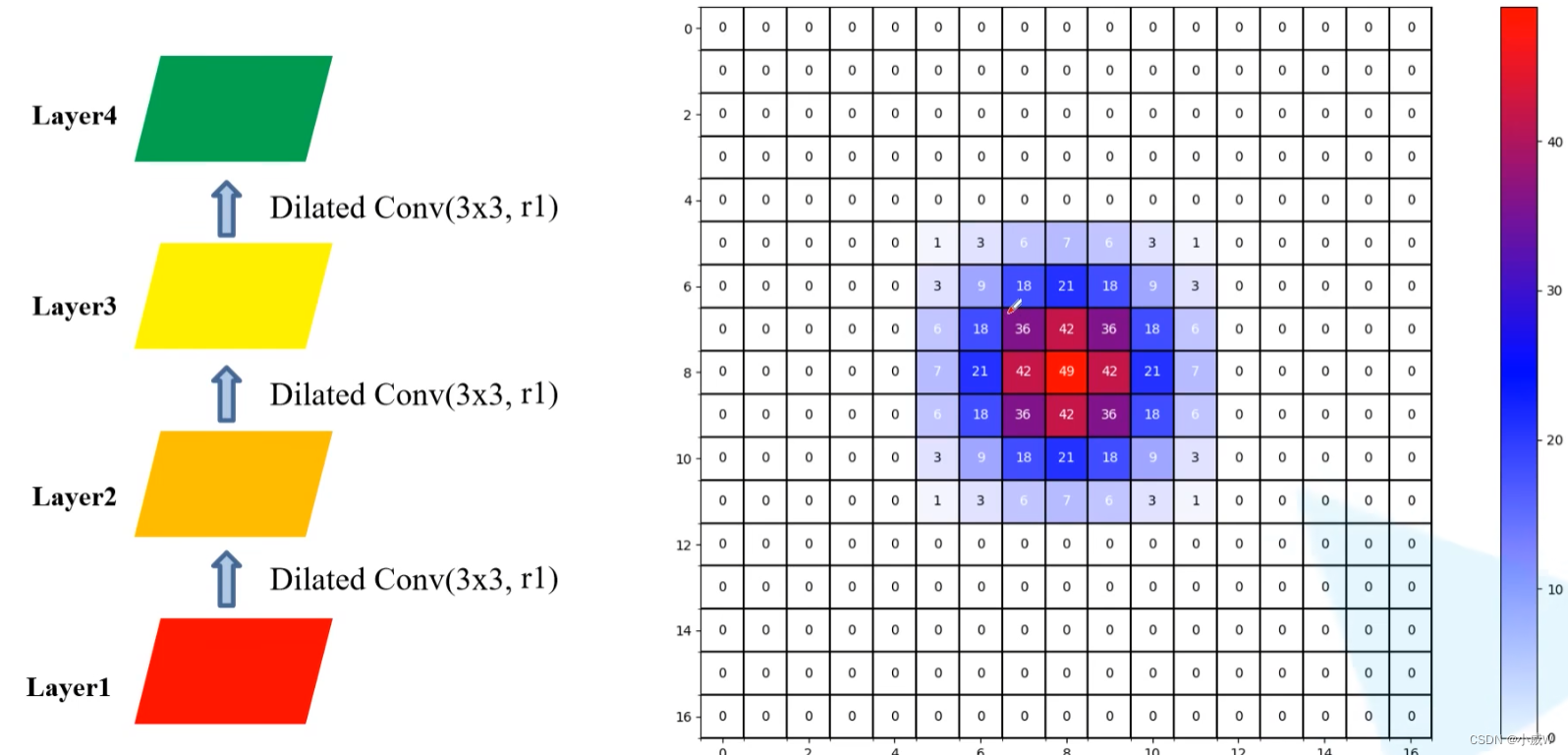
感受野(RF,receptive field)= 7 × 7
实验 2 和 3 对比,可以发现使用膨胀卷积在参数数量相同的情况下可以使感受野变大很多。
Understanding Convolution for Semantic Segmentation
@article{PanquWang2018UnderstandingCF, title={Understanding Convolution for Semantic Segmentation}, author={Panqu Wang and Pengfei Chen and Ye Yuan and Ding Liu and Zehua Huang and Xiaodi Hou and Garrison W. Cottrell}, journal={Workshop on Applications of Computer Vision}, year={2018}}
https://readpaper.com/paper/2592939477

Mi 表示第 i 层两个非零元素(即被使用到的像素)之间的最大距离。
设计原则1:需要 M2 <= K。
[1,2,5]
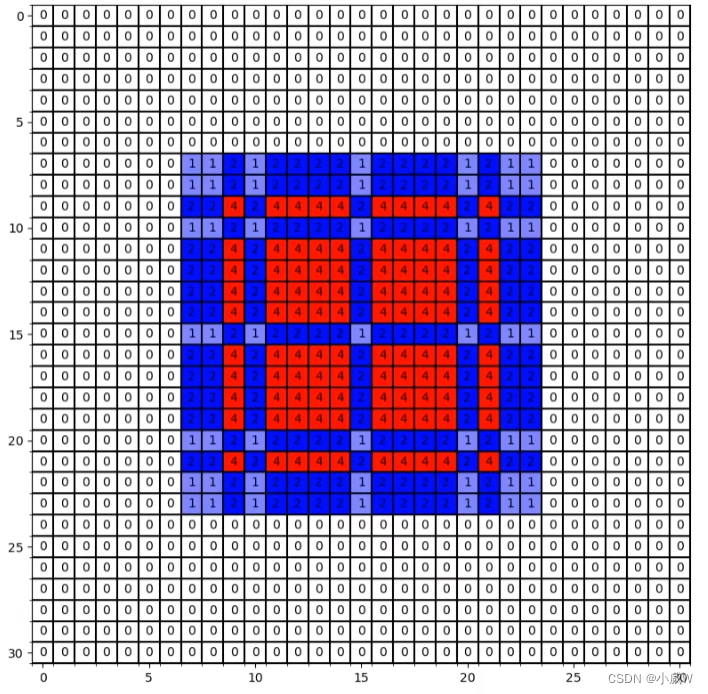
[1,2,9]
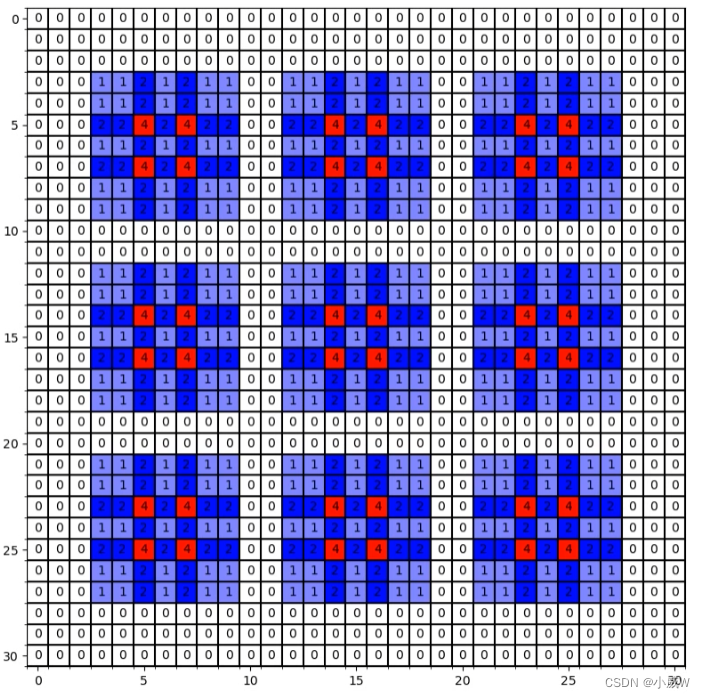

设计原则2:锯齿状膨胀因子设置,如[1,2,3,1,2,3]

设计原则3:公约数不能大于1
[2,4,8]
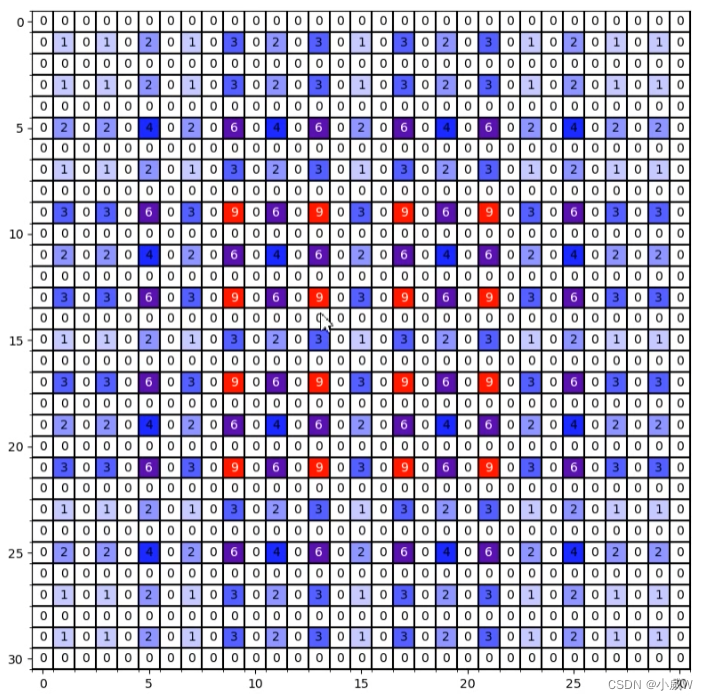
结果对比:
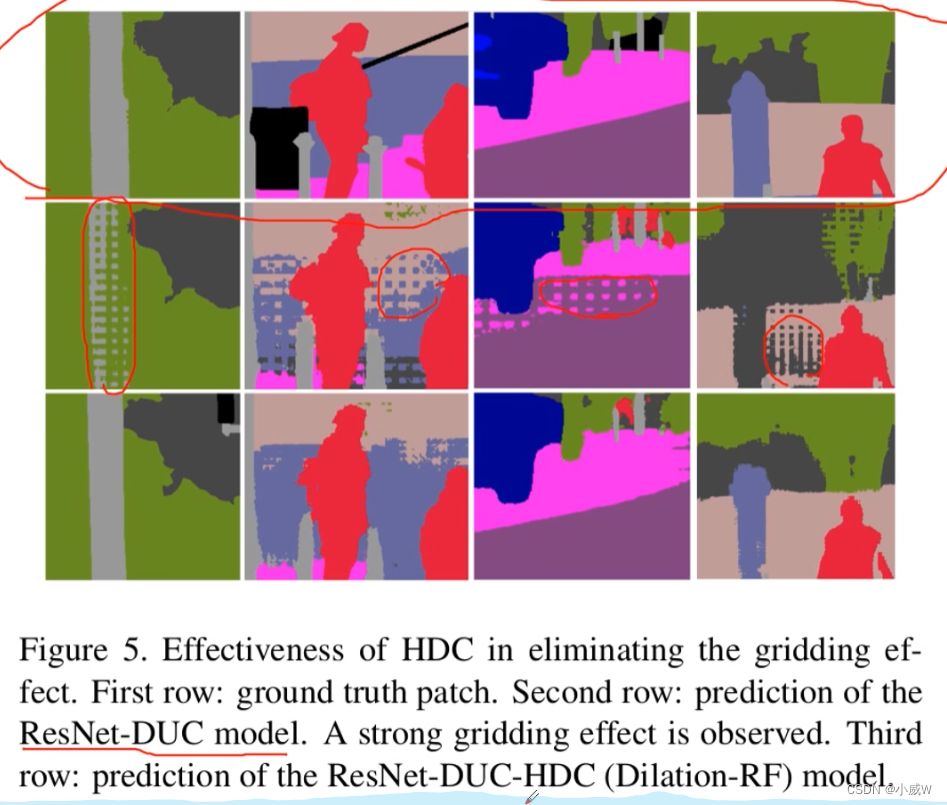
参考资料:
https://blog.csdn.net/Zen_of_code/article/details/127536998
https://www.bilibili.com/video/BV1Bf4y1g7j8/