1 子序列与上升子序列

1.1 子序列

一个序列A={a1,a2,...an}中任意删除若干项，剩余的序列叫做A的一个子序列。例如序列A={1,3,5,4,2}，删除其中的第3项和第5项，得到序列B={1,3,4}，删除其中的第3项和第4项，得到序列C={1，3，2}，此时序列B和C是序列A的子序列。

1.2 上升子序列

如果序列中的元素是从小到大排列的，则该序列为上升序列，如果该序列又是其它序列的子序列，则称为上升子序列。例如“1.1 子序列”中提到的B是A的上升子序列，而C是A的子序列，但不是上升子序列。

1.3 最长上升子序列

包含元素最多的上升子序列，叫做最长上升子序列。例如，序列D={1,5}，是序列A的上升子序列，但不是最长上升子序列，而序列B是A的最长上升子序列。

2 动态规划求解最长上升子序列

2.1 流程

求解一个序列的最长上升子序列问题的流程如图1所示：

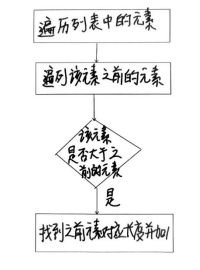
图1 求解最长上升子序列流程

从图1中可以看出，在遍历素组中的元素时，如果该元素的值大于该元素之前的元素值时，就有可能构成上升子序列，此时需要找到之前元素对应的最长子序列的长度，找到这些长度的最大值，并且对该最大值加1，即为当前元素对应的最长子序列。从以上分析可知，动态规划求解最长上升子序列的“状态转移方程”为

dp(n) = max(dp(1),dp(2),...dp(n-1))+1

其中，n表示数组中元素的位置，即索引值。

2.2 核心代码

序列的最长上升子序列的核心代码如下所示：

for (int i = 1; i <= n; i++)
{
	dp[i] = 1;
	for (int j = 1; j <= i - 1; j++)
	{
		if (a[i] > a[j])
		{
			dp[i] = max(dp[i], dp[j]+1);
		}
	}
	length = max(length, dp[i]);
}

其中，第一个循环表示遍历数组中的所有元素；第二个循环表示遍历该元素之前的所有元素；第8行代码为“状态转移方程”；第11行代码的作用是找到数组中所有元素对应的最大值，即最长上升子序列的长度。

2.3 完整代码

序列的最长上升子序列的完整代码如下所示：

#include <iostream>
using namespace std;
 
int main()
{
	int a[10001] = { 0 };
	int dp[10001] = { 0 };
	int n;
	int length = 0;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
 
	for (int i = 1; i <= n; i++)
	{
		dp[i] = 1;
		for (int j = 1; j <= i - 1; j++)
		{
			if (a[i] > a[j])
			{
				dp[i] = max(dp[i], dp[j]+1);
			}
		}
		length = max(length, dp[i]);
	}
	cout<<(length);
	return 0;
}