注意事项:
本题dp思路与 “线性dp–方格取数” 一致,下方思路仅证明为什么使用方格取数的思路是正确的。
题目:
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。
一次素质拓展活动中,班上同学安排坐成一个 m
行 n 列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。
幸运的是,他们可以通过传纸条来进行交流。
纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标 (1,1),小轩坐在矩阵的右下角,坐标 (m,n)。
从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。
班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙,反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用 0表示),可以用一个 0∼100的自然数来表示,数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。
现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有 2个用空格隔开的整数 m和 n,表示学生矩阵有 m行n列。
接下来的 m行是一个 m×n的矩阵,矩阵中第 i行 j列的整数表示坐在第 i行 j列的学生的好心程度,每行的 n个整数之间用空格隔开。
输出格式
输出一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
数据范围
1≤n,m≤50
输入:
3 3
0 3 9
2 8 5
5 7 0
输出:
34
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55;
int w[N][N], f[N+N][N][N]; //注意k要开两倍,因为是i+j的总和
int n, m;
int main()
{
cin >> n >> m;
n = max(n, m); //这里n使用较大的做为边界即可,因为多算几个0不影响结果
for (int i = 1; i<=n; i++)
for (int j = 1; j<=m; j++) cin >> w[i][j];
//线性dp
for (int k = 2; k<=n+m; k++) {
for (int i1 = 1; i1<=n; i1++) {
for (int i2 = 1; i2<=n; i2++) {
// k = i1+j1 = i2+j2, 切记是相等关系
int j1 = k-i1, j2 = k-i2;
if (j1>=1 && j2>=1 && j1<=n && j2<=n) { //判断j1和j2的合法性
//如果是重叠点就只加一次,例如(1,2)(1,2), 如果是非重叠点就将两个点都加上,例如(1, 2)(2, 1)
int t = w[i1][j1];
if (i1 != i2) t += w[i2][j2];
//引用节省代码量,分四种情况讨论上两个点如何进行移动
int &x = f[k][i1][i2];
x = max(x, f[k-1][i1-1][i2-1]); //down,down
x = max(x, f[k-1][i1-1][i2]); //down,right
x = max(x, f[k-1][i1][i2-1]); //right,down
x = max(x, f[k-1][i1][i2]); //right, right
x += t;
}
}
}
}
cout << f[n+m][n][n];
return 0;
}
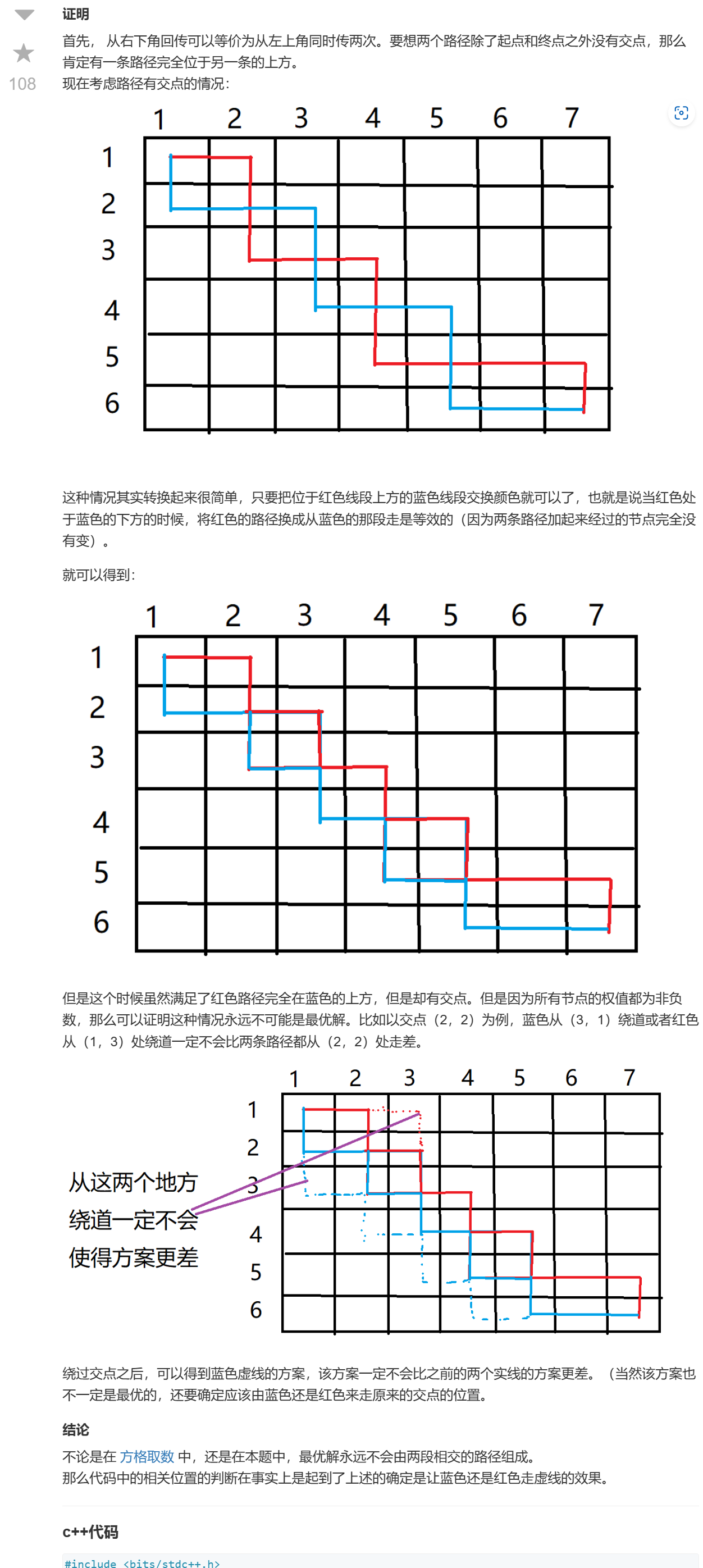
思路:
这里直接贴vlehr大佬的画图解释(原链接):
已经讲的非常清晰了,自认讲不明白,就借用下大佬的吧哎嘿~
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流



![[Java·算法·中等]LeetCode215. 数组中的第K个最大元素](https://img-blog.csdnimg.cn/79935be653c64a66a673a381996da929.png)