👉️ 力扣原文

题目

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例

输入: [3,2,1,5,6,4], k = 2
输出: 5

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

分析思路1

使用优先队列堆排序（效率太差）

题解1

class Solution {
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> heap = new PriorityQueue<>((n1,n2)->n1-n2);
        for (int n : nums){
            heap.add(n);
        }
        while (heap.size() > k){
            heap.poll();
        }
        return heap.poll();
    }
}

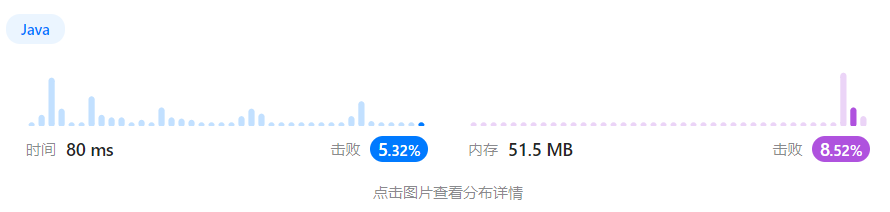
执行结果

分析思路2

借助Array工具类排序，然后取[数字长度-k]位元素。

题解2

class Solution {
    public int findKthLargest(int[] nums, int k) {
        Arrays.sort(nums);
        int n = nums.length;
        return nums[n-k];
    }
}

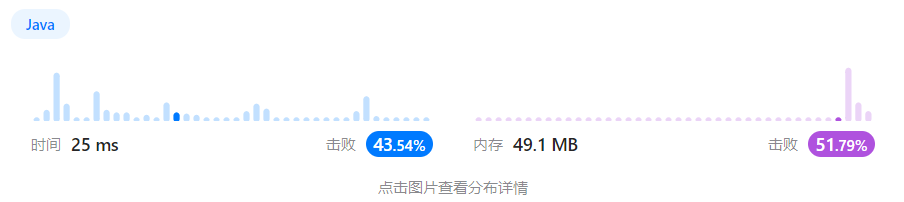
执行结果

分析思路3

采用了快速排序中的分区思想，即将一个数组分成小于某个元素和大于某个元素两部分。可以使用左右指针法进行查找。

在每次分区的过程中，通过比较当前元素与分界点的大小关系，将其移到左右两部分中。然后，对左右两部分进行递归，直到找到第N-K+1小的元素时返回结果。

题解3

public class Solution {

    /**
     * 找到数组中第K个最大元素
     * 
     * @param nums 数组
     * @param k    第K个
     * @return 第K个最大元素
     */
    public int findKthLargest(int[] nums, int k) {
        // 转化为第N-K+1小的元素
        int target = nums.length - k;

        int left = 0;
        int right = nums.length - 1;

        // 左右指针法查找第N-K+1小的元素
        while (left < right) {
            int pivotIndex = partition(nums, left, right);
            if (pivotIndex == target) {
                return nums[pivotIndex];
            } else if (pivotIndex < target) {
                left = pivotIndex + 1;
            } else {
                right = pivotIndex - 1;
            }
        }

        return nums[left];
    }

    /**
     * 分区，返回分区点的下标
     * 
     * @param nums  数组
     * @param left  左下标
     * @param right 右下标
     * @return 分区点的下标
     */
    private int partition(int[] nums, int left, int right) {
        int pivot = nums[right];
        int i = left - 1;

        for (int j = left; j < right; j++) {
            if (nums[j] <= pivot) {
                i++;
                swap(nums, i, j);
            }
        }

        swap(nums, i + 1, right);

        return i + 1;
    }

    /**
     * 交换数组中两个元素的位置
     * 
     * @param nums 数组
     * @param i    位置i
     * @param j    位置j
     */
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

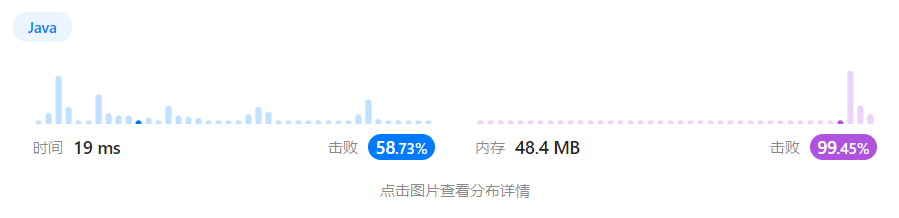
执行结果