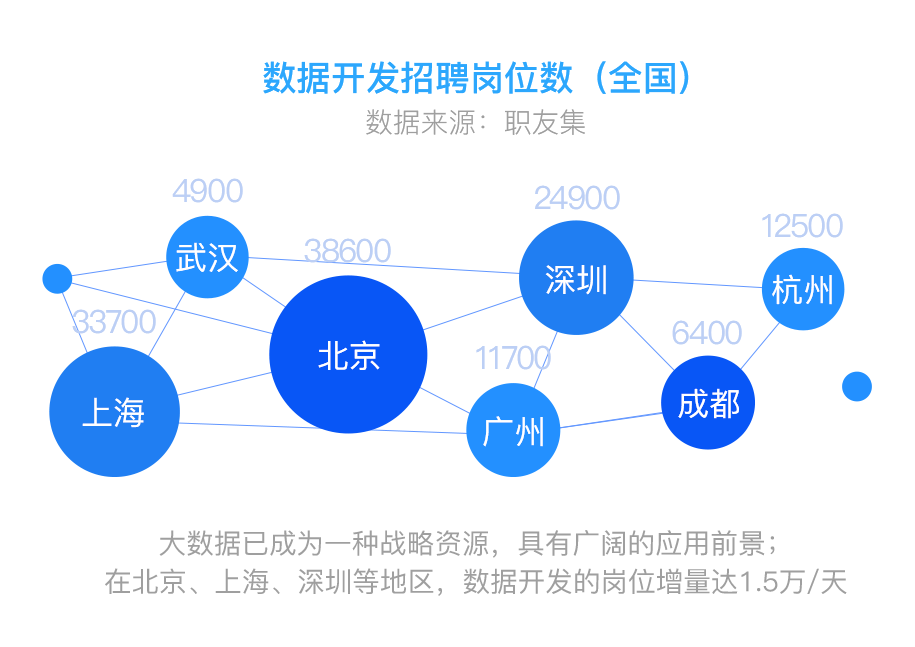
文章目录
- 对称锥规划:对称锥的增广拉格朗日乘子法(Semi-Smooth Newton Method解无约束优化子问题)
- 对称锥的增广拉格朗日函数
- Semi-Smooth Newton Method半光滑牛顿法
- 广义雅可比
- 半光滑性
- 半光滑牛顿算法
- 参考文献
对称锥规划:对称锥的增广拉格朗日乘子法(Semi-Smooth Newton Method解无约束优化子问题)
基础预备:
凸优化学习笔记(一)
约束优化:PHR-ALM 增广拉格朗日函数法
对称锥规划:锥与对称锥
对称锥的增广拉格朗日函数
从前面文章的分析中我们已经知道,对于一般优化问题,都可以使用PHR-ALM进行求解,那能否使用该方法求解对称锥规划问题呢?答案是否定的。因为在一般优化问题中,PHR-ALM中的增广项应该是凸且可微的,而对于锥规划的不等式约束,例如 K = Q n = { ( x 0 , x 1 ) T ∈ R × R n − 1 ∣ x 0 ≥ ∥ x 1 ∥ 2 } \mathcal{K}=\mathcal{Q}^n=\left\{\left(x_0, x_1\right)^{\mathrm{T}} \in \mathbb{R} \times \mathbb{R}^{n-1} \mid x_0 \geq\left\|x_1\right\|_2\right\} K=Qn={(x0,x1)T∈R×Rn−1∣x0≥∥x1∥2},若采用PHR-ALM直接构造 g ( x ) = ∥ x 1 ∥ 2 − x 0 ≤ 0 g(x)=\|x_1\|_2-x_0 \leq 0 g(x)=∥x1∥2−x0≤0,那么增广项 ∥ max [ g ( x ) , 0 ] ∥ 2 \left\|\max \left[g(x), 0\right]\right\|^2 ∥max[g(x),0]∥2是不可微的,会对无约束优化子问题的收敛速率和求解造成困难。

对于不等式约束 g ( x ) ≤ 0 g(x) \leq 0 g(x)≤0也即 A x + b ≤ 0 Ax+b \leq 0 Ax+b≤0而言,引入松弛变量 [ s ] 2 [s]^2 [s]2可将不等式约束转换成等式约束 A x + b + [ s ] 2 = 0 Ax+b+[s]^2=0 Ax+b+[s]2=0。利用该思想,换一种思路将不等式约束 A x + b ≤ 0 Ax+b \leq 0 Ax+b≤0写成 − A x − b ≥ 0 -Ax-b \geq 0 −Ax−b≥0,结合前面关于Nonnegative Orthant的理解, − A x − b ∈ K i = R ≥ 0 n -A x-b \in \mathcal{K}_i=\mathbb{R}_{\geq 0}^n −Ax−b∈Ki=R≥0n,可将普通的仿射不等式约束写成对称锥约束的形式。结合欧几里得若当代数可将对称锥写成一个平方操作,因此 R ≥ 0 n \mathbb{R}^n_{\geq 0} R≥0n 可用 { x 2 : = x ∘ x ∣ x ∈ R n } \left\{x^2:=x \circ x \mid x \in \mathbb{R}^n\right\} {x2:=x∘x∣x∈Rn}平方操作替代,故可引入松弛变量 [ s ] 2 [s]^2 [s]2将 R ≥ 0 n \mathbb{R}^n_{\geq 0} R≥0n写成等式约束。
核心思想是将对称锥约束写成广义不等式
A
i
x
+
b
i
∈
K
i
A_i x+b_i \in \mathcal{K}_i
Aix+bi∈Ki,并不需要将
K
i
\mathcal{K}_i
Ki进行显式表达:
min
x
∈
R
n
c
T
x
s.t.
A
i
x
+
b
i
∈
K
i
,
i
=
1
,
…
,
m
G
x
=
h
\begin{aligned} \min _{x \in \mathbb{R}^n} & \; c^{\mathrm{T}} x \\ \text { s.t. } & A_i x+b_i \in \mathcal{K}_i, i=1, \ldots, m \\ & G x=h \end{aligned}
x∈Rnmin s.t. cTxAix+bi∈Ki,i=1,…,mGx=h
直接引入
s
i
∘
s
i
∈
K
i
s_i \circ s_i \in \mathcal{K}_i
si∘si∈Ki将广义不等式写成等式形式:
min
x
,
s
c
T
x
s.t.
A
i
x
+
b
i
=
s
i
∘
s
i
,
i
=
1
,
…
,
m
G
x
=
h
\begin{array}{ll} \min _{x, s} & c^{\mathrm{T}} x \\ \text { s.t. } & A_i x+b_i=s_i \circ s_i, i=1, \ldots, m \\ & G x=h \end{array}
minx,s s.t. cTxAix+bi=si∘si,i=1,…,mGx=h
套PHR-ALM将对称锥约束的增广拉格朗日函数写为:
L
ρ
(
x
,
s
,
λ
,
ν
)
:
=
c
T
x
+
ρ
2
∥
G
x
−
h
+
λ
ρ
∥
2
+
ρ
2
∑
i
=
1
m
∥
A
i
x
+
b
i
−
s
i
∘
s
i
+
ν
i
ρ
∥
2
\mathcal{L}_\rho(x, s, \lambda, \nu):=c^{\mathrm{T}} x+\frac{\rho}{2}\left\|G x-h+\frac{\lambda}{\rho}\right\|^2+\frac{\rho}{2} \sum_{i=1}^m\left\|A_i x+b_i-s_i \circ s_i+\frac{\nu_i}{\rho}\right\|^2
Lρ(x,s,λ,ν):=cTx+2ρ
Gx−h+ρλ
2+2ρi=1∑m
Aix+bi−si∘si+ρνi
2
因为
min
x
,
s
L
ρ
(
x
,
s
,
λ
,
ν
)
=
min
x
min
s
L
ρ
(
x
,
s
,
λ
,
ν
)
\min _{x, s} \mathcal{L}_\rho(x, s, \lambda, \nu)= \min _{x} \min_s \mathcal{L}_\rho(x, s, \lambda, \nu)
minx,sLρ(x,s,λ,ν)=minxminsLρ(x,s,λ,ν),那么解无约束优化子问题的第一步就是解
min
s
L
ρ
(
x
,
s
,
λ
,
ν
)
\min_s \mathcal{L}_\rho(x, s, \lambda, \nu)
minsLρ(x,s,λ,ν)以消除引入的松弛变量
s
i
s_i
si:
min
s
L
ρ
(
x
,
s
,
λ
,
ν
)
=
c
T
x
+
ρ
2
∥
G
x
−
h
+
λ
ρ
∥
2
+
ρ
2
∑
i
=
1
m
min
s
i
∥
A
i
x
+
b
i
−
s
i
∘
s
i
+
ν
i
ρ
∥
2
\min _s \mathcal{L}_\rho(x, s, \lambda, \nu)=c^{\mathrm{T}} x+\frac{\rho}{2}\left\|G x-h+\frac{\lambda}{\rho}\right\|^2+\frac{\rho}{2} \sum_{i=1}^m \min _{s_i}\left\|A_i x+b_i-s_i \circ s_i+\frac{\nu_i}{\rho}\right\|^2
sminLρ(x,s,λ,ν)=cTx+2ρ
Gx−h+ρλ
2+2ρi=1∑msimin
Aix+bi−si∘si+ρνi
2
而核心是解
min
s
i
∥
A
i
x
+
b
i
−
s
i
∘
s
i
+
ν
i
ρ
∥
2
\min _{s_i}\left\|A_i x+b_i-s_i \circ s_i+\frac{\nu_i}{\rho}\right\|^2
minsi
Aix+bi−si∘si+ρνi
2。令
v
=
A
i
x
+
b
i
+
ν
i
ρ
v=A_i x+b_i+\frac{\nu_i}{\rho}
v=Aix+bi+ρνi,则
min
s
∥
v
−
s
i
∘
s
i
∥
2
=
min
x
∈
K
∥
v
−
x
∥
2
\min _s\left\|v-s_i \circ s_i\right\|^2=\min _{x \in \mathcal{K}}\|v-x\|^2
mins∥v−si∘si∥2=minx∈K∥v−x∥2,这就是一个正交投影(最佳逼近)问题,在对称锥约束
K
\mathcal{K}
K中找到一个
x
x
x使得
v
v
v和
x
x
x之间的距离最短,而最优的
x
x
x就是
v
v
v在锥
K
\mathcal{K}
K上的投影,将其写为:
P
K
(
v
)
:
=
arg
min
x
∈
K
∥
v
−
x
∥
2
P_{\mathcal{K}}(v):=\arg \min _{x \in \mathcal{K}}\|v-x\|^2
PK(v):=argminx∈K∥v−x∥2。如下图所示,利用对称锥的谱分解可求出
v
v
v在锥
K
\mathcal{K}
K上的投影:
P
K
(
v
=
∑
i
=
1
θ
λ
i
q
i
)
=
∑
i
=
1
θ
max
[
λ
i
,
0
]
q
i
P_{\mathcal{K}}\left(v=\sum_{i=1}^\theta \lambda_i q_i\right)=\sum_{i=1}^\theta \max \left[\lambda_i, 0\right] q_i
PK(v=i=1∑θλiqi)=i=1∑θmax[λi,0]qi
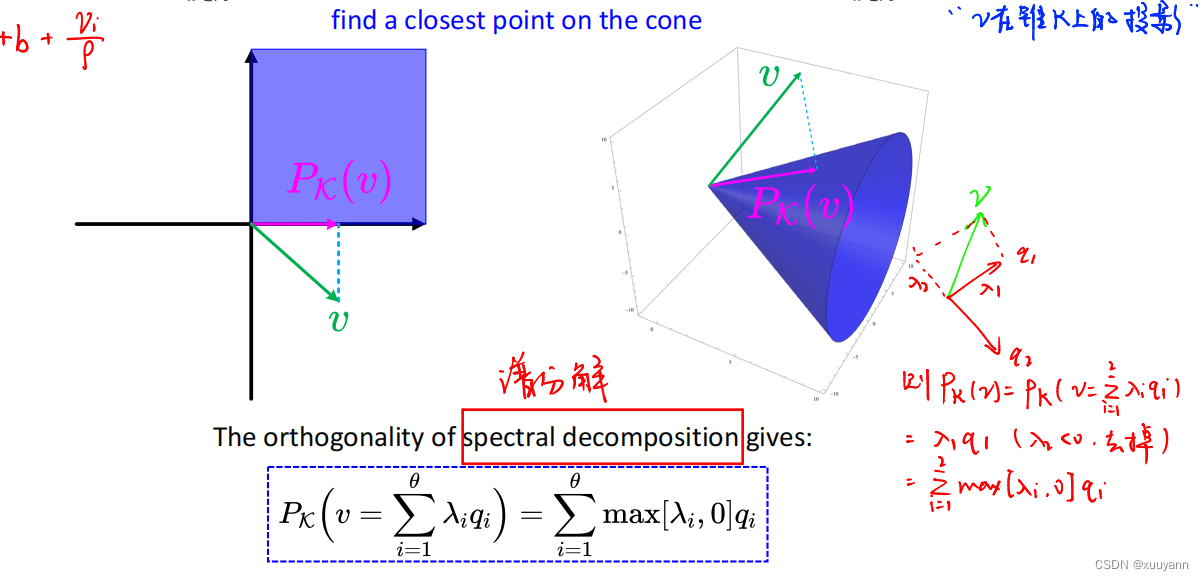
对于Nonnegative Orthant和SOCP,利用谱分解求锥上的投影:

利用显式投影算子,我们可以得到:
min
s
∥
v
−
s
i
∘
s
i
∥
2
=
∥
v
−
P
K
(
v
)
∥
2
\min _s\left\|v-s_i \circ s_i\right\|^2=\left\|v-P_{\mathcal{K}}(v)\right\|^2
smin∥v−si∘si∥2=∥v−PK(v)∥2
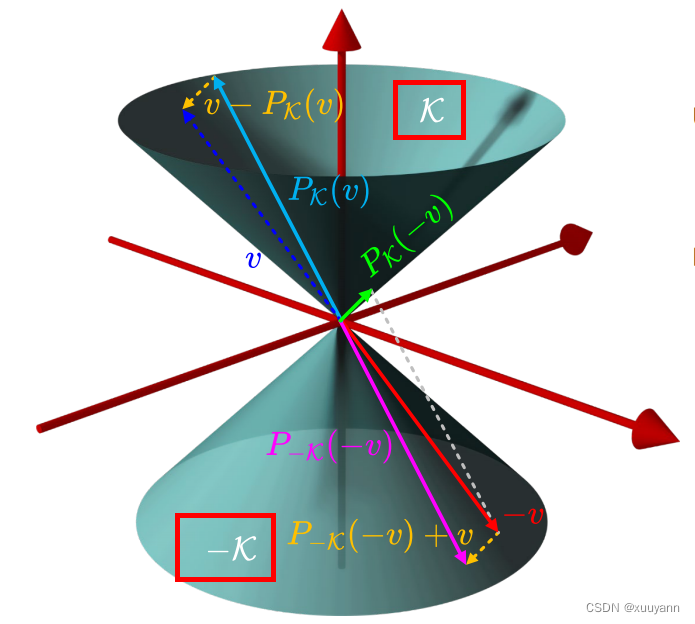
如下图所示,黄色虚线向量表示
v
−
P
K
(
v
)
v-P_{\mathcal{K}}(v)
v−PK(v),且
v
−
P
K
(
v
)
⊥
P
K
(
v
)
v-P_{\mathcal{K}}(v) \bot P_{\mathcal{K}}(v)
v−PK(v)⊥PK(v),根据对称性有
v
−
P
K
(
v
)
=
−
[
−
v
−
P
−
K
(
−
v
)
]
=
v
+
P
−
K
(
−
v
)
v-P_{\mathcal{K}}(v)=-[-v-P_{\mathcal{-K}}(-v)]=v+P_{\mathcal{-K}}(-v)
v−PK(v)=−[−v−P−K(−v)]=v+P−K(−v),其中
P
−
K
(
−
v
)
P_{\mathcal{-K}}(-v)
P−K(−v)表示
−
v
-v
−v投影到
−
K
\mathcal{-K}
−K上。又将
−
v
-v
−v投影到锥
K
\mathcal{K}
K上可得到绿色实线向量
P
K
(
−
v
)
P_{\mathcal{K}}(-v)
PK(−v),此时灰色虚线、黄色虚线、粉红实线和绿色实线构成了一个长方形,因此
P
K
(
−
v
)
=
v
+
P
−
K
(
−
v
)
P_{\mathcal{K}}(-v)=v+P_{\mathcal{-K}}(-v)
PK(−v)=v+P−K(−v),由此推出
v
−
P
K
(
v
)
=
P
K
(
−
v
)
v-P_{\mathcal{K}}(v)=P_{\mathcal{K}}(-v)
v−PK(v)=PK(−v),这样我们可以得到更为简洁的形式:
min
s
∥
v
−
s
i
∘
s
i
∥
2
=
∥
P
K
(
−
v
)
∥
2
\min _s\left\|v-s_i \circ s_i\right\|^2=\left\|P_{\mathcal{K}}(-v)\right\|^2
smin∥v−si∘si∥2=∥PK(−v)∥2
将上式带入原对称锥的增广拉格朗日函数中,可得到:
min
s
L
ρ
(
x
,
s
,
λ
,
ν
)
=
c
T
x
+
ρ
2
∥
G
x
−
h
+
λ
ρ
∥
2
+
ρ
2
∑
i
=
1
m
∥
P
K
i
(
−
A
i
x
−
b
i
−
ν
i
ρ
)
∥
2
\min _s \mathcal{L}_\rho(x, s, \lambda, \nu)=c^{\mathrm{T}} x+\frac{\rho}{2}\left\|G x-h+\frac{\lambda}{\rho}\right\|^2+\frac{\rho}{2} \sum_{i=1}^m\left\|P_{\mathcal{K}_i}\left(-A_i x-b_i-\frac{\nu_i}{\rho}\right)\right\|^2
sminLρ(x,s,λ,ν)=cTx+2ρ
Gx−h+ρλ
2+2ρi=1∑m
PKi(−Aix−bi−ρνi)
2
可看出最小化后的增广拉格朗日函数与松弛变量
s
i
s_i
si无关。为了表达上的便捷性,我们令
μ
=
−
ν
\mu=-\nu
μ=−ν,最终可得推导得到与上式等价的对称锥增广拉格朗日函数为:
L
ρ
(
x
,
λ
,
μ
)
:
=
c
T
x
+
ρ
2
{
∥
G
x
−
h
+
λ
ρ
∥
2
+
∑
i
=
1
m
∥
P
K
i
(
μ
i
ρ
−
A
i
x
−
b
i
)
∥
2
}
\mathcal{L}_\rho(x, \lambda, \mu):=c^{\mathrm{T}} x+\frac{\rho}{2}\left\{\left\|G x-h+\frac{\lambda}{\rho}\right\|^2+\sum_{i=1}^m\left\|P_{\mathcal{K}_i}\left(\frac{\mu_i}{\rho}-A_i x-b_i\right)\right\|^2\right\}
Lρ(x,λ,μ):=cTx+2ρ{
Gx−h+ρλ
2+i=1∑m
PKi(ρμi−Aix−bi)
2}
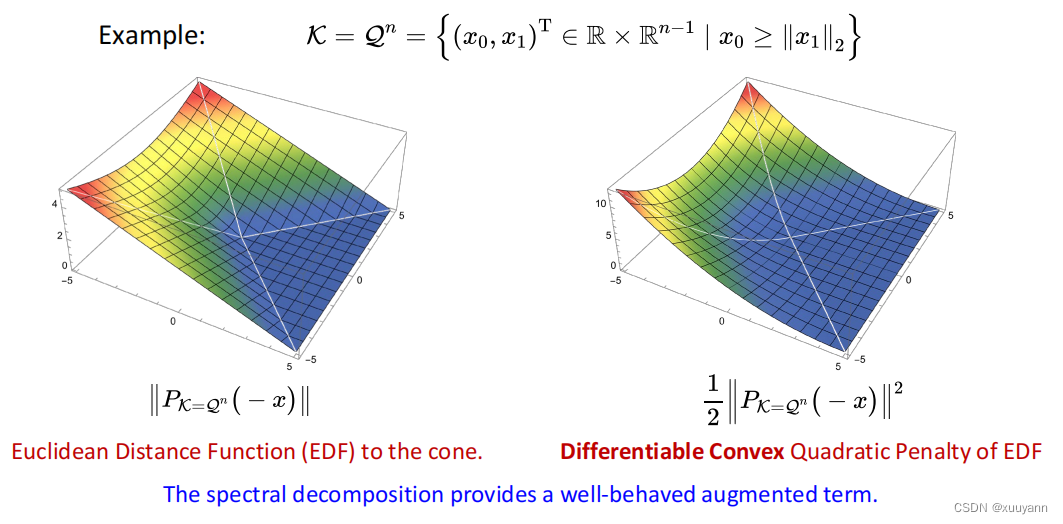
对该函数的增广项进行分析,令
ρ
=
1
,
μ
=
0
,
b
=
0
,
A
=
I
\rho=1,\mu=0,b=0,A=I
ρ=1,μ=0,b=0,A=I,则
ρ
2
∥
P
K
(
μ
ρ
−
A
x
−
b
)
∥
2
=
1
2
∥
P
K
(
−
x
)
∥
2
=
1
2
∥
x
−
P
K
(
x
)
∥
2
\frac{\rho}{2}\left\|P_{\mathcal{K}}\left(\frac{\mu}{\rho}-A x-b\right)\right\|^2=\frac{1}{2}\left\|P_{\mathcal{K}}(-x)\right\|^2=\frac{1}{2}\left\|x-P_{\mathcal{K}}(x)\right\|^2
2ρ
PK(ρμ−Ax−b)
2=21∥PK(−x)∥2=21∥x−PK(x)∥2,该惩罚项实际上惩罚的是
x
x
x到锥
K
\mathcal{K}
K的欧氏距离的平方,是可微且凸的,如下图所示。综上所述,相比于直接构造
g
(
x
)
=
∥
x
1
∥
2
−
x
0
≤
0
g(x)=\|x_1\|_2-x_0 \leq 0
g(x)=∥x1∥2−x0≤0的方式,利用对称锥的欧几里得若当代数和谱分解性质可以提供一个可微且凸的增广项,降低了后续无约束优化子问题的求解难度。
算法迭代过程中的参数更新和终止条件如下图所示,其中内层无约束优化子问题的终止条件与一般优化问题的PHR-ALM一样。

Semi-Smooth Newton Method半光滑牛顿法
对称锥的ALM算法第一步就是求解一个无约束优化子问题 argmin x L ρ ( x , λ , μ ) \operatorname{argmin}_x \mathcal{L}_\rho(x, \lambda, \mu) argminxLρ(x,λ,μ),从前面的分析已知 L ρ ( x , λ , μ ) \mathcal{L}_\rho(x, \lambda, \mu) Lρ(x,λ,μ)凸且一阶可微但二阶不连续(梯度函数分片连续但边界处不连续),如下图所示。该函数的Hessian矩阵只能在梯度分片连续的地方求解出来,在不连续的边界处无法求解。使用一些一阶算法(梯度下降、拟牛顿法等)也可以,但收敛到高精度解往往很慢。要想更快的收敛速度,可以考虑牛顿方法,但牛顿方法要求Hessian矩阵存在且无法保证全局收敛性。在这里,针对不可微问题,我们引入具有全局收敛性的半光滑牛顿法(Semi-Smooth Newton Method)。

广义雅可比


半光滑性


半光滑牛顿算法
半光滑性可保证牛顿型算法在迭代过程中具有局部超线性收敛(local superlinear convergence)或者局部二次收敛(local quadratic convergence)。对称锥增广拉格朗日的梯度是分段C2的,因此它是强半光滑的,通过对 H ∈ ∂ B ∇ x L ρ ( x , λ , ρ ) H \in \partial_B \nabla_x \mathcal{L}_\rho(x, \lambda, \rho) H∈∂B∇xLρ(x,λ,ρ)进行微小摄动保证正定性,我们可以计算出下面的半光滑牛顿步长 d d d来进行无约束优化。


参考文献
机器人中的数值优化
最优化:建模、算法与理论/最优化计算方法