0与1的世界

计算机是由晶体管和电路板组成的电子设备。

不论是我们微信信息的呈现、图像的储存和数字之间的运算本质上都是0和1的信息。

0、1便可以代表电压的高低、开关的闭合以及电阻的导电和不导电。 0、1表示的数字便是“逢二进一”。计算机的最小的储存单位是位（bit），其上能存储0或者1。8位（bit）等于1字节（Byte）,是计算机中的数据的基本单位。

最初计算机被设计表示的时候，26个英文字母和10个数字，在加上一些符号，最接近2的7次方128，为了留取容错便设定为8位表示，也就是8位（bit）等于1字节（Byte）的由来。

我便以1个字节来演示：
为了方便计算，计算机给数字延申了不同形式的存储，原码和补码以及反码。一共8位，最初的一位代表数字的正负，0代表正数，1是负数。

数字	原码	反码	补码
1	0000 0001	0000 0001	0000 0001
3	0000 0011	0000 0011	0000 0011
7	0000 0111	0000 0111	0000 0111
-3	1000 0011	1111 1100	1111 1101
-5	1000 0101	1111 1010	1111 1011

原码

原码是最便于理解的，8位的能表示的数字范围便是[-127,127]之间，虽然我们很好理解，但对于机器来说原码不能用于计算。如果出现负数便无法计算。

1 + 3 = 0000 0001 + 0000 0011 = 0000 0100 = 4
1 - 3 = 1 + （-3）= 0000 0001 + 1000 0011 = 1000 0100 = -4

反码

正数是其本身，负数是在正数的基础上各个位置取反，符号位还是1。因为0不区分正负所以反码依然满足不了计算机用于计算。

1 - 3 = 1 + （-3）= 0000 0001 + 1000 0011（原码） = 0000 0001 + 1111 1100（反码）= 1111 1101 （反码）= 1000 0010 （原码）= -2
1 - 1 = 1 + （-1）= 0000 0001 + 1000 0001（原码） = 0000 0001 + 1111 1110（反码）= 1111 1111 （反码）= 1000 0000 （原码）= -0

补码

正数是其本身，负数是在正数的基础上各个位置取反后+1，符号位还是1。

1 - 3 = 1 + （-3）= 0000 0001 + 1000 0011（原码） = 0000 0001 + 1111 1101（补码）= 1111 1110 （补码）= 1000 0010 （原码）= -2
1 - 1 = 1 + （-1）= 0000 0001 + 1000 0001（原码） = 0000 0001 + 1111 1111（补码）= 0000 0000 （补码）= 1000 0000 （原码）= 0

位移运算

>> << 这是左右位移的计算，尖括号向那边就是向那里平移，带符号位，负数向右移动，最高位补1；>>> 这个是不带符号位位移，下面的例子中位移之后按照补码计算。<<< 不存在无符号的移动

数字	原码	补码	>>1	<<1	>>2	<<2	>>>1
1	0000 0001	0000 0001	0000 0000(0)	0000 010(2)	0000 0000(0)	0000 0100(4)	0000 0000(0)
3	0000 0011	0000 0011	0000 0001(1)	0000 0110(6)	0000 0000(0)	0000 1100(12)	0000 0001(1)
-1	1000 0001	1111 1111	11111 1111(-1)	1111 1110(-2)	11111 1111(-1)	1111 1100(-4)	0111 1111(127)
-3	1000 0011	1111 1101	1111 1110(-2)	1111 1010(-6)	1111 1111(-1)	1111 0100(-12)	0111 1110(126)

位与&、位或|、按位异或^、按位取反~

位与是二者都为1才为1；位或其中一个为1则为1；按位取反~，字面意思数字取反；按位异或^ 数字相同为0，不同为1

浮点数

计算机定义了两种小数，定点数和浮点数，定点数是小数位数和小数点固定的数字，这里我以27.8125这个小数点在计算机的储存为例子。

整数为26，二进制对应的是11011
小数部分为0.8125，计算小数的去乘以2，有1取1，否则为0，直到所有的数字为0，就是1101
合计来就是11011.1101

在java中如何储存浮点数呢？采用的科学计数法表示的。以double为例子，double是双精度浮点数，内存占8个字节，共64位，有效位数位15位。储存形式如下：

• 符号位 0
• 阶码位 E= e + (2^(n-1) -1) 11011.1101 = 1.10111101 * 10^4 ,此处可得到4 + (2^(n-1) -1) = 4 +1024 -1 = 1027。1027对应的2进制的数字位
• 位数是1.10111101 忽略小数点和第一个1就是10111101

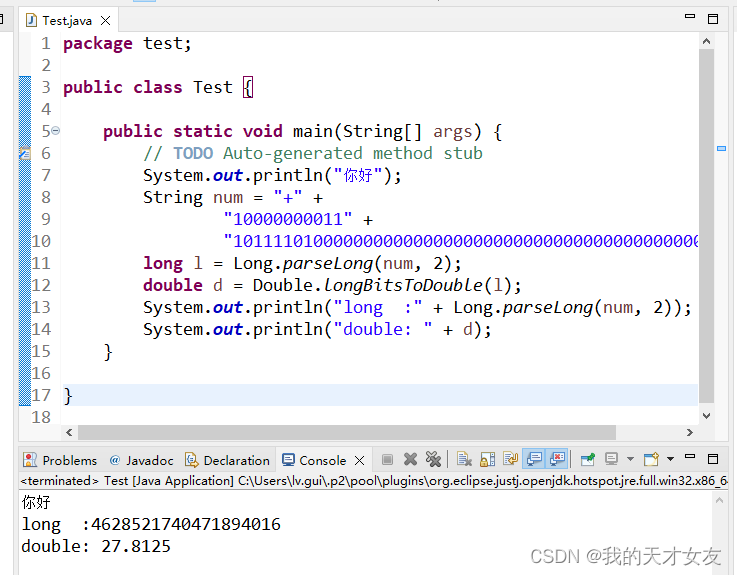
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		System.out.println("你好");
		String num = "+" +
				"10000000011" + 
				"1011110100000000000000000000000000000000000000000000";
		long l = Long.parseLong(num, 2);
		double d = Double.longBitsToDouble(l);
		System.out.println("long  :" + Long.parseLong(num, 2));
		System.out.println("double: " + d);
	}

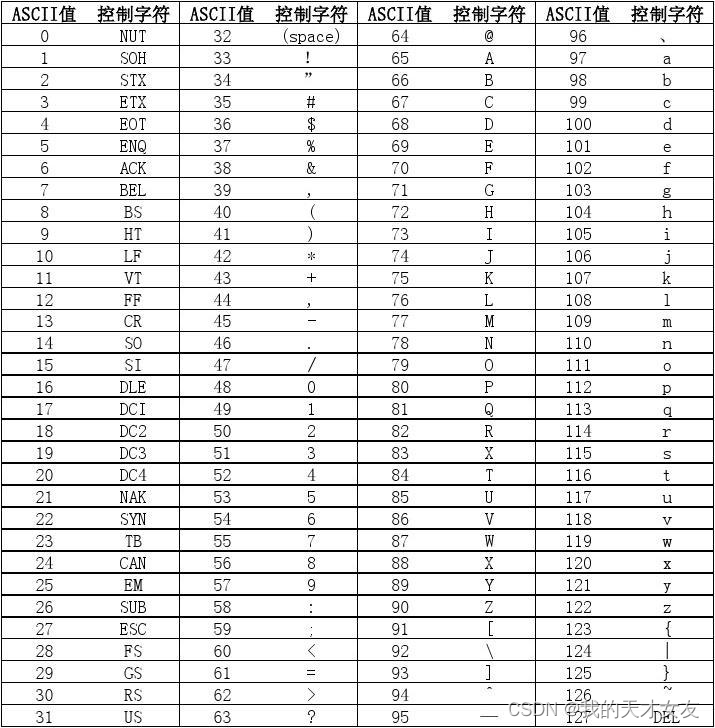
编码格式

比较常见的编码格式：ASCII、Unicode、GBK等，ASCII码使用一字节8bit来表示，一共128个字符，第一位固定使用0显示。还制作了全世界通用的编码 unicode，UTF-8、UTF-16、UTF-32都是不同程度压缩的unicode编码。最常见的UTF-8，一个汉字使用三个字节表示。实际编程中需要注意编码不同带来的乱码。

CPU

cpu是电脑的核心部件，是一块集成电路板，工艺级别在纳米，主要由基板、核心和针脚组成。基板是用来固定核心和针脚的，针脚通过基板上的基座连接电流信号。

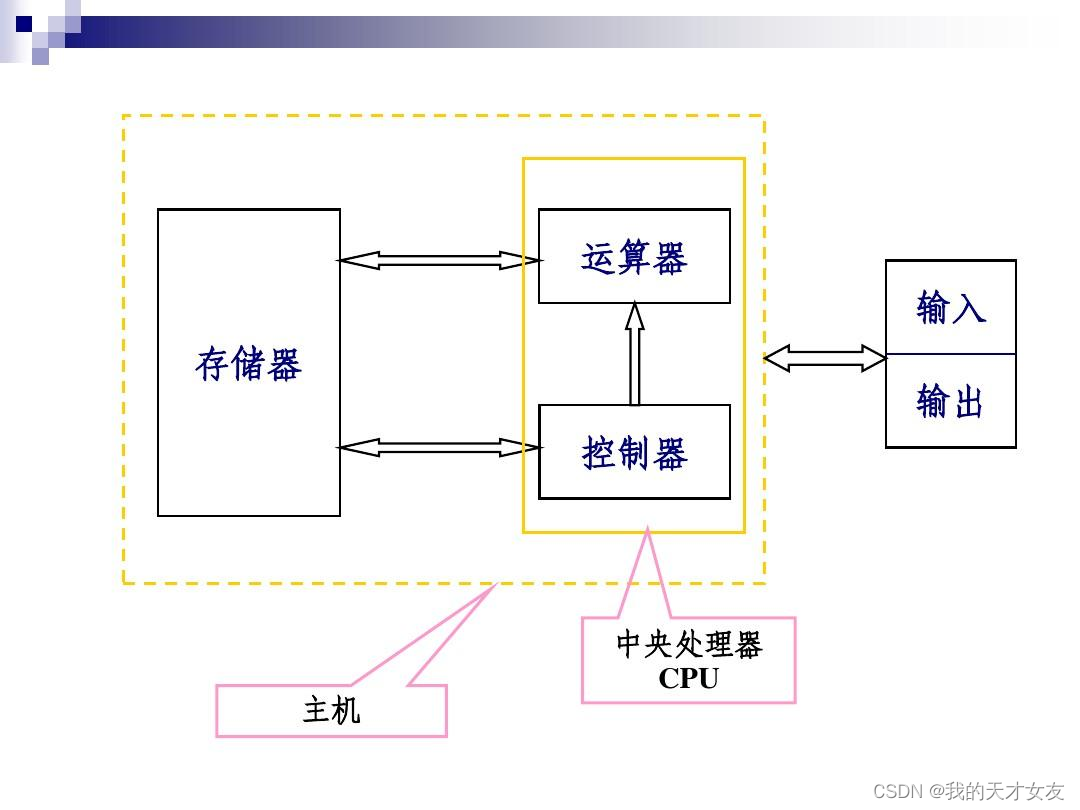
控制器是CPU的核心，控制器读取存储器（寄存器）中的数据，通过运算器计算将结果储存在存储器中，目前cpu及其运算能力远大于读取内存的速度，越接近cpu读取的数据就会越快，位于cpu中L1、L2高速缓存是最接近CPU的，因此尤为重要。

TCP/IP

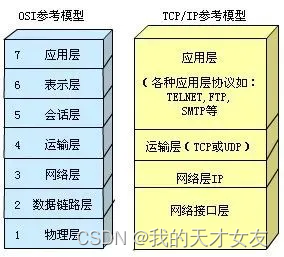
TCP是网络中传输层，IP是网络层，通过IP地址32位4个字节代表地址。类似与TCP是快递分发的，ip是具体配送的。